使用变换工具，可对几何体进行平移、旋转或缩放。Step1.在操控板中按下“变换”按钮，操控板进入图5.1.3所示的“变换”操作界面，同时图形区中的模型周围出现图5.1.4所示的控制杆和背景对罩框。一维缩放：将鼠标指针移至边线上的边控制滑块时，立即显示图5.1.6b所示的操作手柄，若只拖动图5.1.6b中的操作手柄的某个箭头，则相对于该边的对边进行一维缩放。图5.1.6 “缩放”操作......
2023-06-20
数论变换：简单高效的数学处理方法
【摘要】：与余弦变换基相比，数论变换没有舍入误差，不需要存储三角函数，在相同变换长度下，速度优于余弦变换。而且数论变换本身就是整型变换，无需进行提升就可得到可逆的变换。对比式和式可以看出，反数论变换基中的元素β=α-1，又α-1=αN-1，所以反数论变换基如下：实现构造数论变换MATLAB代码如下：实现构造数论变换MATLAB代码如下：4阶数论变换基函数图形如图4-5所示。图4-54 阶数论变换基函数图形图4-54 阶数论变换基函数图形
20世纪70年代初，Rader和Agarwal及Burrus等人提出了构造模M剩余类环ZM上的离散变换，即数论变换（Number Theoretic Transform），并把数论变换引入数字信号处理中。与余弦变换基相比，数论变换没有舍入误差，不需要存储三角函数，在相同变换长度下，速度优于余弦变换。而且数论变换本身就是整型变换，无需进行提升就可得到可逆的变换。
数论变换是在以正整数M为模的整数环ZM上定义的线形正交变换，所用运算法则是数论中同余运算，它在ZM上具有循环卷积特性，基本函数由整数的方幂构成。设xi∈ZM，i=0，1，…，N-1，如果作用在序列x0，x1，xN-1上的一种变换为
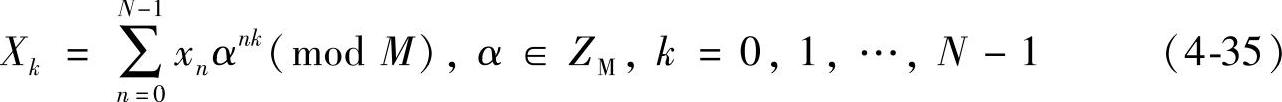
有如下形式的逆变换：
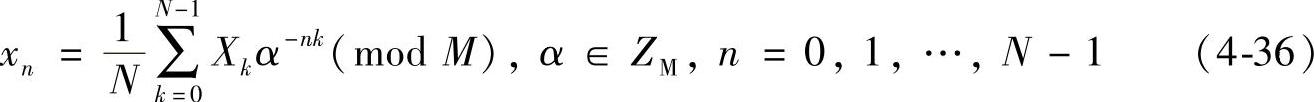
且具有循环卷积性质，则称式（4-35）为在ZM上长为N的数论变换，可表示成：
X≡T·x（mod M） （4-37）
式中，T是数论变换基，形式如下：
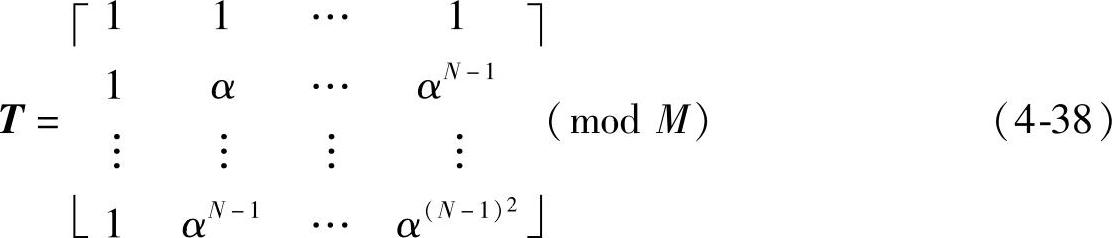
式（4-37）中，x=[x0，x1，…，xN-1]T，xn∈ZM（n=0，1，…，N-1）且α∈ZM。以上两式各元素选取的条件有：①M是质数；②N必须是M-1的因子；③α是模M的N阶单位根，即αN=1（mod M），且αk≠1（mod M）（k=1，2，…，N-1）。
对比式（4-35）和式（4-36）可以看出，反数论变换基中的元素β=α-1，又α-1（mod M）=αN-1（mod M），所以反数论变换基如下：
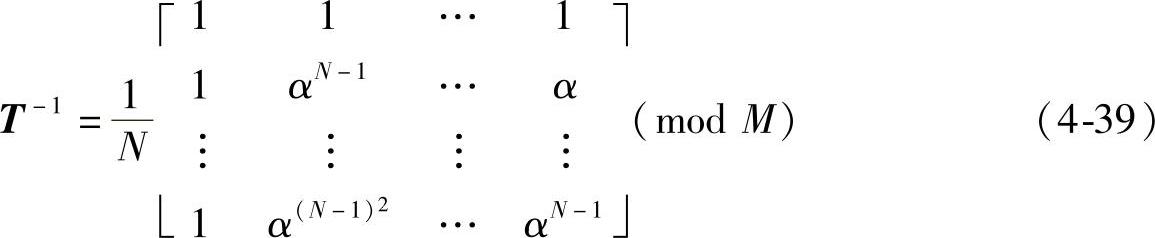
实现构造数论变换MATLAB代码如下：
4阶数论变换（M=5，α=2）基函数图形如图4-5所示。
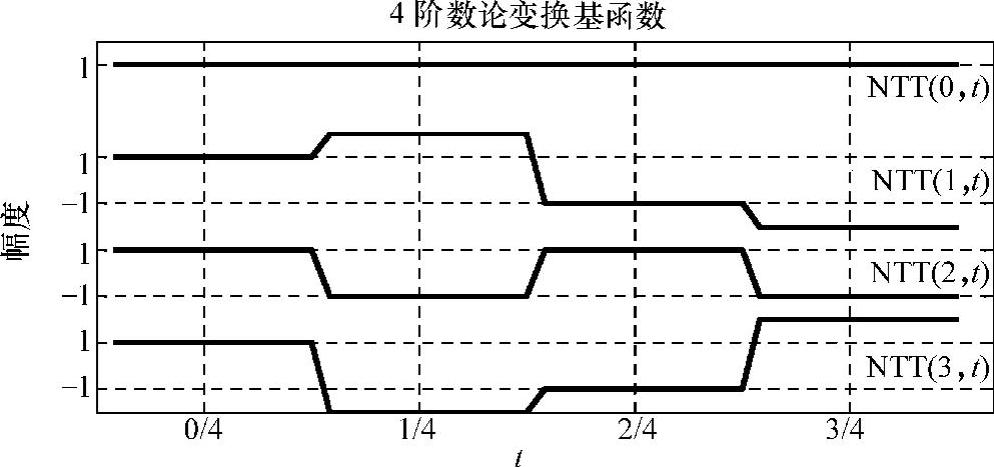
图4-54 阶数论变换基函数图形
有关全相位数字信号处理方法及MATLAB实现的文章
- 详细阅读
-
极聪明数学图解，点亮数学的简单方法详细阅读
也许，成为一个数意味着成为一个能够进行运算的系统的一部分。环是一类涵盖范围很广的具有某种结构的集合，它配有两个二元运算，它们与我们一般对数进行的加法和乘法运算很类似。其中一个运算构成一个交换群，被看作“加法”。另外一个运算只需要拥有一个单位元，并对前一个运算有分配律，这个运算是“乘法”。这从直观上意味着，除法也可以作为域上的运算。......
2023-11-22
-
如何练习吉他和弦转换？简单高效方法分享！详细阅读
很多人练习和弦转换时会觉得很难，练了很久都不熟练。下面介绍一下练习和弦转换的方法：第一，从简单的和弦开始。Dm—G7和弦的转换：从Dm和弦转换到G7和弦比较容易，难的是Dm和弦比较难按，所以先好好练习Dm，然后保留食指不动，挪动中指和无名指按上G7即可。C—G7和弦的转换：C和弦的食指和中指、无名指向外扩张，按上G7和弦；G7和弦向内收，是C和弦。......
2023-11-20
-
印度验算法：简单、高效、准确详细阅读
我们平时进行验算时，往往是重新计算一遍，看结果是否与上一次的结果相同。这相当于用两倍的时间来计算一个题目。而印度的验算法相当简单，首先我们需要定义一个方法N，它的目的是将一个多位数转化为一个个位数。有了这个定义，我们就能对加减乘法进行验算了。练习验算88＋26=114验算94＋63=157验算105-26=79验算6675-526=6149验算97×16=1552验算37×77=2849......
2023-10-27
- 详细阅读
-
坐标变换的数学基础探究详细阅读
若采用磁势分布和功率不变的绝对变换，三相交流电流在空间产生的磁势F与二相交流电流产生的磁势应该相等。设变换矩阵为C3/2，则图2-9 abc坐标系与αβ坐标系如图2-9所示，假设αβ直角坐标系下的轴上绕组匝数为1，而abc坐标系下，各轴上的绕组匝数为k，则按照变换前后磁势不变有而αβ0坐标系统下的β轴电流为由式和式得......
2023-06-23
-
强夯法：设备简单、速度快、低成本的地基处理方详细阅读
强夯法具有设备简单、施工速度快、不添加特殊材料、造价低、适应处理的土质类别多等特点，目前强夯法已成为我国最常用的地基处理方法之一。此外，对于饱和软黏土，如淤泥和淤泥质地基，强夯处理效果不显著，目前一般谨慎采用。由于建筑物基础的应力扩散作用，强夯处理的范围应大于建筑物基础范围，具体扩大范围可根据建筑结构类型和重要性等因素综合考虑确定。......
2023-11-07
-
奇偶校验：简单，高效，字符级检错详细阅读
奇偶校验是一种古老而简单的差错检测方法。按照此规则编成的校验码，分别称为奇校验码或偶校验码。因此，奇偶校验的检错概率只有50%。垂直奇偶校验可以校验单个字符的错，因而又称为字符奇偶校验。例如，有一个字符，其编码为1010101，则这个字符的奇校验码为10101011，偶校验码为10101010。水平奇偶校验的检测能力强，但实现起来相对复杂。图2.21 表明了水平垂直奇偶校验各信息码元与校验码元之间的关系。......
2023-10-19
相关推荐