沃尔什基矩阵与一维变换时相同，由沃尔什函数产生。由沃尔什矩阵可以构成二维沃尔什函数的基本图像。表5-24 阶沃尔什基本图像矩阵与傅里叶基本图像不同的是，沃尔什变换等其他正交变换基图像均是实矩阵。二维哈达玛变换基矩阵与沃尔什基矩阵只是行向量排列顺序不同，正反变换形式相同。......
2023-06-23
哈达玛变换：理论与应用
【摘要】：在数字信号处理中，为了可进行快速运算，取样数通常取2的整数次幂，因而沃尔什变换和哈达玛变换这两种称呼常被混用。有时，这两类变换被统称为沃尔什-哈达玛变换。哈达玛变换基具有简单的递推关系，给计算带来很大方便。按照式生成哈达玛矩阵的MATLAB代码如下：N=4时运行结果如图4-4所示。2阶哈达玛变换基等于：式中，表示克罗内克直积。所以，反变换哈达玛基等于正变换哈达玛基。
由上面分析可知，离散沃尔什变换是对[0，1]区间上的连续沃尔什函数进行等间隔取样的结果，因为沃尔什函数是一组完备正交函数集，故可用于正交变换。从本质上说，哈达玛变换与沃尔什变换是相同的，它们的区别在于当取样数N是2的整数幂时，这两类变换基仅仅是行（列）的顺序不同；当N不是2的整数幂时，沃尔什变换可用于任意正整数，而哈达玛变换仅能用到N=200。在数字信号处理中，为了可进行快速运算，取样数通常取2的整数次幂，因而沃尔什变换和哈达玛变换这两种称呼常被混用。有时，这两类变换被统称为沃尔什-哈达玛变换。哈达玛变换基具有简单的递推关系，给计算带来很大方便。一维哈达玛正变换核由下列公式给出：
a（i，j）=（1/N）（-1）p（i，j），i，j=0，1，2，…，N-1 （4-31）
式中
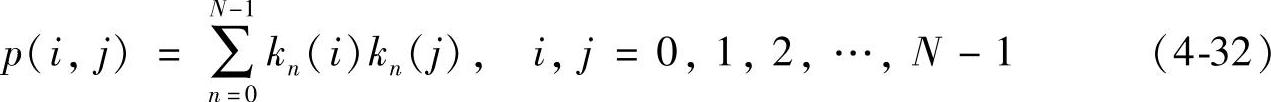
需注意的是，式（4-32）中符号∑表示模2加法，kn（i）表示数z的二进制表示中第i个比特值。按照式（4-31）生成哈达玛矩阵的MATLAB代码如下：
N=4时运行结果如图4-4所示。MATLAB定义的哈达玛内联函数是hard- mard（n）。当N=2n（n为整数）的哈达玛变换基可通过下面递推公式求得：
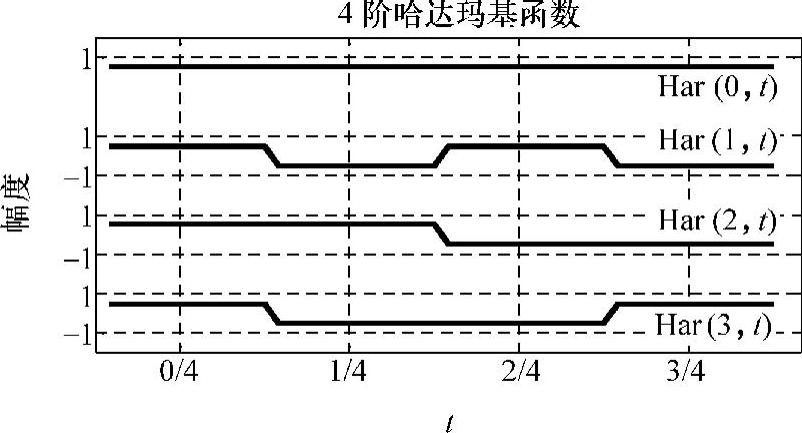
图4-4 4阶哈达玛基函数
式中，
表示克罗内克（Kronecker）直积。2阶哈达玛变换基等于：
采用式（4-33）生成哈达玛变换基的MATLAB代码如下：
结合式（4-33）和式（4-34）易知哈达玛基是正交基；又由式（4-32）可知哈达玛基具有对称性。所以，反变换哈达玛基等于正变换哈达玛基。
有关全相位数字信号处理方法及MATLAB实现的文章
- 详细阅读
-
理论与实践：1/K内插模板设计在正交变换下的详细阅读
假设输入图像大小为N×N，则在某正交变换对α和β下1/K内插模板设计过程如下：1）写出1/K单位抽取算子d，d中只有N2/K个元素为1而其余为0。离散沃尔什变换简单、直观，其正交基只有两种状态，用它来表示图像的物理性质较为清楚，因此用沃尔什变换设计的各种图像处理模板系数都是有理数，且规则性强、易于归纳总结。用离散傅里叶变换设计的模板系数是无理数，但它却有明确的物理意义。......
2023-06-23
-
光矢量变换与复频谱色度理论解析详细阅读
不同色光相加不是在能量层级上相加，在复频谱上是它们的色矢量相加。人眼虽然看不见色矢量，我们可以把一个准单色光的能量、微弧度及色矢量映射在复频谱图上。虽然微弧度Δθ很窄，可是它里面众多的色矢量分别处在以r为中心均等对称的相位上，这些色矢量在自发地合成中心色矢量r时，在色矢量r的垂直方向又合成出两个大小相等但是方向相反的分色矢量。很显然，这些分色矢量会自发地互相平衡。......
2023-11-18
-
光矢量变换色度理论解析详细阅读
波长长于780nm的电磁辐射称红外线；波长短于380nm的电磁辐射叫紫外线。光与色相比，不妨把白光看作载波，物体对白光选择性吸收，使白光的振幅发生变化，看作对白光振幅的调制。流明则由标准单位坎德拉引出。人眼对颜色的辨别主要是依靠锥体细胞，它们主要分布在视网膜中心凹部位。可是随着光照强度的减弱，锥体细胞辨别颜色的能力也随之下降。大量的科学实验表明，必须有足够大数量的光子数同时落在1个锥体细胞上，才能产生颜色视觉。......
2023-11-18
-
半桥变换电路设计与应用详细阅读
半桥变换电路的原理如图4.15 所示，工作波形如图4.16 所示。图4.15半桥电路原理图在半桥电路中，S1 与S2 交替导通，使变压器一次侧形成幅值为Ui/2 的交流电压。当滤波电感L 的电流连续时，输出电压为图4.16半桥电路的理想化波形当输出电感电流不连续，输出电压Uo 将高于式的计算值，并随负载减小而升高。在负载为零的极限情况下，半桥变换电路变压器利用率高，且没有偏磁问题，所以广泛用于数百W 至kW 的开关电源中。......
2023-06-23
-
电阻等效变换原理与应用技巧详细阅读
如果我们把虚线框内的5个电阻从A、B两点断开，求这个无源二端网络的 “等效”电阻RAB，即若Y形电阻网络中3个电阻值相等，则等效△形电阻网络中3个电阻也相等，即图1.15电阻之间的等效变换于是，5个电阻就由RAB来替代了，替代以后，并不改变待求量I和U，所以我们说RAB是虚线框内电路部分的“等效”电阻。Y形电阻网络与△形电阻网络之间的等效变换，除了计算电路的入端电阻以外，还能较方便地解决实际电路中的一些其他问题。......
2023-06-24
-
光矢量变换与白平衡理论解析详细阅读
复频谱理论认为，能量是标量，三个准单色光相加后呈现的白平衡，并不是在能量层级上实现的平衡，而是由三个准单色光隐含的色矢量r相加实现的平衡。三基色色矢量在复频谱图上的相位是固定的，正如图6-1所示。实际上是绿色矢量rg与蓝色矢量rb共同合成一个色矢量rp，这个rp与红色矢量rr大小相等，但方向相反，从而实现了三基色的色矢量白平衡。......
2023-11-18
-
直流变换电路设计与应用详细阅读
直流-直流变换电路主要以全控型器件作为电路主开关器件，开关频率越高，斩波电路输出电压纹波越小，滤波越容易，电力公害越小。近年来，电力电子器件及控制技术的迅速发展也极大地促进了直流变换技术的发展，各种新型斩波电路不断出现，为进一步提高直流变换电路的动态性能、降低开关损耗、减小电磁干扰开辟了新途径。直流-直流变换电路的拓扑结构种类较多，根据输入输出是否隔离可分为非隔离型斩波电路和隔离型斩波电路。......
2023-06-23
相关推荐