首页理论教育余弦正交基简介及在音视频压缩中的应用

余弦正交基简介及在音视频压缩中的应用

2023-06-23 理论教育版权反馈

【摘要】：对于长度为N的一维信号X，余弦变换定义TC为TC=CN·X 正弦正交基元素由下列函数生成：由式确定的变换称为离散余弦变换。可通过近似为整数后变换，称为整数DCT，在H.264及AVS标准中被使用。对于4阶DCT，余弦变换基等于：式中，c=2cos（π/8）和s=sin（π/8）。余弦变换主要应用在数据内插、图像压缩方面，在MPEG-2、H.264、AVS等音视频压缩标准中得到了广泛应用。

设f（x），x=0，1，2，…，N-1，为离散序列，按照下式延拓成偶对称序列f_s（x）：

f_s（x+1/2）=f（x）且f（x）=f（-x-1）（4-18）

式中，x∈[-N，N-1]。显然f_s关于x=-1/2偶对称，如图4-2所示。

图4-2 关于x=-1/2为中心的偶对称序列

令x′=x+1/2，于是f_s（x′）是以x′=0为中心的偶对称函数，其傅里叶变换为

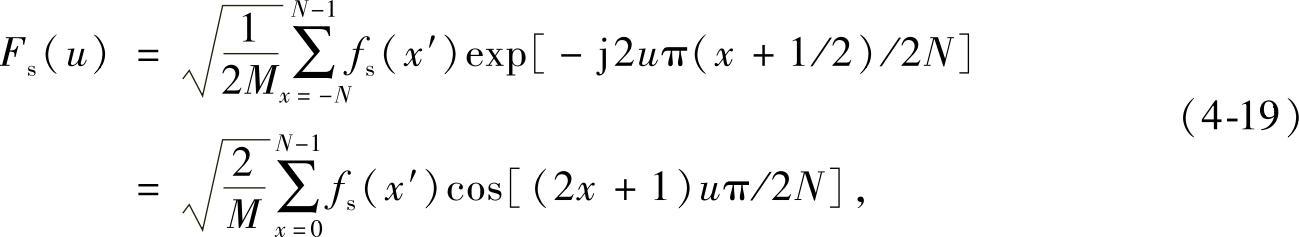
所以f_s（0）=0

根据式（4-18）知f_s（x′）和f（x）的关系如下：

f_s（-x+1/2）=f（-x）=f（x-1）=f_s（x-1/2），x∈[0，N] （4-20）

结合式（4-19）和式（4-20）可得f_s（x′）的傅里叶变换为

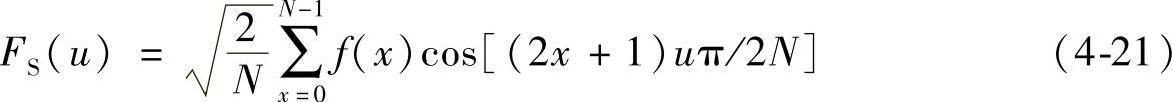
由式（4-21）确定的变换称为离散余弦变换（DCT）。对于长度为N的一维信号X，余弦变换定义T_C为

T_C=C_N·X （4-22）

正弦正交基元素由下列函数生成：

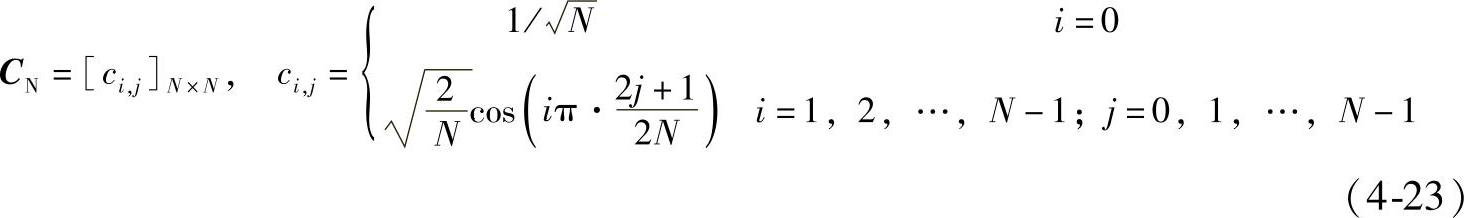
8阶正弦变换基函数如图4-3所示。

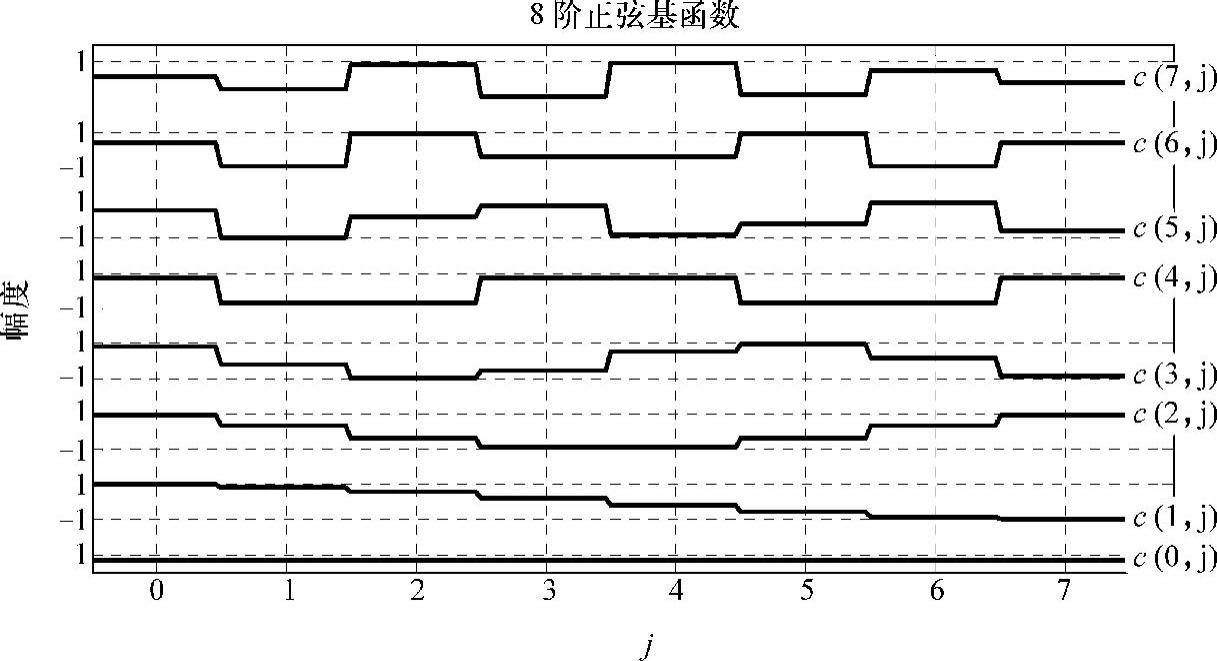
图4-38 阶正弦变换基函数

实现上述结果的MATLAB代码如下（省略画图部分）：

对于N阶正弦变换基C_N满足：

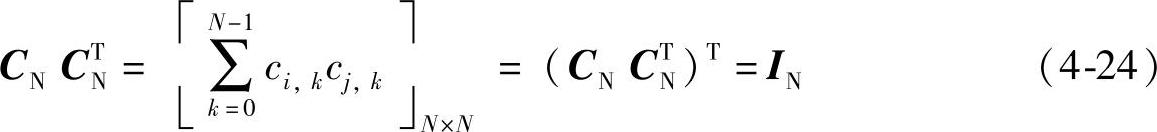
式中，I是N阶单位矩阵。证明如下：

证明：若i=j=0，显然有：

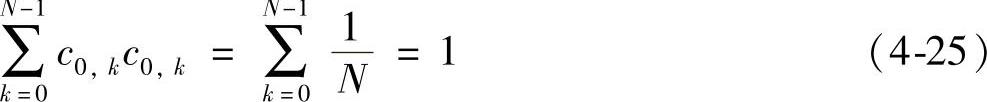
一般情况下，结合（4-23）得：

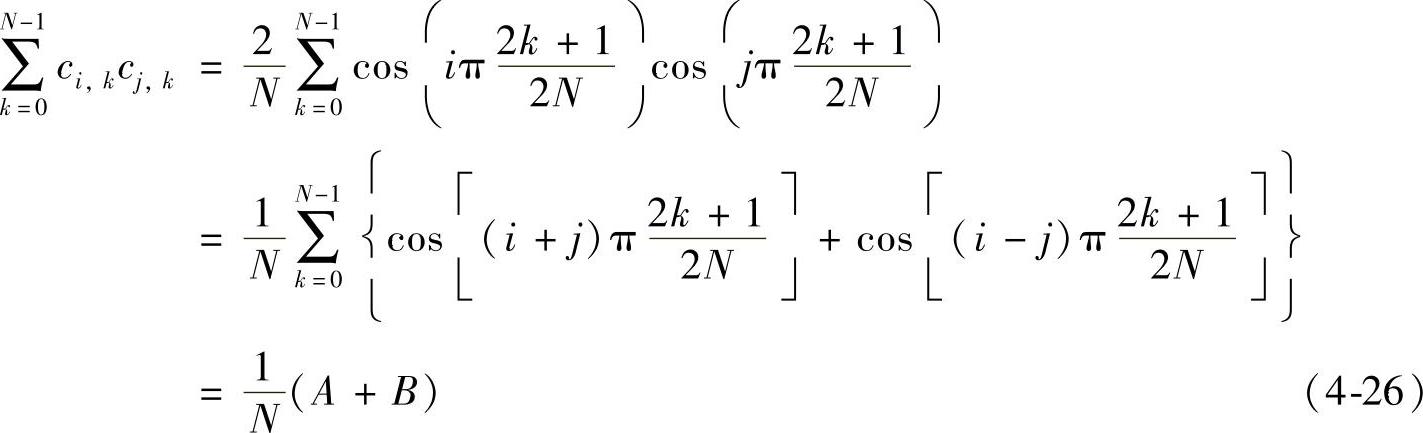
当i≠j≠0时，令n=（i+j）/2N，显然有0<n<1。式（4-26）中元素A为

同理可证，B=0；当i=j≠0时，同法可知A等于0，但显然B=N；当i=0或j=0时，结论同i≠j≠0情形。综合以上，可知：

结合式（4-22）和式（4-24），可知余弦反变换为

X=C^T_N·T_C （4-29）

需要指出的是，由于余弦变换基元素均为小数，在运算上较复杂。可通过近似为整数后变换，称为整数DCT，在H.264及AVS标准中被使用。对于4阶DCT，余弦变换基等于：

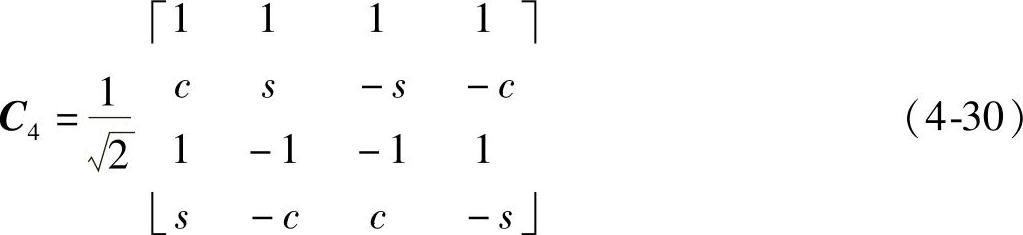
式（4-30）中，c=2cos（π/8）和s=sin（π/8）。近似取整的方式可以通过基乘上α后作某种规则的取整，也可通过按式（4-29）进行部分运算后步骤取整。不论采用哪种方式都会引入误差，如何分析误差分布规律及有效降低误差是值得研究的问题。余弦变换主要应用在数据内插、图像压缩方面，在MPEG-2、H.264、AVS等音视频压缩标准中得到了广泛应用。