首页理论教育了解沃尔什正交基

了解沃尔什正交基

2023-06-23 理论教育版权反馈

【摘要】：图4-14 阶沃尔什基函数对于N阶沃尔什变换基，定义在N点间隔内过零次数的一半定义为列率。由表4-1可看出，按列率排列的沃尔什基序号k是过零次数，故对应列率k/2；反之，沃尔什基的沃尔什变换是仅在列率为k/2时非零的N向量。性质1：两个不同列率的沃尔什基形成完备正交系，即基相乘产生列率搬移。表4-2 N=8列率搬移性质2：信号并元移位s的沃尔什变换等于信号沃尔什变换与列率s和沃尔什基乘积。

对于长度为N的一维信号X，沃尔什变换定义T_W为

T_W=Wal_N·X （4-9）

沃尔什正交基元素由下列沃尔什函数生成：

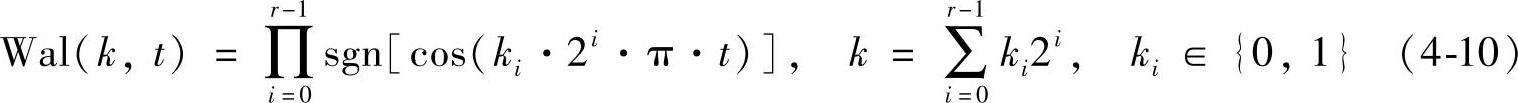
式中，sgn（·）是符号函数，即对于正数为+1，对于负数为-1；k_i是k用二进制表示的第i位数字；t为0到N-1归一化表示，即m/N（m=0，1，…，N-1）。例如对于N=4，r=2，k=0～3二进制表示k₀k₁分别为00/01/10/11时，沃尔什基底函数组成见表4-1。

表4-1 N=4的沃尔什函数

MATLAB实现沃尔什函数的代码如下：

运行结果如图4-1所示。

图4-14 阶沃尔什基函数

对于N阶沃尔什变换基，定义在N点间隔内过零次数的一半定义为列率（sequency）。由表4-1可看出，按列率排列的沃尔什基序号k是过零次数，故对应列率k/2；反之，沃尔什基的沃尔什变换是仅在列率为k/2时非零的N向量。对于沃尔什变换具有以下重要性质。

性质1：两个不同列率的沃尔什基形成完备正交系，即基相乘产生列率搬移。

证明：不同频率f_m和f_n的正弦函数相乘会出现f_m±f_n频率分量，即频率会发生搬移。对于列率分别为m和n的沃尔什基相乘过程如下：

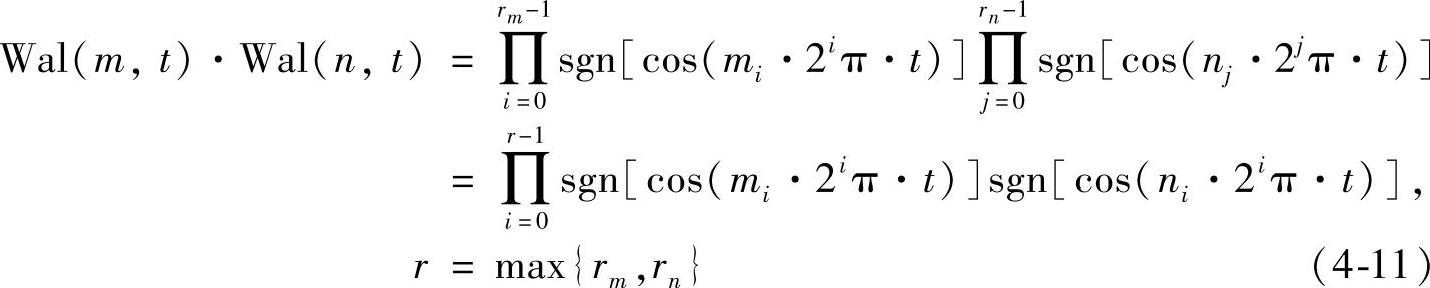
对于m_i，n_i∈{0，1}，区分相等和不等两种情况分析易知式（4-11）等于：

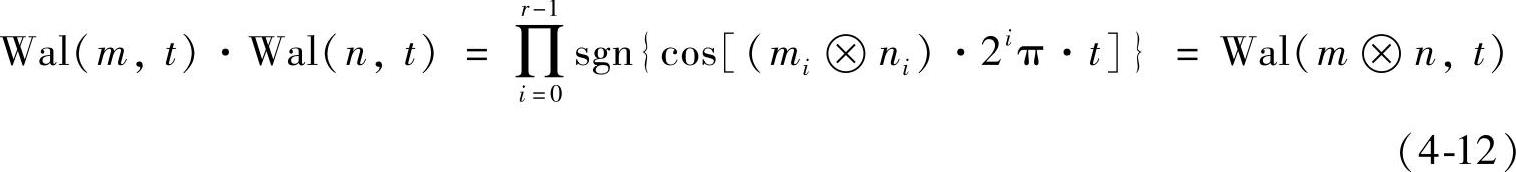
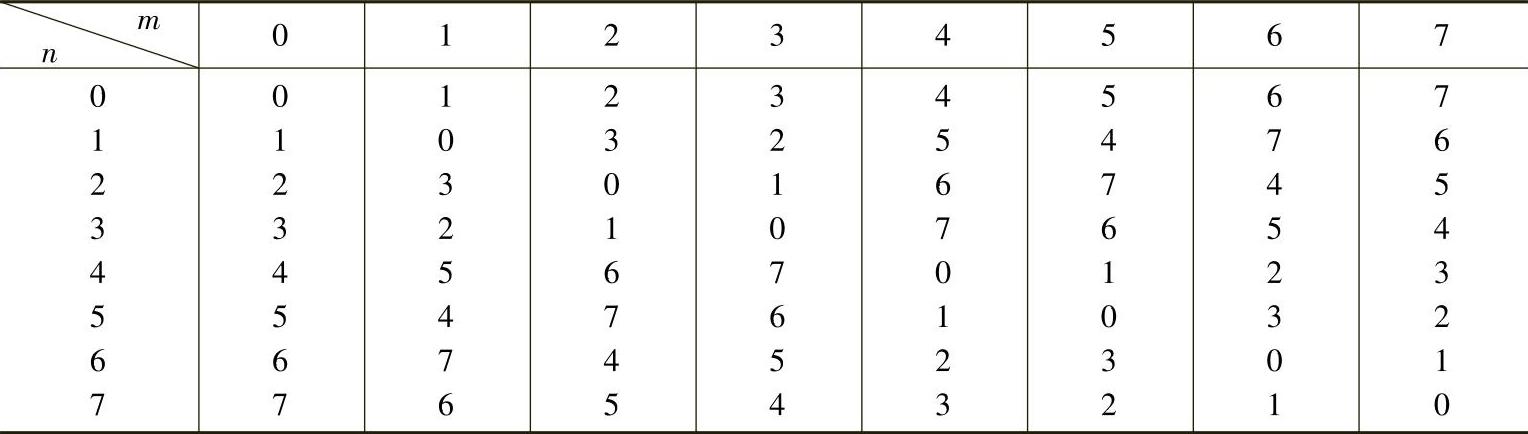
式（4-12）说明两沃尔什基函数相乘得到列率搬移的沃尔什基且其列率等于原两列率的模2异或。表4-2列出N=8时的搬移规律。

表4-2 N=8列率搬移

性质2：信号并元移位s的沃尔什变换等于信号沃尔什变换与列率s和沃尔什基乘积。

证明：对于沃尔什基坐标k和t（整数）取值线形无关均为[0，N-1]，所以由式（4-10）定义的沃尔什基矩阵具有对称性，即

Wal（k，t）=Wal（t，k）（4-13）

记信号[f（x）]=[f（0），f（1），f（2），f（3）]，定义[f（xs）]为列率并元移位s位后的序列，用[f（x）s]来表示。显然，xs的意义为信号[f（x）]中各元素序号与s异或得到的重排序即列率搬移。设[f（x）]和[f（x）s]的沃尔什变换分别为[F（k）]和[F（k）s]，即

如[f（x）]=[1，2，-1，3]，则[F（k）]=[5，1，3，-5]/4；[f（x）2]=[-1，3，1，2]，求得对应的沃尔什变换[F（k）2]=[5，-1，-3，-5]/4=[F（k）]·Wal（k，2），证明了结论的正确性。

性质3：信号循环并元卷积的沃尔什变换等于信号沃尔什变换的乘积。

证明：信号f（x）g（x）的循环并元卷积定义如下：

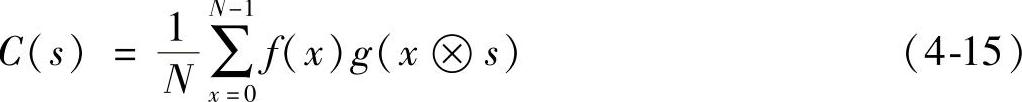
C（s）的沃尔什变换如下：

沃尔什反变换如下：

沃尔什变换主要应用在图像压缩、语音处理、滤波和功率谱分析方面。