首页理论教育基于矩形二叉分解的基窗优化设计

基于矩形二叉分解的基窗优化设计

2023-06-23 理论教育版权反馈

【摘要】：基于此提出了“基于矩形窗二叉分解的基窗设计”算法，对各级分解得到的基窗使apDW特性在性能A和B之间有了较大的灵活选择性。这样，F可由若干级二叉分解基窗卷积生成，即式中，Rjni表示第j级第i个二叉分解右分支中长度等于ni的窗函数，最终可分解成若干个长度为2的矩形窗卷积，只进行1级分解的结果F就是三角窗。

设计FIR滤波器时，带宽和阻带最小衰减相互矛盾，窗函数通过在频域与理想滤波器卷积会增大带宽，但可获得较大的最小旁瓣衰减。由3.1节介绍的窗函数作用可知，理想窗谱应是一个冲击函数，这样卷积得到的仍是理想滤波器。但冲击谱对应的是无限长时域信号（即不对信号进行截短），这显然不切实际的。高主-旁瓣幅值比和窄主瓣宽度是设计优良窗的两个焦点。基于此提出了“基于矩形窗二叉分解的基窗设计”算法，对各级分解得到的基窗使apDW特性在性能A和B之间有了较大的灵活选择性。

由式（2-46）并结合定理2可知，对于具有线性相位的apDW卷积窗C谱应等于前基窗F谱与其共轭的乘积，即

P_D（e ^jω）=P_F（e ^jω）·P_F*（e ^jω）=P_F（ω）2=P_D（ω）（3-22）

式（3-22）说明窗C谱是恒为正的实函数且幅值等于基窗F谱值的平方。16阶三角基窗F和卷积窗C谱形状及主瓣占比如图3-25所示。

由图3-25可以看出，卷积窗C谱幅频特性改善明显。这是因为基窗F谱自乘时，主瓣和旁瓣幅值低于1的部分都按照二次方算子减弱了，且相对幅值越小减弱幅度越大。其次，共轭谱幅频特性相同使卷积窗C主瓣宽度和零点个数保持不变。显然，这种谱相乘次数越多，结果就越接近冲击谱。但对于长度为偶数阶N的数字三角窗是由N/2阶和N/2+1阶两个矩形窗卷积生成，则卷积窗C谱的零点会增加N/2+1个而过渡带宽度则会降低2/（N+2）。以Bartlett为基窗apDW的卷积窗C_d及其谱Pd与基窗F之间关系如图3-26所示。

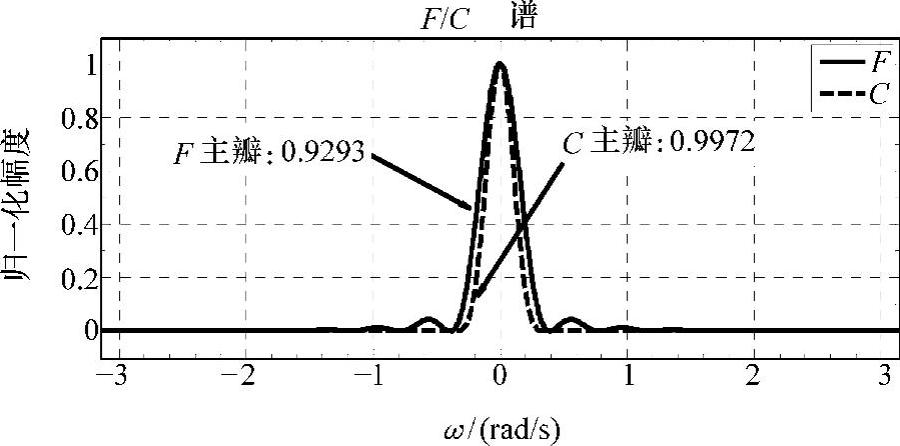
图3-25 32阶基窗F和卷积窗C谱特性

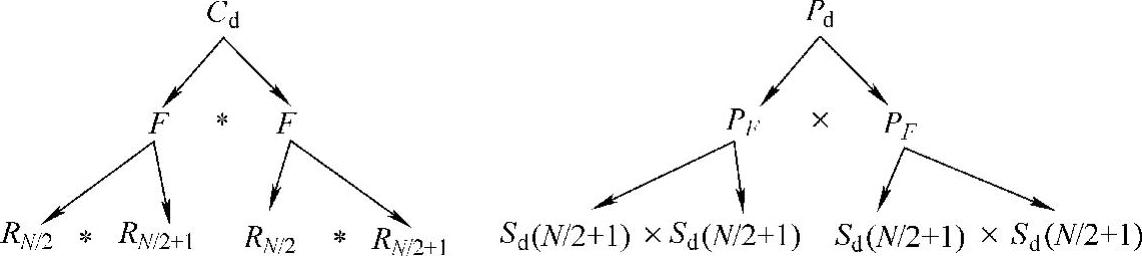
图3-26 卷积窗C和基窗F谱对应关系

由图3-26可看出，C_d谱是若干个矩形窗谱乘积，其主瓣宽度应由最小阶窗决定，因此为保持过渡带最低程度放大，每级都应以准等长矩形窗进行分解。将上面过程进一步深化，认为“矩形窗”只是分解过程的中间结果，即它是由低阶矩形窗卷积产生（结果不再是矩形窗）。这样，F可由若干级二叉分解基窗卷积生成，即

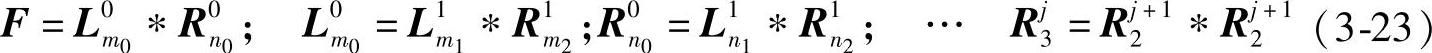
式中，R^j_ni表示第j级第i个二叉分解右分支中长度等于n_i的窗函数，最终可分解成若干个长度为2的矩形窗卷积，只进行1级分解的结果F就是三角窗。式（3-23）可用图3-27来加以说明。

尽管每级分解得到的两子窗长度有多种组合，但为保证卷积窗C过渡带宽度最小，应采用准等分方式进行，如N=8时的完全分解如图3-28所示。

显然，第k级父窗与第k+1级子窗长度有下面关系：

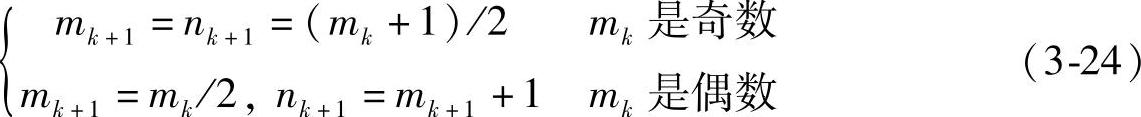
假设上面二叉树中有n个叶片，根结点F就是n个叶片R₂的卷积，所以有

N=2n-n+1⇒n=N-1 （3-25）

则完全分解得到的卷积窗C谱等于

因为R₂的过渡带宽度是π，所以由式（3-26）完全分解得到的卷积窗C过渡带很宽，不彻底分解可缓解这一问题。假设apDW阶数N=2^M，则二叉分解的最大级数为M。在第m级中（1≤m≤M-1）共有2^m个矩形，其中最短一个矩形长度为2^M-m，其余2^m–1个长度为2^M-m+1，则对应的卷积窗C谱为

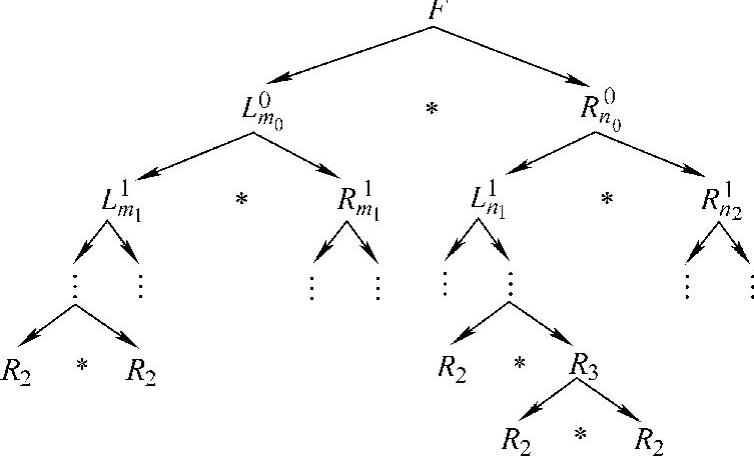
图3-27 基于矩形窗二叉分解

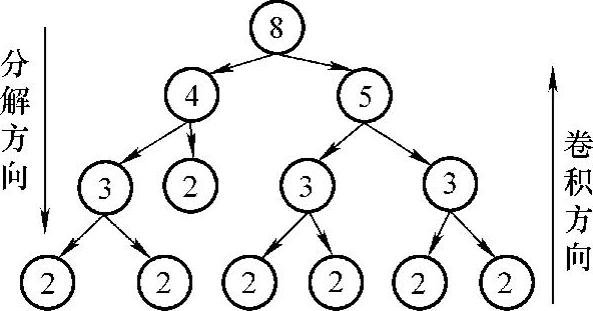
图3-28 8阶卷积窗C的完全分解模式

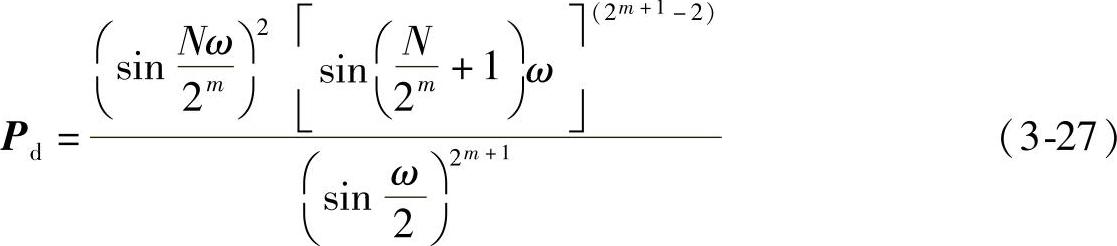
由其中最小长度矩形决定的过渡带宽度为

因此，分解级数每增加一层，相应的F过渡带宽就增加一倍。如利用二叉等分分解设计N=32截止频率为π/2的apDW，完全分解得到各级基窗及特性如图3-29所示。

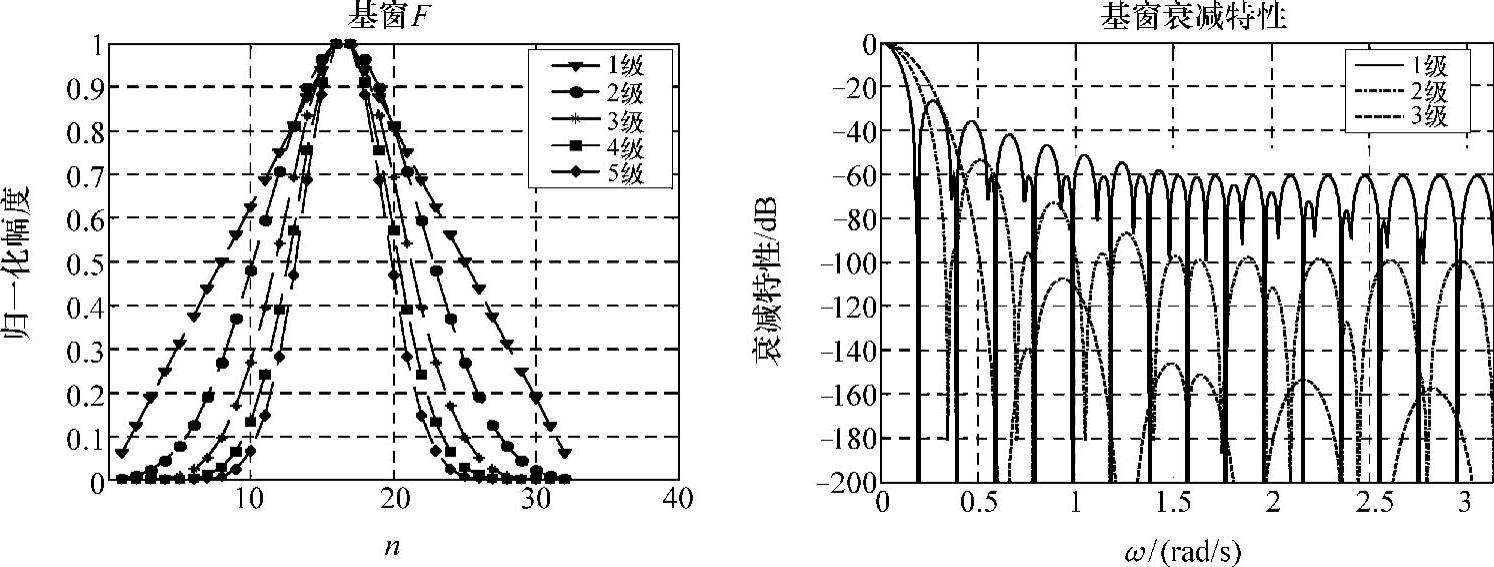
图3-29 5级分解基窗F及特性

由窗谱衰减特性可看出，随着分解层数增加，最大旁瓣峰值急速下降，第4级别达到-209.56dB，第5级则为-358.14dB。各级别基窗F特性见表3-3。

表3-3 各级别基窗F指标

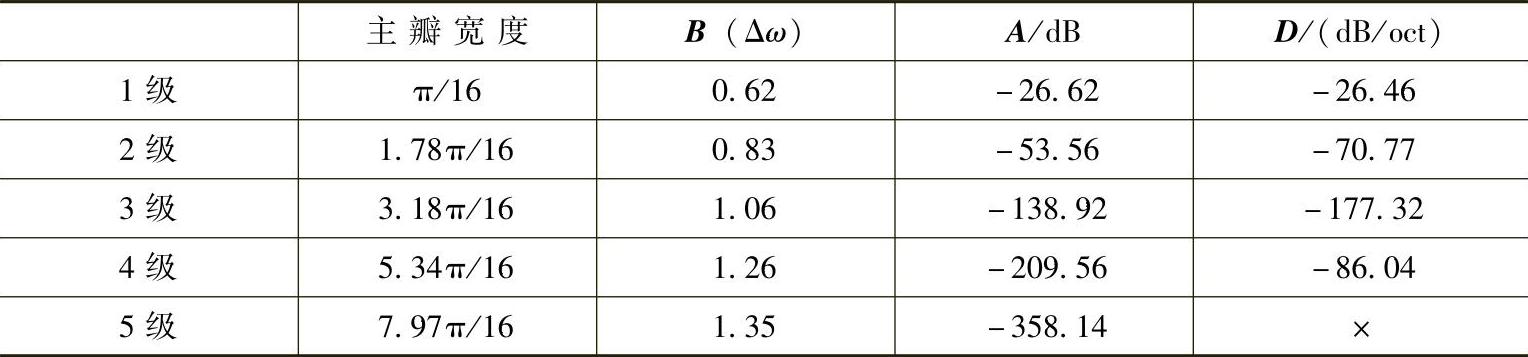
第5级基窗F没有旁瓣，所以无法给出它的第一旁瓣衰减A和倍频衰减D。比较表3-2与表3-3可以看出，二叉分解得到的基窗具有很大的波峰衰减率和较窄-3dB带宽，是新类型窗函数，其缺点是高级分解时过渡带较宽，但通过加大N可缓解。

以各基窗F建立的滤波器特性如图3-30所示。

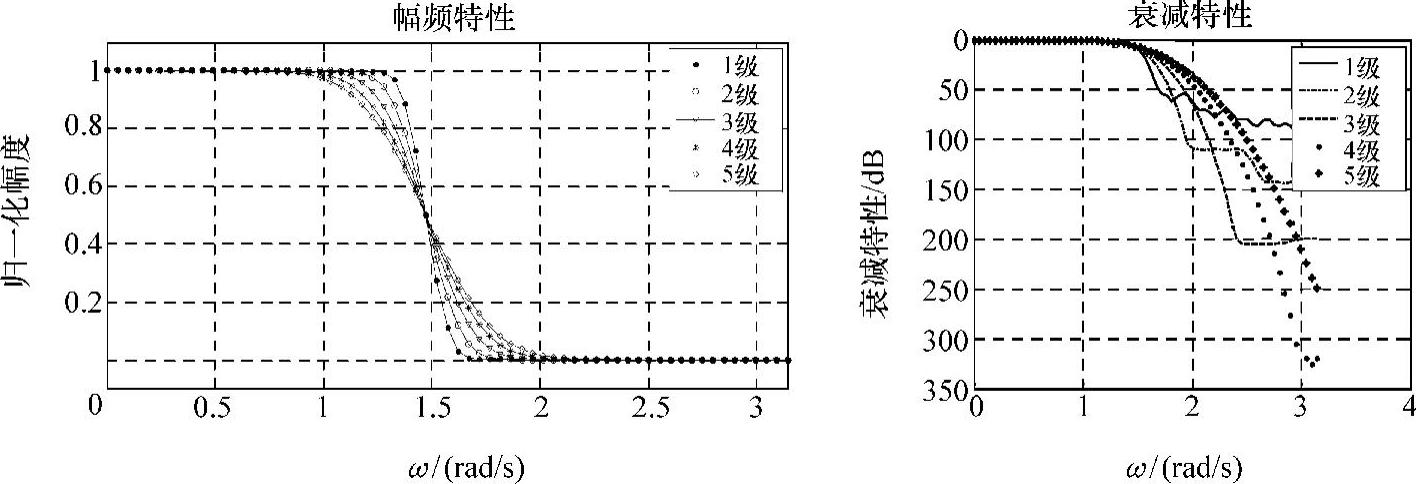
图3-30 基于各级基窗F的apDW特性

由实验结果可以看出，基于二叉分解法得到基窗的apDW具有十分理想的衰减特性。等分二叉分解层次越高，衰减特性越好，但过渡带较宽。图3-30中，第3级分解曲线旁瓣波纹十分理想。实现上述结果的MATLAB代码如下（只列出二叉分解函数biTree，滤波器特性曲线genapDW及画图函数todraw省略）：