【摘要】:为寻找更为理想的基窗函数,借助LMS算法思想提出了“基于LMS准则以apSW为模型的基窗函数设计方法”。图3-21 余弦基神经自适应网络图3-21 余弦基神经自适应网络图3-22 apSW基窗LMS设计算法按照流程图,设计截止频率为π/4的32阶低通apSW的窗函数F。
3.1节在对6种基窗函数分析的基础上,指出以余弦窗为基窗的apDW具有最小的频率采样误差。这种比较是有局限性的,首先比较是在固定基窗模式下进行,对于其他未知形状的窗并没有进行推论或衡量。此外,在对比时,对于频带中其他频率成分的误差并不能同时保证为最小或提出充分条件。为寻找更为理想的基窗函数,借助LMS算法思想提出了“基于LMS准则以apSW为模型的基窗函数设计方法”。即将[0,π]间的频率采样点ωi的取值定义为随机过程,通过最小频采误差为收敛准则构造收敛模型,设定apSW具有线性相位且N为偶数(N为奇数时可作类似分析)。
式(2-51)表示的幅频特性可表示成如下表达式:
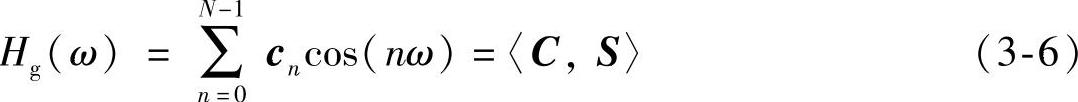
式中,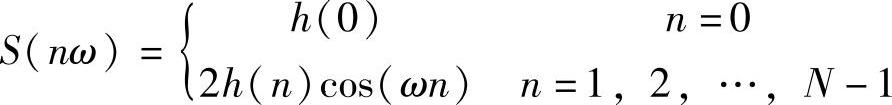 。把式(2-57)结论表达式cn代入上式并由基窗f的中心对称性得:
。把式(2-57)结论表达式cn代入上式并由基窗f的中心对称性得:
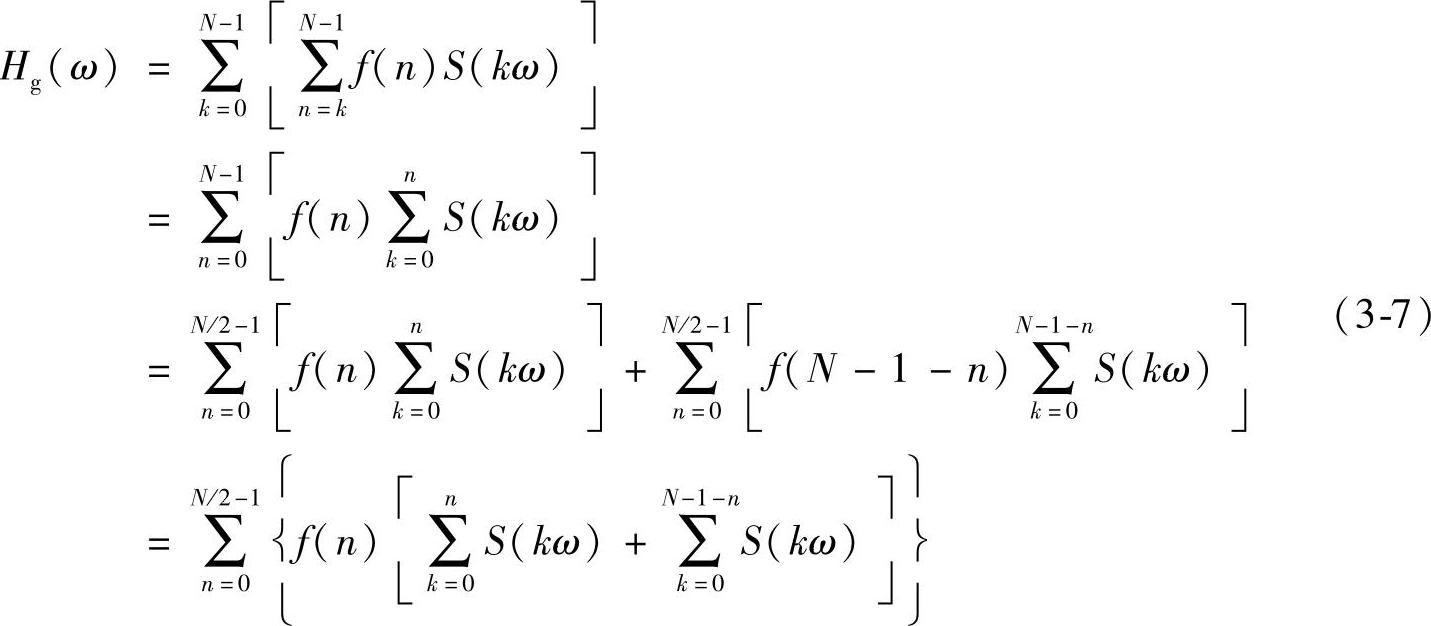
式(3-7)表明,对于N阶线性相位apSW,只需f半边信息就可得到幅频特性。重新定义基窗向量F如下:
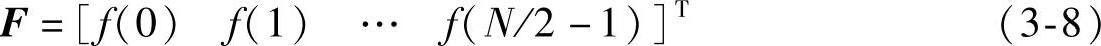
并定义余弦向量为
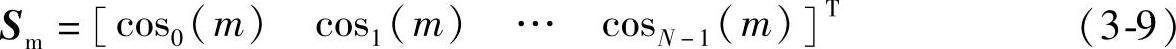
式中,cosn(m)=cos(nωm)n=0,1,…,N-1;m=0,1,…,M,M是实验样本数。构造冲击响应加权矩阵G如下:
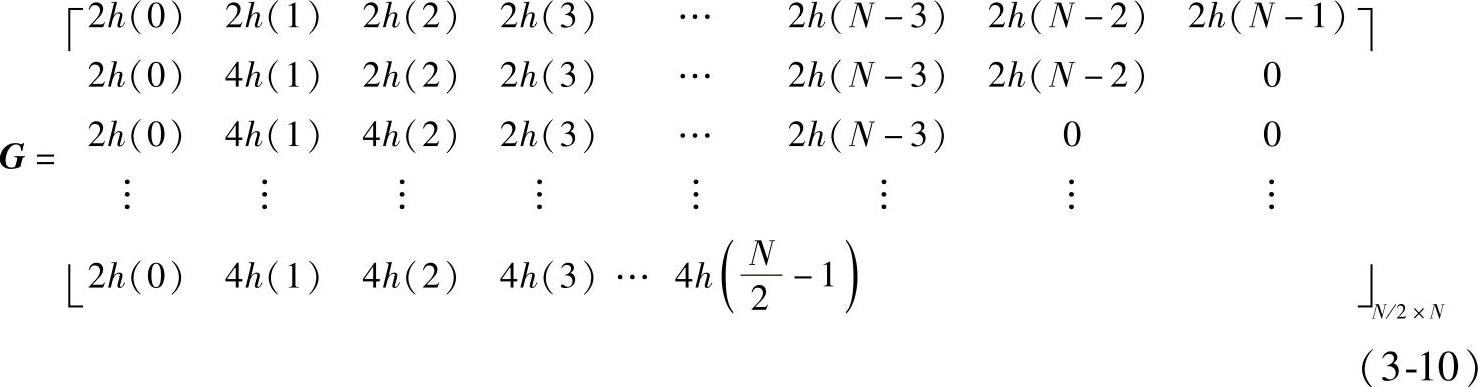
幅频响应矢量Hg为
Hg=[Hg(ω0)Hg(ω1)…Hg(ωM-1)]T (3-11)
结合式(3-8)~式(3-11)重写式(3-7)如下:
Hg(ωm)=FT·G·S m=0,1,…,M-1 (3-12)
设apSW理想幅频响应矢量为Hi。当样本点数为M时,Hi可表示如下:
Hi=[Hi(ω0)Hi(ω1)…Hi(ωM-1)]T (3-13)
则apSW的实际幅频响应Hg在ωm处的误差εm为
εm=Hi(ωm)-Hg(ωm)=Hi(ωm)-FT·G·S (3-14)
在区间[0,π]内选取ωm方式任意,故可将ωm看作是区间[0,π]内的随机变量,则它的函数Hi和G满足平稳随机分布。误差εm也具有随机性,故可用均方误差ξm=E{εm2}作为判定准则,使其达到最小值对应的基窗向量F即在此准则下的优化基窗函数,F可采用最陡下降法进行求解。根据式(3-14)可得到均方误差为
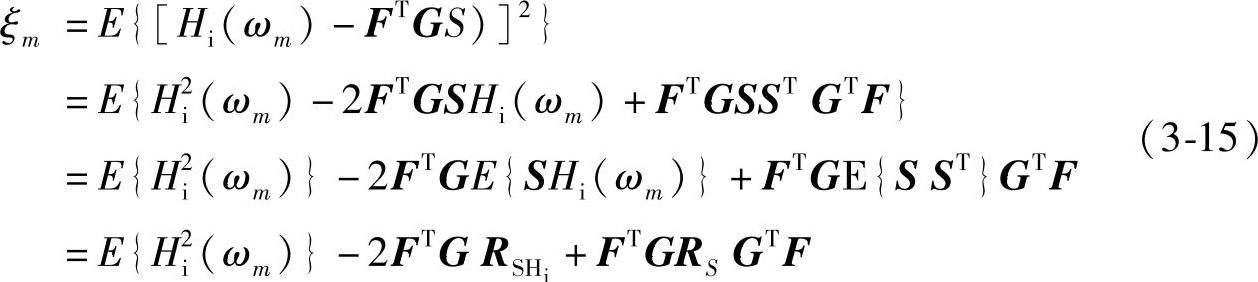
式(3-15)中RSHi和RS分别是Sm与Hi互相关和Sm自相关矩阵,即
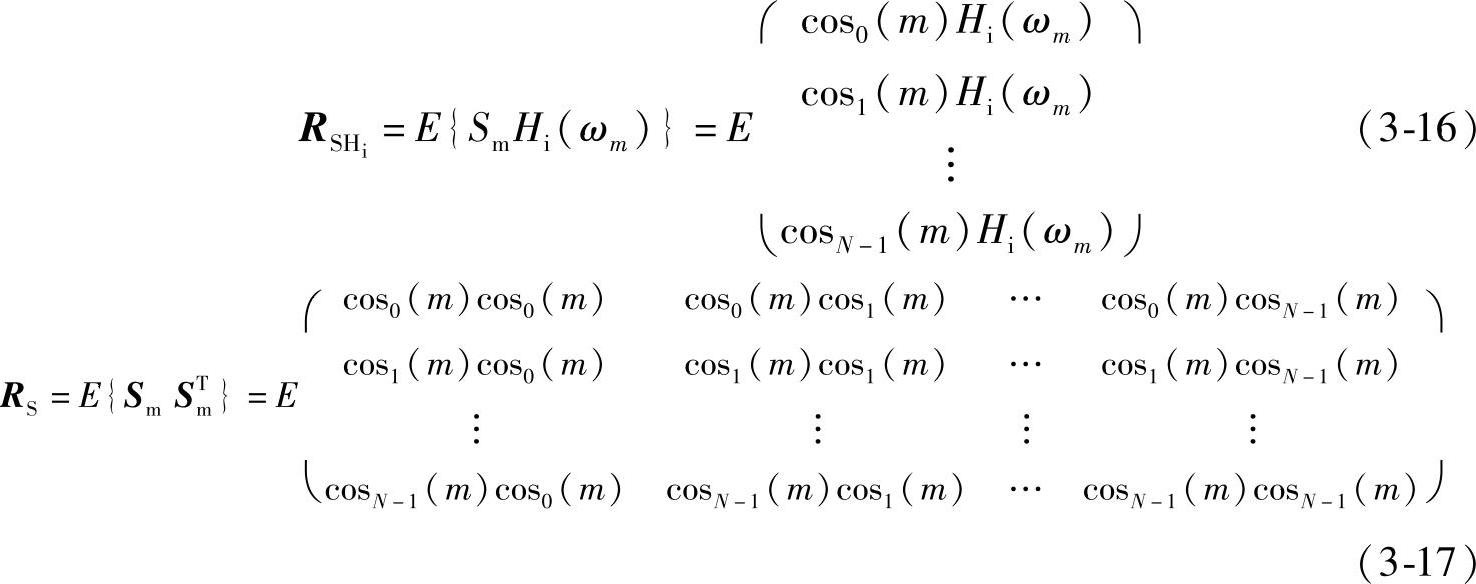
对式(3-15)运用最陡下降法得到递推公式为(https://www.chuimin.cn)
Fm+1=Fm+μεmG·Sm (3-18)
式中,Fm表示第m次迭代得到的窗函数。为保证均方误差收敛,步长μ应满足0<μ<λmax,λmax是GRSGT的最大特征值,可证明其满足:

式中,hi是向量h的第i个元素。N阶apSW实验样本数M可由下式确定:
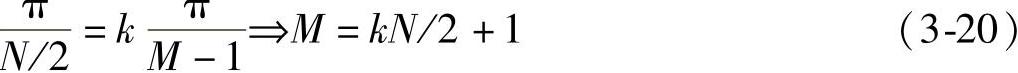
式(3-20)中k是大于1的整数。这样保证在每两个频采之间有k-1个实验样本,若控制这些点使其幅值逼近理想值,就可使均方误差收敛到误差限εmax以下。对于阶跃点之间的样本插值,在不增加过渡点的前提下,将其归为阻带或通带范围均可。由M确定的实验频率为
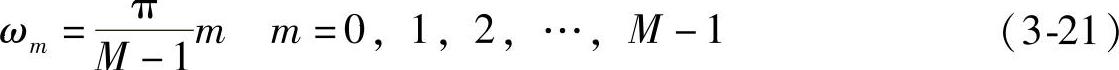
这样,以式(3-19)定义步长并按照式(3-18)进行迭代,直到基窗F使ξm≤εmax成立即可。以上过程可用图3-21构造。相应的算法流程如图3-22所示。
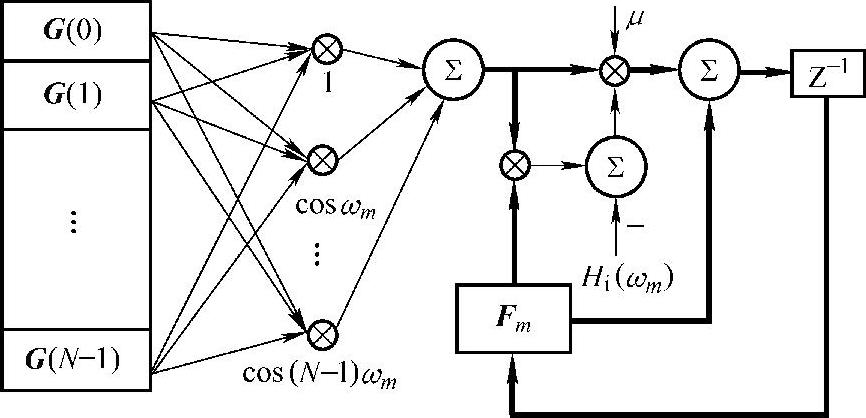
图3-21 余弦基神经自适应网络
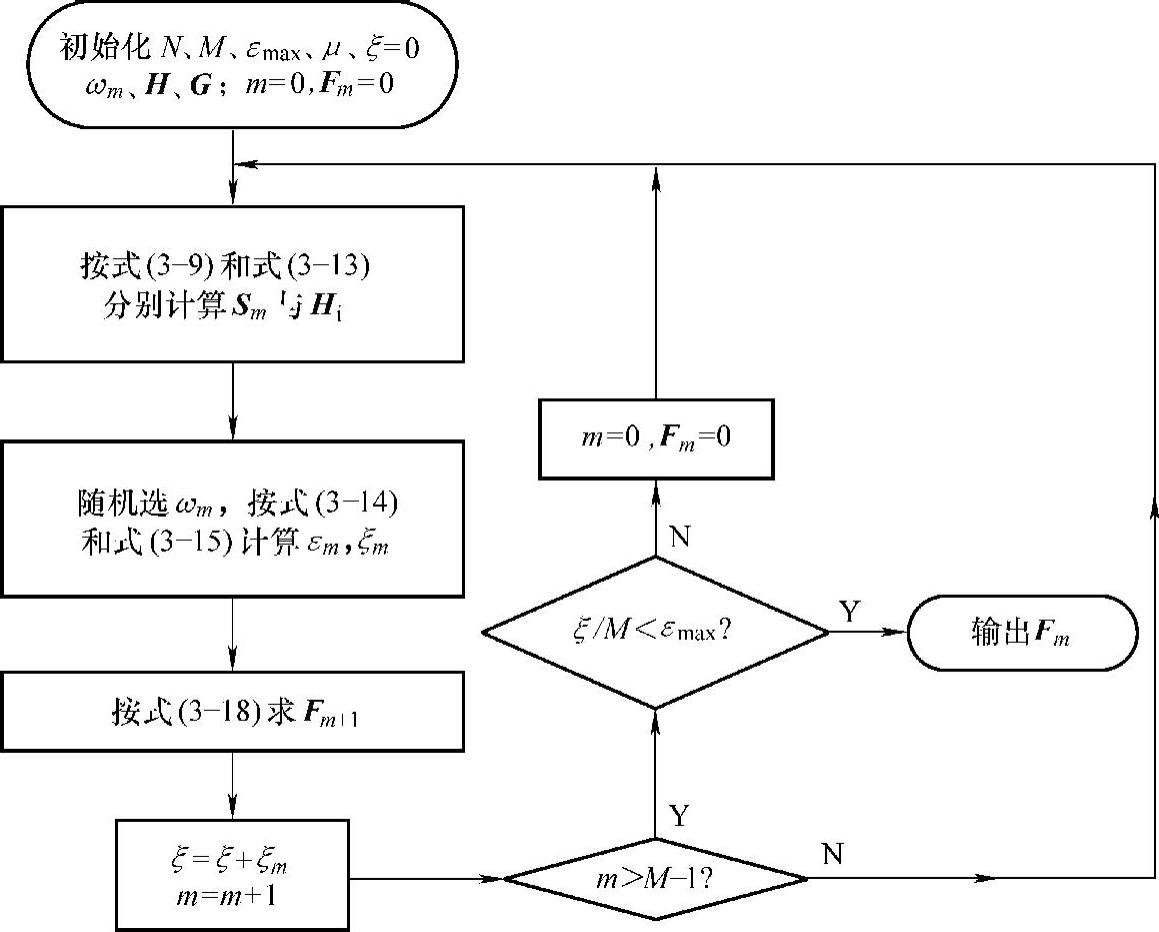
图3-22 apSW基窗LMS设计算法
按照流程图,设计截止频率为π/4的32阶低通apSW的窗函数F。取H=[1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1],半带中频采点数为(32-2)/2+2=17。在式(3-20)中令k=2,样本点均匀地在频采点之间抽取,得到样本容量M=33,则实验频率ωm=mπ/32(m=0,1,…,31)并令εmax=0.001。以随机方式选取样本进行迭代,步长μ=0.3951,修正后等于0.2371,初始基窗F0=0。具体的MATLAB代码如下(省略画图部分):

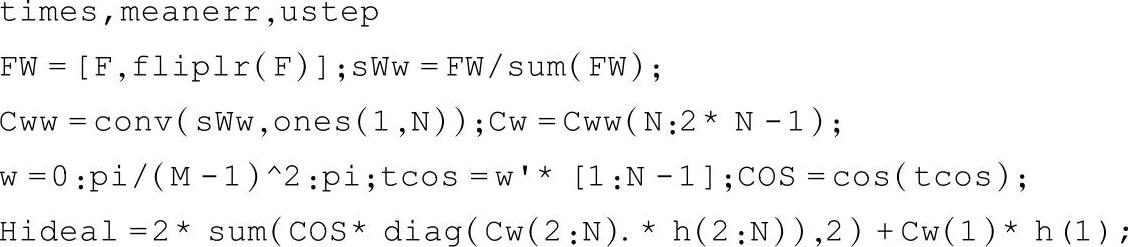
在CPU主频为2.6GHz的计算机上运行共迭代26462次,耗时22.267324s,得到apSW与理想幅频响应的均方误差为6.5692×10-4。收敛得到的基窗(归一化后)F=[0.0050 0.0046 0.0189 0.0229 0.0205 0.0255 0.0325 0.0327 0.0371 0.0401 0.0402 0.0409 0.0447 0.0448 0.0441 0.0455]。滤波器幅频响应、衰减特性和基窗F及对应的卷积窗C如图3-23所示。
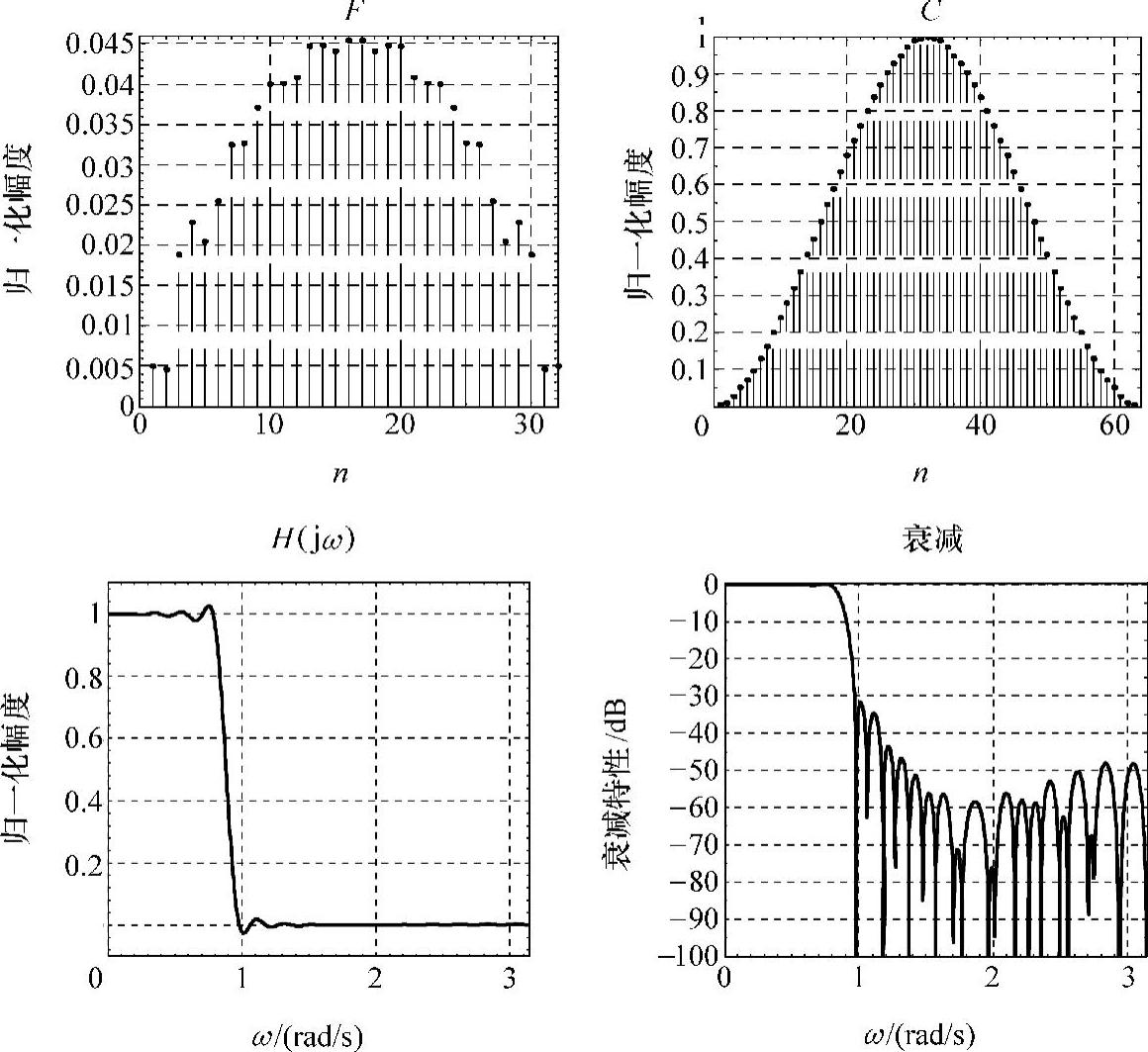
图3-23 实验得到的基窗及apSW特性
由图3-23可看出,第一旁瓣最小衰减降至-32.5dB,过渡带宽度约为4.55π/63。将此参数对比表3-1各窗特性可知,通过此自适应算法得到的基窗在B和A两方面同时得到改善,窗口加速度sw等于143,大于现有的7种基窗。通带和阻带内的振荡幅度都得到较大程度抑制,但在过渡带附近出现了尖缝,这是由于实验中对处于阶跃点之间的一个样本只简单地将其归为通带而导致。这可以通过插入过渡点来得到改善,但过渡带也将加宽。基于基窗F的apDW特性如图3-24所示。
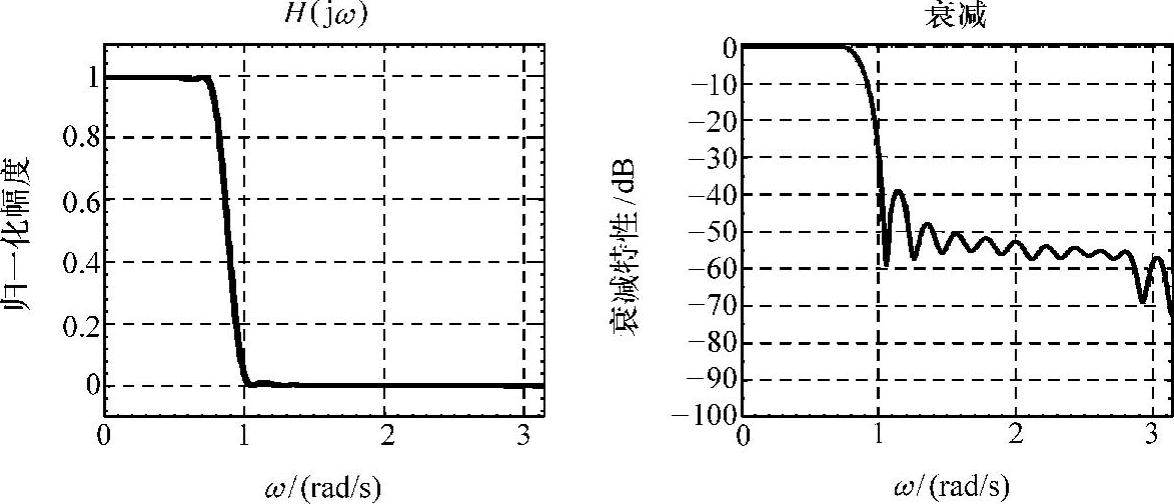
图3-24 基于F的apDW特性
比较图3-23和图3-24可以看出,apDW进一步降低了旁瓣最小衰减至-38.9dB,过渡带宽度约为7π/63,窗口加速度sw等于111。此外,apDW波动比apSW少了很多,但阻带内没有-∞点,这是因为它不具有零点而致。
以上基于LMS准则基窗设计方法的一个前提条件是不增加过渡点,这样得到的窗具有较大的窗口加速度。若侧重改善指标A,则可通过增加不同幅度的过渡点来实现,而幅度的选取也可通过自适应方式实现。此外,算法对ωm的随机选取而得到不同精度下的基窗,如何设置基窗初值和收敛步长是平衡精度和速度关键。

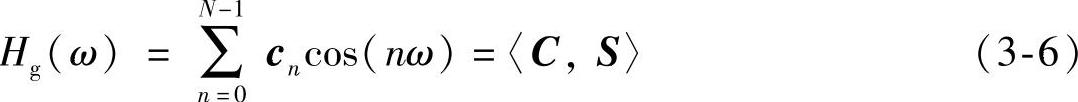
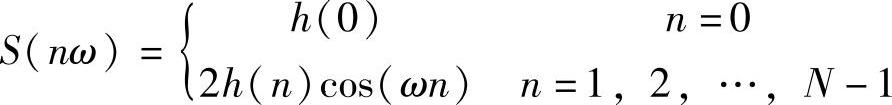 。把式(2-57)结论表达式
。把式(2-57)结论表达式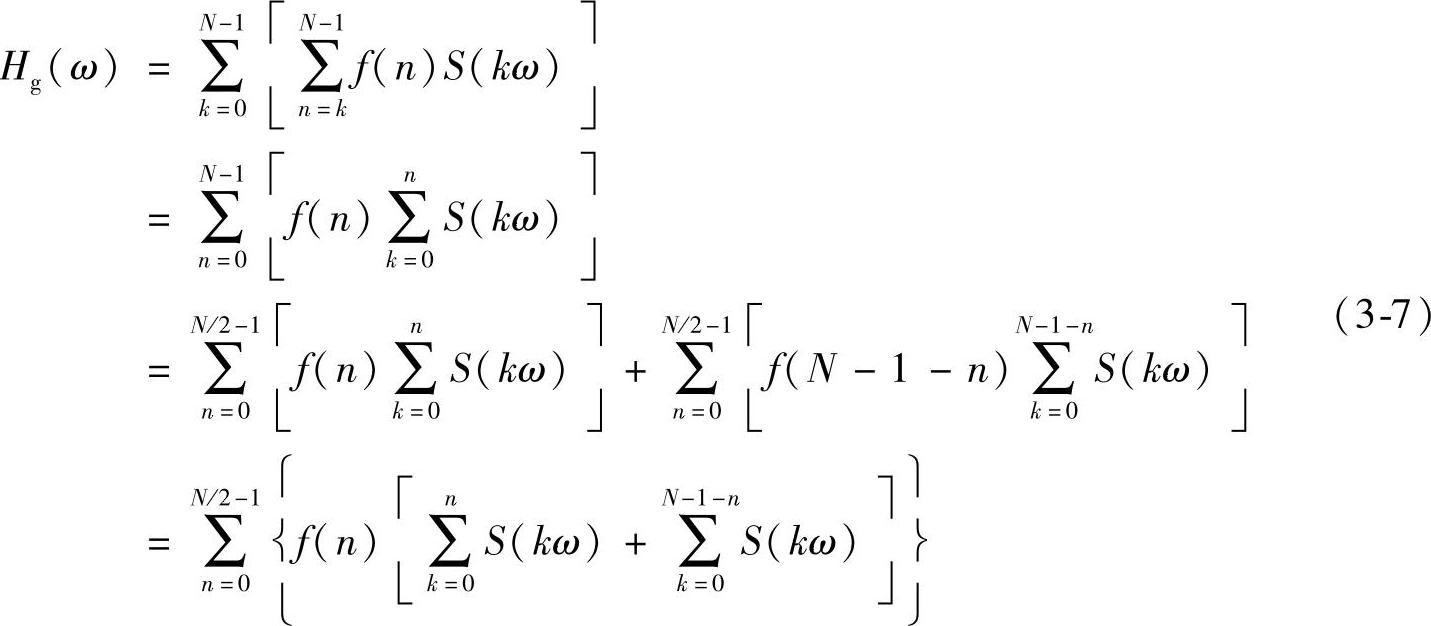
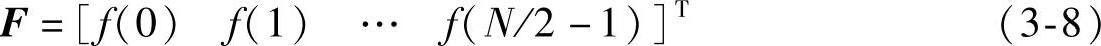
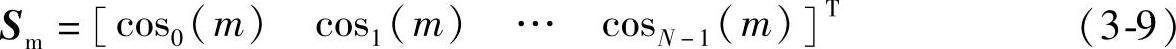
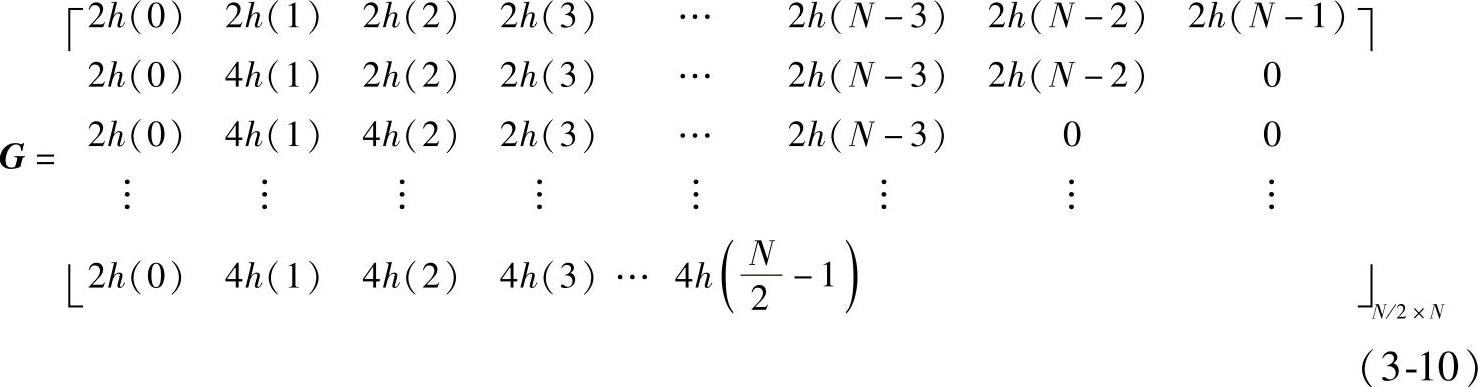
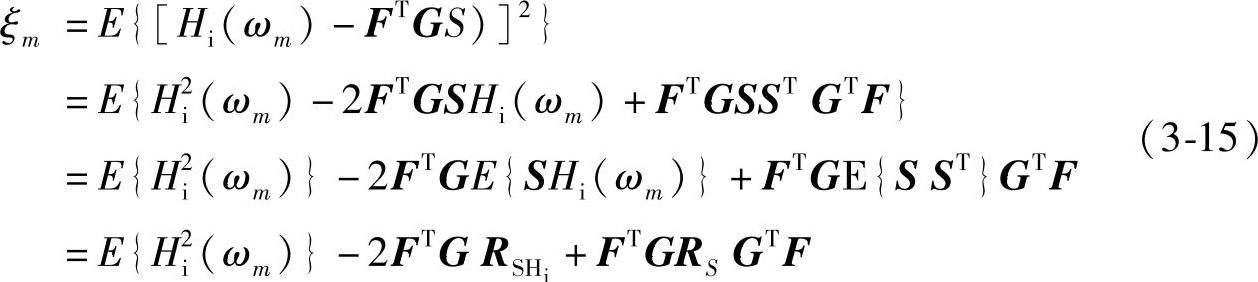
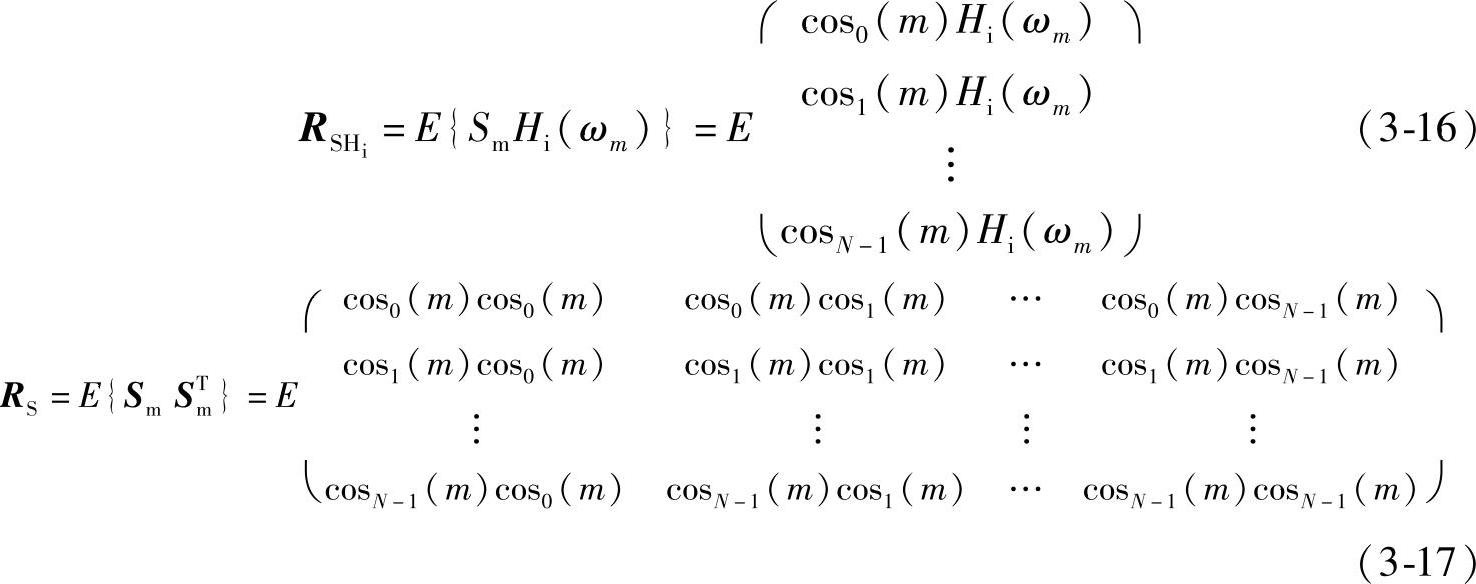

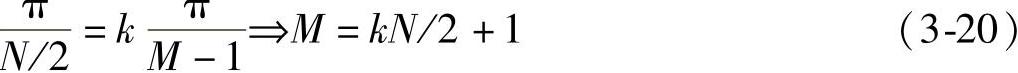
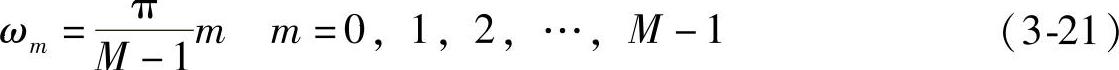



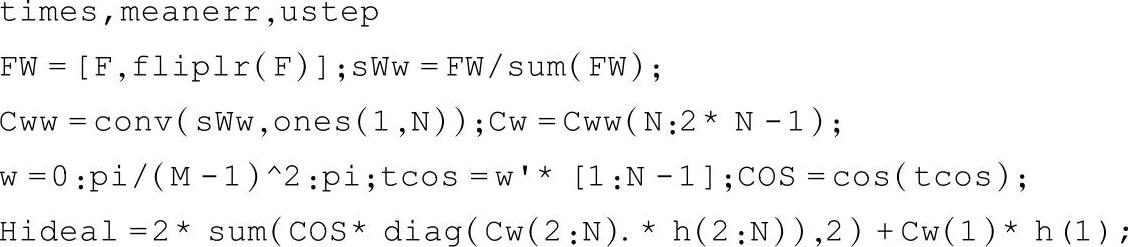








相关推荐