分析apDW频率取样误差

2023-06-23 理论教育版权反馈

【摘要】：图3-19 六基窗apDW频率采样误差分布六基窗apDW频率采样与理想频率采样之间的误差见表3-2。截止频率为π/2的apDW，频率采样误差随N变化的曲线如图3-20所示。图3-20 六基窗apDW频率采样误差随阶数变化曲线基窗为三角窗时的频率采样误差出现“奇偶振荡”现象，且随N增大而增大并趋于平稳收敛于0.2501。

由第2章中内容可知，apNW和apSW的频偏向量E_n元素恒为N，其传输特性在频率采样点与H对应取样相同。但apDW的E_n值并不恒定，其浮动程度反映了传输特性在各频率抽样点与H的偏差。以上节介绍的六种窗（矩形窗除外）分别作为apDW的基窗时（归一化）E_n曲线如图3-17所示。

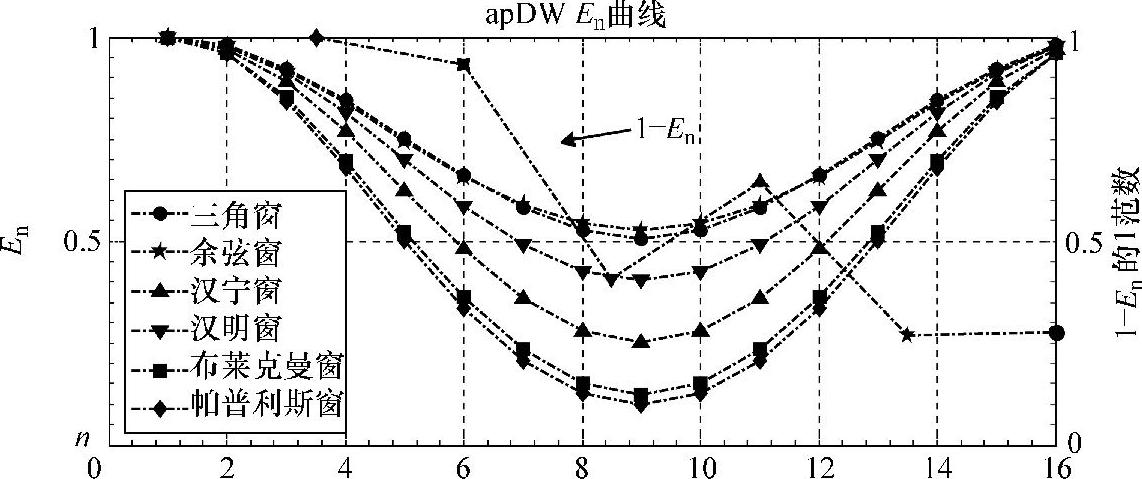
图3-17 apDW六种基窗的En

由图3-17可看出，六种基窗频偏均具有“盆”形状，余弦窗频偏稍低于三角窗，两者频偏最小。实现上述结果的MATLAB代码如下：

余弦窗的E_n曲线凹陷幅度随N不同而稍有变化，且N相当大时“盆底”幅值收敛于0.64。余弦窗阶数N从8增大至64时的E_n曲线变化趋势如图3-18所示。

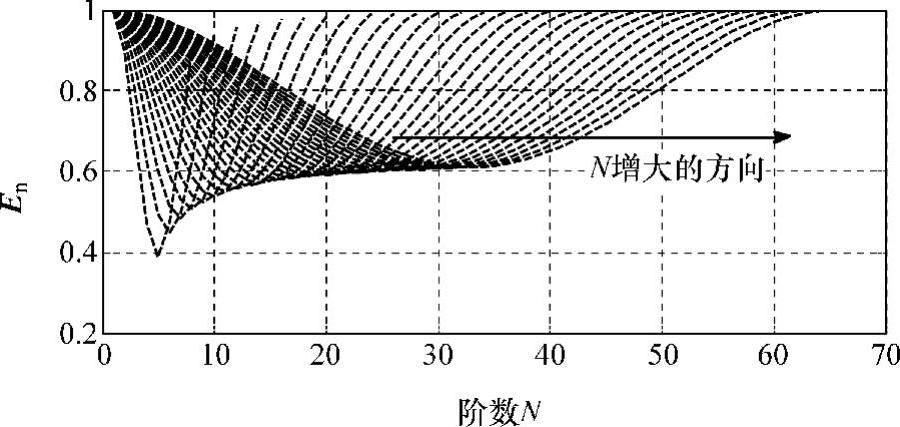
图3-18 余弦apDW系统E_n随阶数变化曲线

三角窗、汉宁窗、汉明窗、布莱克曼和帕普利斯窗的频偏向量E_n随N化规律与余弦窗类似，在阶数相当大时分别收敛于0.5、0.33、0.47、0.18和0.15，再次证明了余弦窗最小E_n的恒定性。实现上述结果的MATLAB代码如下：

以上说明了不同基窗形成的卷积窗C作用于系统H，对应的幅频特性的频偏误差也不同。例如N=32且截止频率为π/2的apDW低通滤波器，分别以上述6种窗为基窗，分析并比较在采样点处的误差大小。将半带滤波器分成通带、过渡带和阻带3部分进行观察，曲线如图3-19所示。

图3-19 六基窗apDW频率采样误差分布

六基窗apDW频率采样与理想频率采样之间的误差见表3-2。

表3-2 频率采样与理想频率采样之间的误差

由表3-2可以看出，余弦窗对应的特性与H距离最小，三角窗稍大，帕普利斯窗窗距离最大。余弦窗这种优势基本上都是在过渡点上获得，而在通带和阻带内频率采样误差都大于三角窗。实现上述功能的MATLAB代码如下：

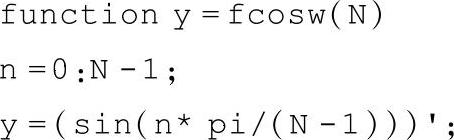
此外，频率采样误差也随阶数N的增大而增大。由生成图3-18结果的实验可知，当N相当大时的频率采样误差也将趋近于稳定。截止频率为π/2的apDW，频率采样误差随N变化的曲线如图3-20所示。

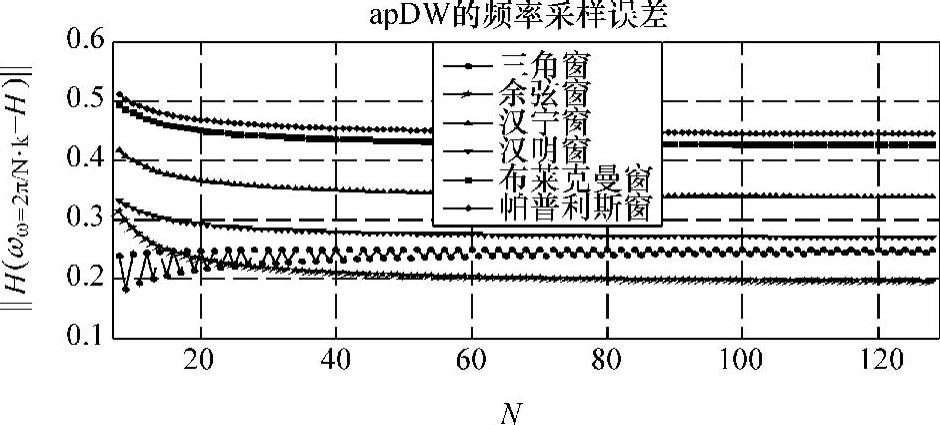
图3-20 六基窗apDW频率采样误差随阶数变化曲线

基窗为三角窗时的频率采样误差出现“奇偶振荡”现象，且随N增大而增大并趋于平稳收敛于0.2501。其他基窗对应的频率采样误差均满足递减规律，其中余弦窗具有最低误差和最大的下降速率且收敛于0.1912，其次是汉明窗收敛于0.2672，第三是汉宁窗收敛于0.3346，第四是布莱克曼窗收敛于0.4221，帕普利斯窗对应的频率采样误差最大，收敛于0.4413。由图3-20还可以看出，当阶数大于80后的误差水平趋于稳定，从而提供了选定阶数的一种限定基准。而且由图3-19可知频率采样距离分布不均匀，所以并不能通过任意增大N以达到理想特性。另外，频率采样距离的大小也会受通带或阻带宽度的影响（实现代码基本与freErrs相同，不再列出）。

分析apDW频率取样误差

相关推荐