从形式上看,带参数的宏调用和函数调用没有什么区别,而且确实在一些情况下它们产生同样的结果。例如:程序1:这两个程序的主函数main()是完全一样的,调用宏和调用函数得到相同的运行结果,都是5。理由是使用宏比函数调用更快。因为宏在真正编译之前已被相应地替换,在执行时,不必打断调用程序的运行,也没有参数的传递。......
2023-11-18
对窗向量w总的要求是希望其频谱中主瓣尽量窄,边瓣幅度尽量小,即频域能量主要集中在主瓣内。此外,w还应满足下列要求以便可定量地比较各窗性能:
 非负实偶且从对称中心向两边非递增;
非负实偶且从对称中心向两边非递增;
 保证滤波器的通带增益为1,即
保证滤波器的通带增益为1,即
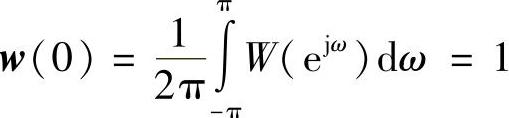
 为保证滤波器相位特性不因加窗而改变,一般要求w恒为正。
为保证滤波器相位特性不因加窗而改变,一般要求w恒为正。
定义如下三个衡量窗函数性能指标的参数:
1)3dB带宽B,它是主瓣归一化幅度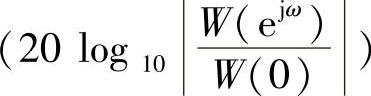 下降到-3dB时的带宽。当数据长度为N时,最大可能的频率分辨率是Δω=2π/N,则B的单位可以是Δω。
下降到-3dB时的带宽。当数据长度为N时,最大可能的频率分辨率是Δω=2π/N,则B的单位可以是Δω。
2)最大旁瓣峰值A(dB),A越小表明由旁瓣引起的振荡幅度越小。
3)旁瓣峰值渐进衰减速度D(dB/oct,oct表示倍频程)。
显然,理想窗函数应有最小的B和A及最大的D。典型的窗函数及三项指标含义如图3-4所示。
在MATLAB中有生成矩形窗、三角窗、巴特列特窗、布莱克曼窗、切比雪夫窗、汉明窗、汉宁窗和凯撒窗的函数。下面画出其波形及幅频响应曲线并给出三项指标,同时给出w从0到N-1和从-(N-1)/2到(N-1)/2的解析式,它们分别以n=(N-1)/2和n=0为对称(只讨论N为奇数情形,给出的图形以n=0对称)。
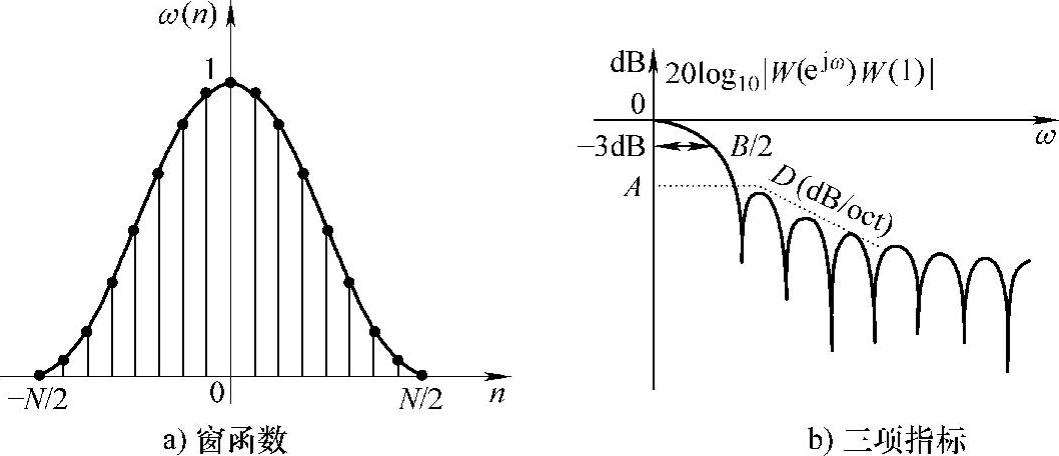
图3-4 窗函数w及性能指标示意
1.矩形窗(Rectangle Window)
w(n)=1,n=0,1,…,N-1
w(n)=1,n=-(N-1)/2,…,-1,0,1,…(N-1)/2
其谱函数为
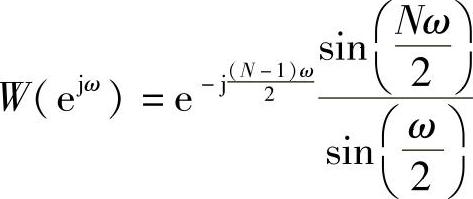
实现w及谱W的MATLAB代码如下:


运行结果如图3-5所示。三项衡量指标分别为:B=0.8872Δω,A=-13.1468dB,D=-13.1777dB/oct。
2.三角窗(Bartlett Window)

或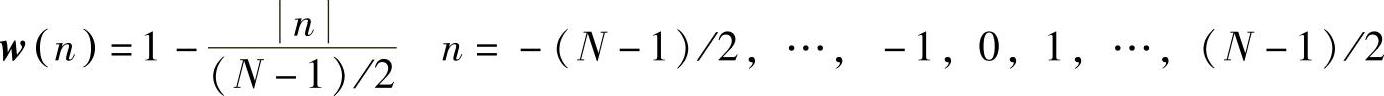
其谱函数为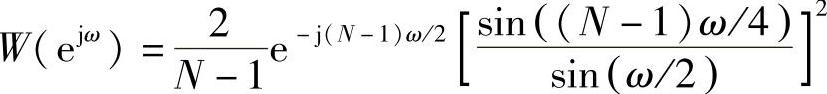
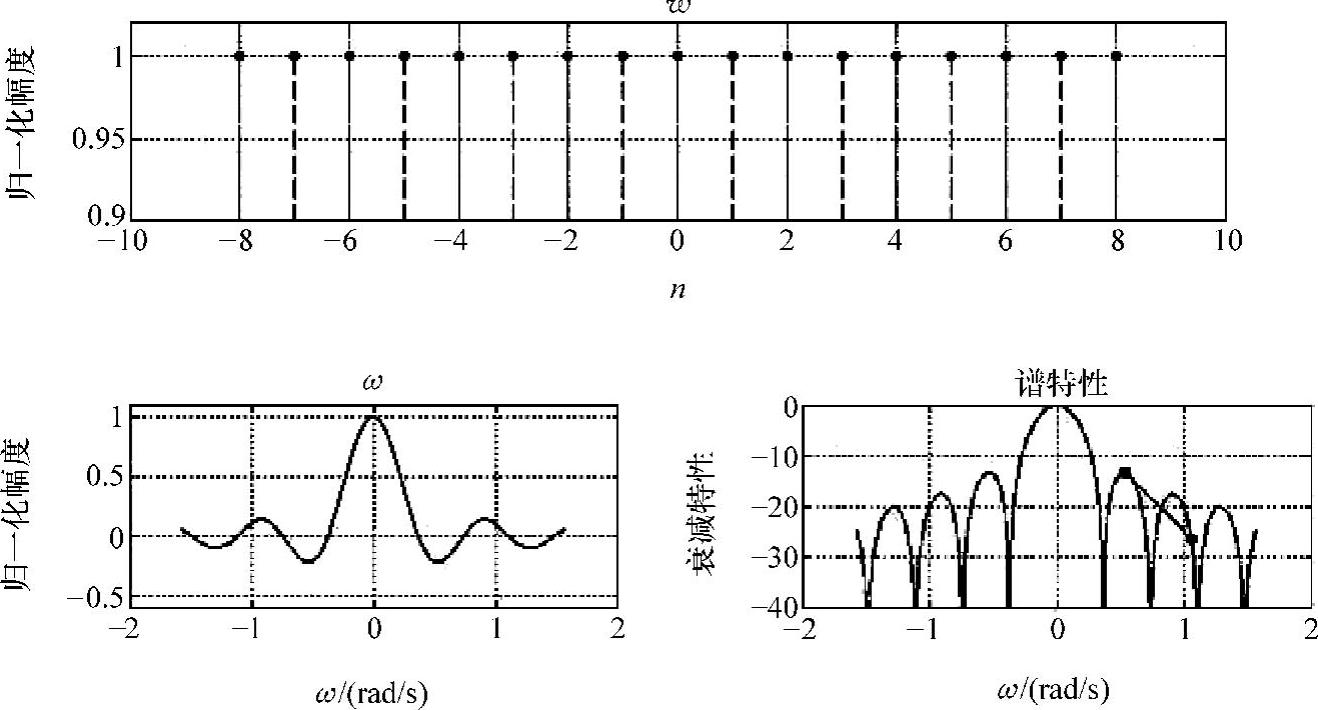
图3-5 矩形窗及谱图
实现w及谱W的MATLAB代码如下(只列出不同部分):

运行结果如图3-6所示。三项衡量指标分别为:B=1.2837Δω,A=-25.7022dB,D=-25.8864dB/oct。
3.余弦窗(Cosine Window)
w(n)=sin[nπ/(N-1)]n=0,1,2,…,N-1
或 w(n)=cos[nπ/(N-1)]n=-(N-1)/2,…,-1,0,1,…,(N-1)/2
其谱函数为
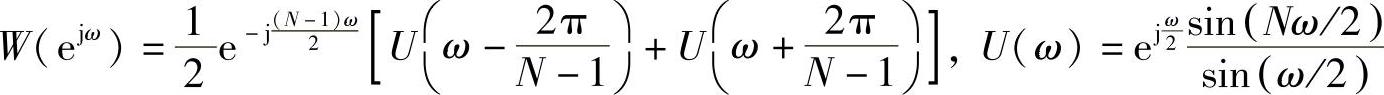
实现w及谱W的MATLAB代码如下(只列出不同部分):

图3-6 三角窗及谱图

运行结果如图3-7所示。三项衡量指标分别为:B=1.2689Δω,A=-22.0788dB,D=-11.2495dB/oct。
值得注意的是,U[ω-2π/(N-1)]和U[ω+2π/(N-1)]的幅值没有共同零点,所以谱W值均大于零,只在两边无穷远处趋近于零。此外,U(ω)含有相位信息,因此谱W整体不具备线性相位。其相位特性如图3-8所示。
4.汉宁窗(Hanning Window)
w(n)=sin2[nπ/(N-1)]=0.5-0.5cos[2nπ/(N-1)]n=0,1,…,N-1
或 w(n)=cos2[nπ/(N-1)]=0.5+0.5cos[2nπ/(N-1)]
n=-(N-1)/2,…,-1,0,1,…,(N-1)/2
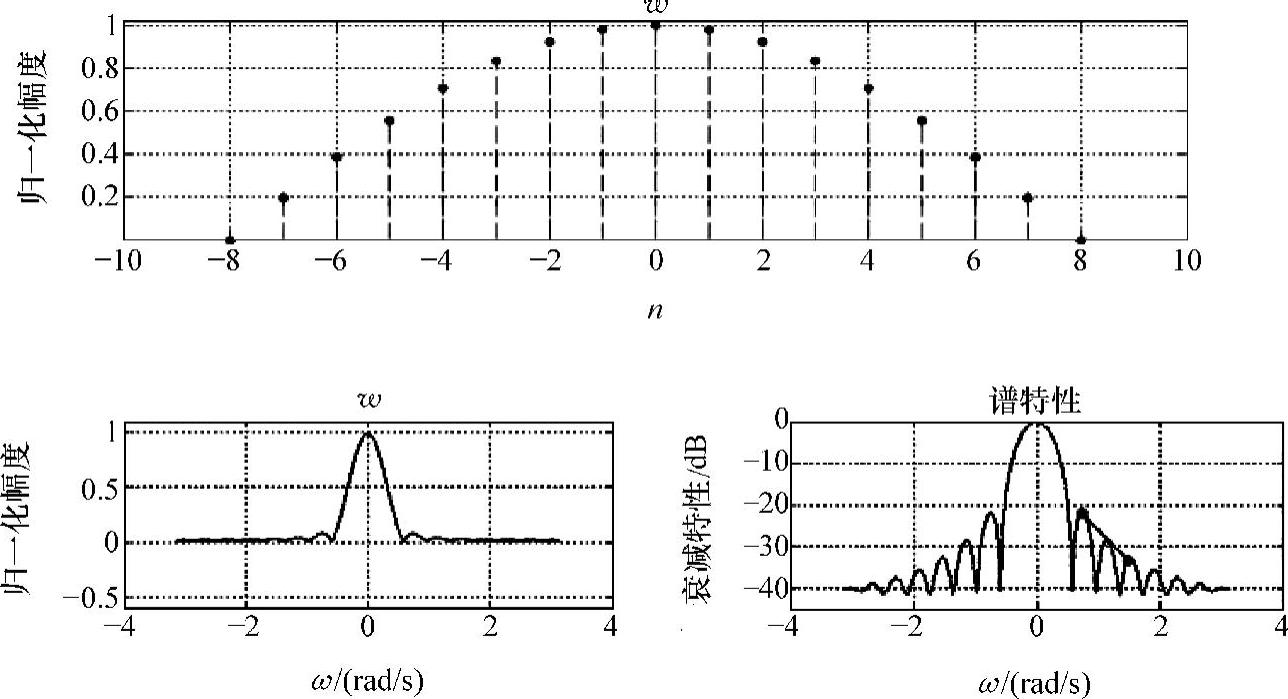
图3-7 余弦窗及谱图
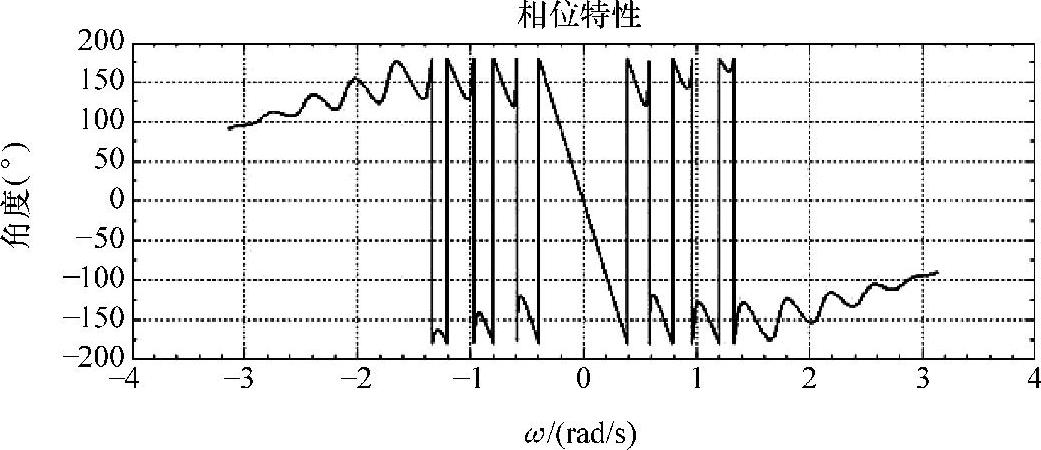
图3-8 余弦窗谱相位特性
其谱函数为
W(e jω)=0.5U(ω)+0.25{U[ω-2π/(N-1)]+U[ω+2π/(N-1)]}
实现w及谱W的MATLAB代码如下(只列出不同部分):


运行结果如图3-9所示。三项衡量指标分别为:B=1.5260Δω,A=-31.4167dB,D=-17.7265dB/oct。同余弦窗的情形相似,其谱没有出现零点。其相位特性如图3-10所示。

图3-9 汉宁窗及谱图
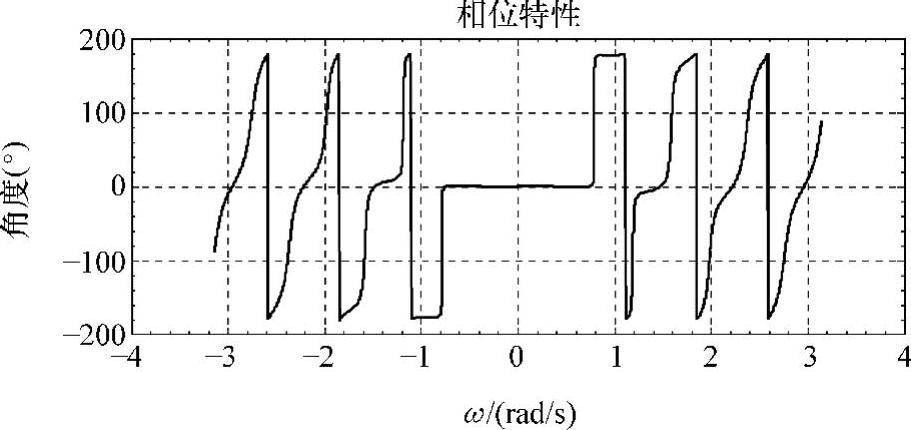
图3-10 汉宁窗谱相位特性
5.汉明窗(Hamming Window)
w(n)=0.54-0.46cos {2nπ/(N-1)}n=0,1,…,N-1
或 w(n)=0.54+0.46cos[2nπ/(N-1)]
n=-(N-1)/2,…,-1,0,1,…,(N-1)/2
其谱函数为
W(e jω)=0.54U(ω)+0.23[U[ω-2π/(N-1)]+U[ω+2π/(N-1)]]
实现w及谱W的MATLAB代码如下(只列出不同部分):

运行结果如图3-11所示。三项衡量指标分别为:B=1.3495Δω,A=-39.0547dB,D=-5.6532dB/oct。同汉宁窗的情形相似,其谱没有出现零点。其相位特性如图3-12所示。

图3-11 汉明窗及谱图

图3-12 汉明窗谱相位特性
6.布莱克曼窗(Blackman Window)
w(n)=0.42-0.5cos[2nπ/(N-1)]+0.08cos[4nπ/(N-1)]n=0,1,…,N-1
或者 w(n)=0.42+0.5cos[2nπ/(N-1)]+0.08cos[4nπ/(N-1)]
n=-(N-1)/2,…,-1,0,1,…,(N-1)/2
其谱函数为
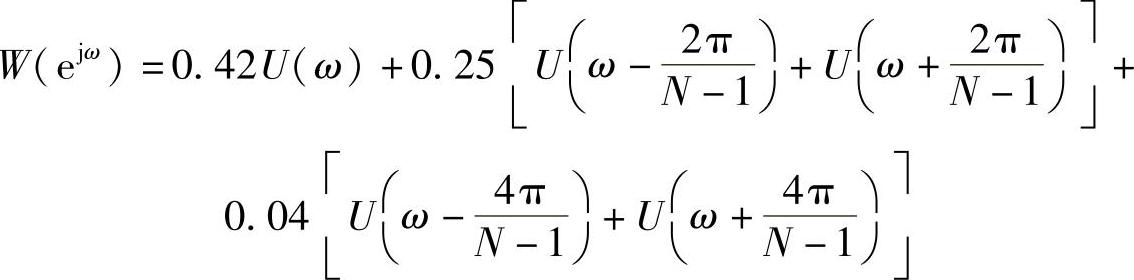
实现w及谱W的MATLAB代码如下(只列出不同部分):

运行结果如图3-13所示。三项衡量指标分别为:B=1.7439Δω,A=-55.2107dB,D=-8.2572dB/oct。同汉明窗的情形相似,其谱没有出现零点。其相位特性如图3-14所示。
7.帕普利斯窗(Papoulis Window)

或者

其谱函数为
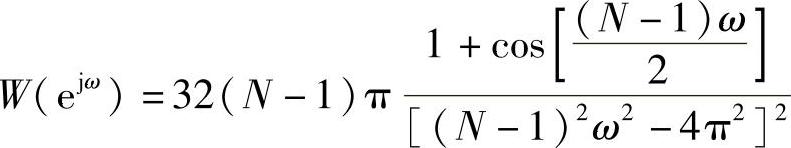

图3-13 布莱克曼窗及谱图

图3-14 布莱克曼窗谱相频特性
实现w及谱W的MATLAB代码如下(只列出不同部分):


运行结果如图3-15所示。三项衡量指标分别为:B=1.6453Δω,A=-46.5291dB,D=-29.1660dB/oct。帕布里斯窗谱出现零点且具有恒定零相位特性。
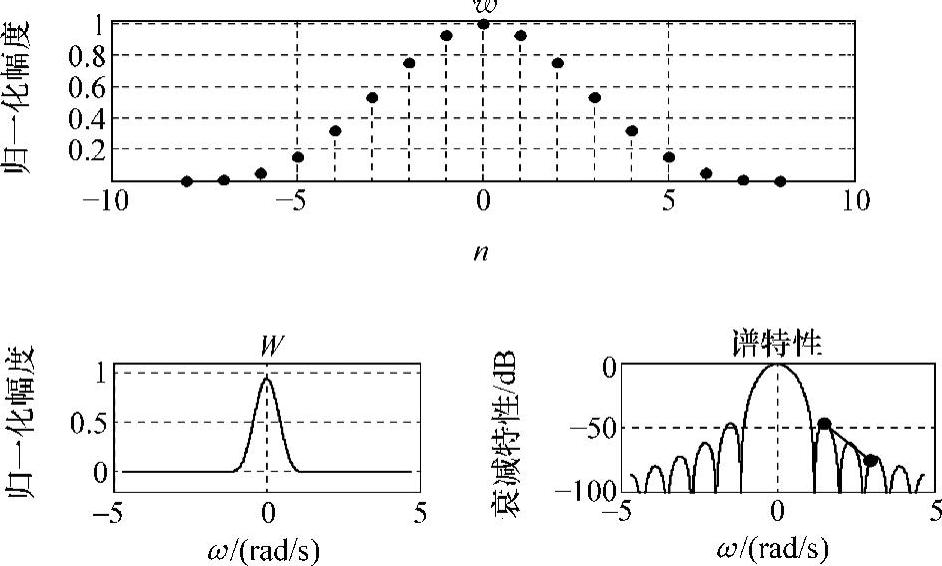
图3-15 帕布里斯窗及谱图
综合以上,矩形窗谱具有最窄的主瓣,但旁瓣峰值也最大;三角窗谱和余弦窗谱主瓣宽度稍宽,但具有较小旁瓣和较大衰减速度。整理各种窗谱指标见表3-1。
表3-17 种窗的4项指标
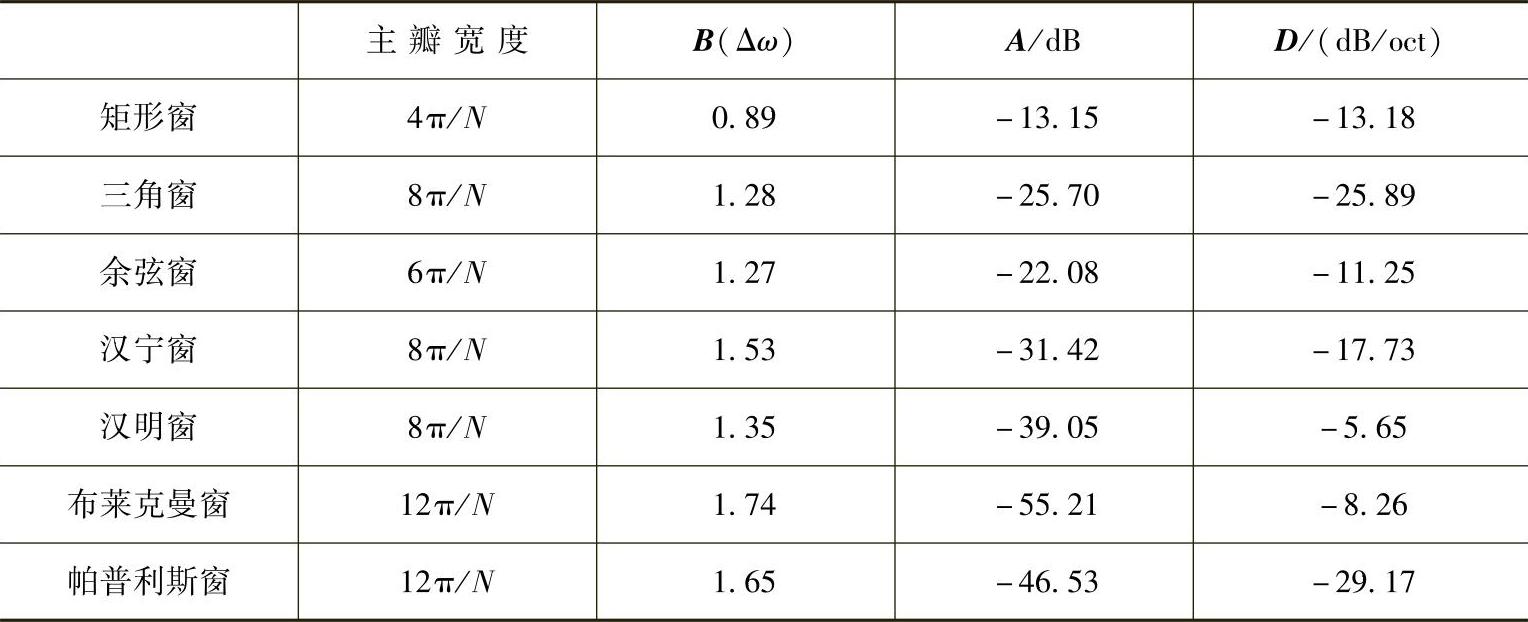
A与B或者D与B在限定算法中基本不能同时改善,为综合衡量窗谱三项指标而定义两个变量:每频率分辨率的最小旁瓣衰减A/B(单位是dB/rad)和每频率分辨率的衰减速度(单位是dB/oct/rad)。它们也分别称为窗口速度和窗口加速度,即

表3-1中七种窗的aw和sw对比图如图3-16所示。

图3-16 七种窗aw和sw
实现图3-16的MATLAB代码如下:

观察图3-16可以发现,布莱克曼窗谱具有最高窗口速度但加速度最小,矩形窗谱窗口速度最小,但加速度大于余弦窗和汉宁窗,三角窗和帕普利斯窗谱的窗口速度和加速度均良好。如果把计算复杂度考虑进去,三角窗是FIR滤波器窗函数设计法中比较好的选择。除上面常见的7种窗外,还有Kaiser窗、Cheby- shev窗、Cauchy窗、Gaussian窗等,它们都可对滤波器性能起到一定的改善作用。
为了得到较好性能的滤波器,在设计时选择合适的窗函数是必要和非常重要的问题。但由于滤波器过渡带带宽与阻带最小衰减相互矛盾,在一定程度上,任何窗函数只能牺牲其中一项指标来换取另一项的改善,同时,滤波器的设计应该结合信号特性和处理目的来进行。
有关全相位数字信号处理方法及MATLAB实现的文章

从形式上看,带参数的宏调用和函数调用没有什么区别,而且确实在一些情况下它们产生同样的结果。例如:程序1:这两个程序的主函数main()是完全一样的,调用宏和调用函数得到相同的运行结果,都是5。理由是使用宏比函数调用更快。因为宏在真正编译之前已被相应地替换,在执行时,不必打断调用程序的运行,也没有参数的传递。......
2023-11-18

晶闸管式弧焊整流器采用电流反馈、电压反馈或电流电压联合反馈,可得到不同的外特性和实现焊接参数的调节,获得所需的调节性能。由于主电路中变压器的漏抗、电抗器及电路导线电阻等分布参数的压降,使外特性有所下降。......
2023-06-25

2)通带内增加了波动,在ωc-2π/N处出现过冲为0.089的最大正峰。3)阻带内产生了余振,在ωc+2π/N处出现过冲为-0.090的最大负峰。图3-2是当N分别取4、8、16、32时Hdg(ω)和Hg(ω)的波纹变化。图3-3中,当阶数N由24增大到216时,由于旁瓣数量的增加致主瓣能量占比逐渐降低,最大正峰的过冲程度也随着N的增大而逐渐减小,但阶数增大至210以后,过冲程度基本没有再改善。......
2023-06-23

1)h=h,且N为奇数。图2-3 奇长度偶对称h设计FIR数字滤波器特性2)h=h,且N为偶数。MATLAB实现如下:式中,b=2hn=1,2,…图2-6 偶长度奇对称h设计FIR滤波器特性综合以上4种条件对应的FIR滤波器设计,给出这种传统方法的MATLAB实现函数[Hg,φω]=traFIR(h,p)。此函数包含两个输入参数即单位冲击响应h及滤波器类型p,函数的输出为系统的幅频特性和相频特性。此外,此方法得到的滤波器在通带、阻带存在幅度较大的波动,总体性能比较低下。......
2023-06-23

图9-17未调度任务优先级之和比较图9-18总能耗比较图9-19任务调度完成时刻比较由图9-17、图9-18、图9-19可知,在选取的6个仿真场景中,MNSGA-Ⅱ对于目标函数f 1,f 2和f 3的优化效果均优于MOGA,其中未调度任务优先级权值之和的平均值降低了66.77%,总能耗平均值降低了69.73%,任务调度完成用时平均值降低了35.27%。......
2023-07-02

金属的锻造性能是衡量金属材料利用锻压加工方法成形的难易程度,是金属的工艺性能指标之一。金属的锻造性能常用金属的塑性和变形抗力这两个指标来衡量。合金钢中合金元素的含量增多,锻造性能变差。金属组织内部有缺陷,如铸锭内部有缩松、气孔等缺陷,将引起金属的塑性下降,锻造时易出现断裂等现象。......
2023-06-28

对于收敛圆的圆心相同的两个复数项幂级数,它们的四则运算可以像实数项幂级数那样来进行,要根据其系数来确定.对于和、差、积所得幂级数在其公共收敛圆内显然收敛,其收敛半径不会小于所给级数的收敛半径最小的一个.如对乘积运算若上式左端两个幂级数的收敛半径分别为R1和R2,则其积的幂级数收敛半径R >min{R1,R2}.为了说明两个幂级数经过运算后所得的幂级数的收敛半径确实可以大于R1 和R2 中较小的一个......
2023-10-30

偏差的时间范围称为抖动幅度,偏差的时间间隔对时间的变化率称为抖动频率。在数字通信系统中,一般将10 Hz以下的长期相位变化称为漂移,而10 Hz以上的相位变化称为抖动。在多中继长途通信中,抖动具有累计性。抖动的单位是UI,它表示单位:时隙。抖动的性能参数主要有:输入抖动容限、输出抖动、抖动转移特性等。这两个参数分别限制映射复用过程中由于比特塞入调整或指针调整过程中引起的数字信号的抖动。......
2023-06-26
相关推荐