图2-73 种截断长度对应的滤波器特性图2-7是M分别取5、10及20时得到的一截止频率为0.25π低通滤波器的幅频特性曲线。矩形窗函数的频谱有较大的旁瓣,正是这些旁瓣在卷积时产生了吉布斯现象。另外,设计滤波器的任务又增加了窗函数的设计。窗函数法是针对时域幅度的控制,对频域期望的特性不能得到有效控制。通过窗函数使滤波器的波纹数得到了减少,但却增加了过渡带宽度。......
2023-06-23
对信号进行各种处理时,由于受到处理时间和计算机存储容量的限制,实际被处理的只能是有限长度的样本,即原始信号必然要被截短,相当于用矩形窗对信号进行调制,从而导致泄漏误差。设hd是理想低通滤波器的单位冲击响应序列,h是从长度为N的矩形窗口RN看到的一段序列(即hd=h·RN),则滤波器频谱为
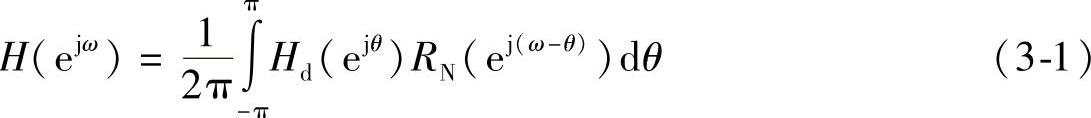
式中,Hd(ejω)和Rd(ejω)分别是hd和RN的傅里叶变换。矩形窗谱函数等于:
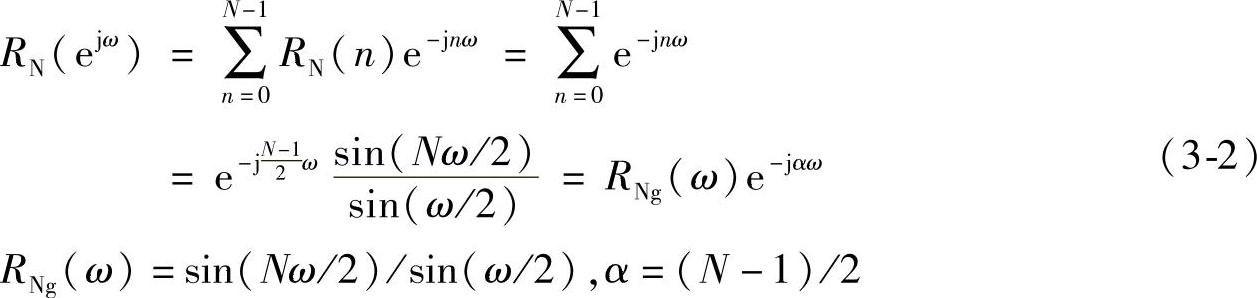
线性理想的低通滤波器Hd(ejω)=Hdg(ω)e-jαω,幅频特性Hdg(ω)满足:
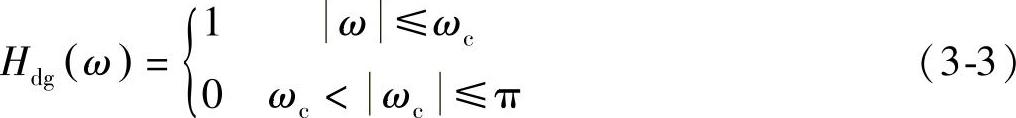
把式(3-2)和式(3-3)代入到式(3-1)得到:

式(3-4)说明滤波器幅频特性等于理想低通滤波器幅频特性Hdg(ω)与矩形窗幅频特性RNg(ω)的卷积,形成过程可简单地由图3-1来描述。
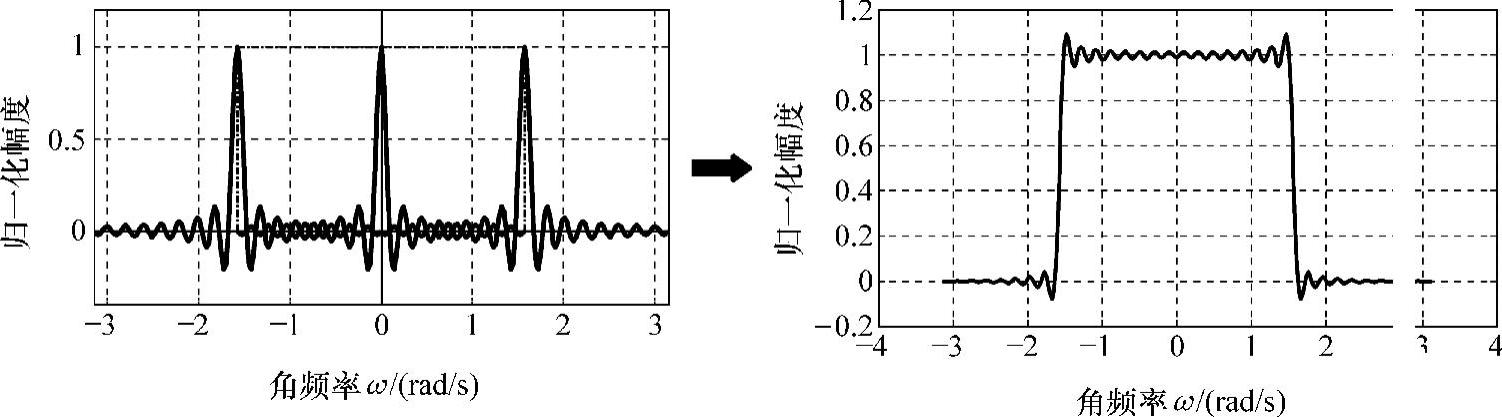
图3-1 卷积过程构造的低通滤波器
实现上述结果的MATLAB代码如下:


当ω=0时,H(0)为图3-1中当RNg(ω)处于Hdg(ω)中央位置时两者乘积的积分,相当于对RNg(ω)在[-ωc,ωc]之间波形积分;当ωc≥2π/N时,此结果近似在[-π,π]之间波形积分,将H(0)值归一化到1;当ω等于截止频率ωc时即图3-1左右两个RNg(ω),积分近似为一半波形积分时,相对H(0)归一化后的值为0.5;当ω=ωc+2π/N时,RNg(ω)主瓣完全移到积分区间Hdg(ω)外面,最大负峰完全在区间[-ωc,ωc]中,因此Hg(ω)在该点形成最大的负峰;当ω=ωc-2π/N时,Hg(ω)产生最大正峰。最大正峰与最大负峰对应的频率相距4π/N。通过以上的分析,对hd加窗处理后滤波器幅值特性Hg(ω)与原理想特性Hdg(ω)的差别主要有以下几点:
1)ωc附近产生宽度约为4π/N即主瓣宽度的过渡带。
2)通带内增加了波动,在ωc-2π/N处出现过冲为0.089的最大正峰。
3)阻带内产生了余振,在ωc+2π/N处出现过冲为-0.090的最大负峰。
4)Hdg(ω)波动愈快(N加大时),Hg(ω)通带和阻带内波动愈快;
5)Hdg(ω)旁瓣大小直接影响Hg(ω)波动大小。
图3-2是当N分别取4、8、16、32时Hdg(ω)和Hg(ω)的波纹变化。
以上五点就是所谓的吉布斯(Gibbs)效应,它直接影响滤波器性能。通带内波动影响滤波器通带平稳性,阻带波动影响阻带最小衰减,同时滤波器一般都要求过渡带越窄越好。增加N可有效地控制过渡带宽度,但并不是减少吉布斯效应的有效方法。通过以下实验可证实此结论,研究当Hdg(ω)的主瓣右零点处于矩形窗右边界点作为右移动起始位置,以频率分辨率2π/N为步长,则Hdg(ω)主瓣及单边各个旁瓣的谱面积(有负值)之和即为最大正峰、过渡点、最大负峰及各个阻带波纹的幅度。同时,还可统计阶数N变化时最大正峰值和主瓣能量占比的变化规律。
图3-3中,当阶数N由24增大到216时,由于旁瓣数量的增加致主瓣能量占比逐渐降低,最大正峰的过冲程度也随着N的增大而逐渐减小,但阶数增大至210以后,过冲程度基本没有再改善。实现上面结果的MATLAB代码如下:
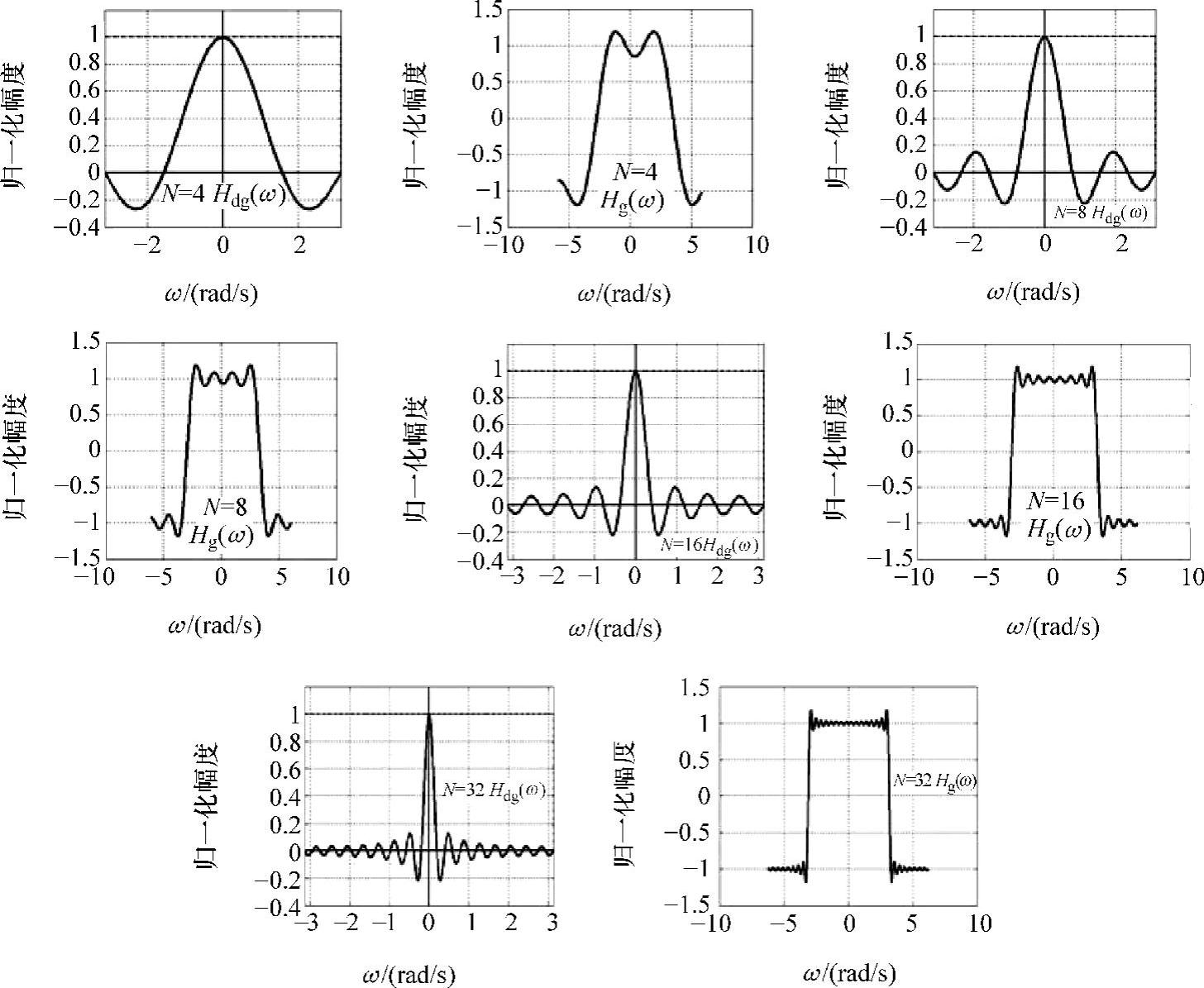
图3-2 不同阶数引起的波纹数变化

图3-3 主瓣及旁瓣能量分布和阶数N对最大正峰影响



减小通带波动及增大阻带衰减只能从窗函数形状上解决,一般要求窗函数谱主瓣尽量包含较多的能量,相应旁瓣幅度就会相对地减小,从而使通带和阻带波动减小且加大阻带衰减,但会以过渡带加宽为代价。在各种窗函数中,阻带衰减大小和带宽宽度是相互矛盾的,选取和设计中应按实际要求侧重一方。
有关全相位数字信号处理方法及MATLAB实现的文章

图2-73 种截断长度对应的滤波器特性图2-7是M分别取5、10及20时得到的一截止频率为0.25π低通滤波器的幅频特性曲线。矩形窗函数的频谱有较大的旁瓣,正是这些旁瓣在卷积时产生了吉布斯现象。另外,设计滤波器的任务又增加了窗函数的设计。窗函数法是针对时域幅度的控制,对频域期望的特性不能得到有效控制。通过窗函数使滤波器的波纹数得到了减少,但却增加了过渡带宽度。......
2023-06-23

约束又称联系,它是体系中构件之间或者体系与基础之间的连接装置。一种约束装置的约束数等于它使体系减少的自由度数。常见的约束类型有链杆、铰、刚性连接。连接n个刚片的复铰具有2(n-1)个约束。或者说,三个刚片原来共有9个自由度,由于复铰A起着两个单铰的作用,减少了4个自由度,所以,体系最后为5个自由度。因此,一个刚性连接相当于三个约束,能减少三个自由度。图11-8所示的固定端约束也是刚性连接。......
2023-06-16

◇ 一个函数可以有多个return语句,通常放在不同的逻辑分支中,但最终只有一个生效。图7.5.1函数返回值JavaScript不要求函数固定返回数据的类型,因此函数内的每个return语句都可以返回任意类型的数据。图7.5.2多个return语句提示JavaScript函数支持多个return语句,不同return语句不需要统一数据类型,但是这样会造成程序不可控。......
2023-11-08

前期研究中,对面子机制进行了大量研究,形成了面子作用机制模型,但这些模型大都只关注了理论研究,未进行相关实证研究;并且,不同情境下的面子机制也不相同,面子作用机制受到多种因素的影响,但“面子如何起作用”,许多学者只进行了描述层面的细致刻画,因此,需要对面子本身的作用机制,面子是如何作用于个体行为的进行研究,以拓展后续相关研究。......
2023-11-17

如果是极点,指出它的级.解 令ζ = 则由于g(ζ)在ζ = 0解析且g 0,所以ζ = 0是的简单极点,因此z = ∞是f 的简单极点.......
2023-10-30

【主要内容】设f′(x)>0(x∈(a,b))或f′(x)≥0(x∈(a,b),但仅在有限个点处取等号),则函数f(x)在(a,b)内单调增加;设f′(x)<0(x∈(a,b))或f′(x)≤0(x∈(a,b),但仅在有限个点处取等号),则函数f(x)在(a,b)内单调减少.注 (ⅰ)以上结论在a=-∞或b=+∞时仍成立;(ⅱ)当f(x)在[a,b]上连续时,端点x=a,x=b可以并入到f(x)的......
2023-10-27

发动机发生的旋转力(转矩)随曲轴角度发生很大的变化,曲轴不断地进行被扭曲再恢复原状态的弹性变形运动,因此在曲轴周围发生强制扭转振动。此时的发动机转速称为扭转振动的临界转速。③在曲轴系统的耦合器内放入橡胶等弹性体,以改变振动系统。图10-14 防扭转振动的扭振阻尼器......
2023-06-28

图4-30所示为AVR的主要时钟系统及其分布,这些时钟并不需要同时工作。终止CPU时钟将使内核停止工作和计算。I/O时钟还用于外部中断模块。此时钟通常与CPU时钟同时挂起或激活。......
2023-06-26
相关推荐