在COPA方法的基础上，Tibshirani等人在2007年提出的OS方法引入了分位数做启发式规则附加表达值，进行差异表达基因检测。由于差异估算中用正常组样本中值代替了全部数据的中值，ORT方法比COPA方法和OS方法恰当地估计了两组数据的差异。COPA方法和OS方法随差异数目的增加，性能有所降低。Lian在2008年提出的MOST方法隐性地考虑了差异基因表达强度临界值所有可能的取值，通过确定其统计量最大值来确定阈值，从而检测差异表达基因。......
2023-11-21
边界拓展算法：AP滤波器与传统方法比较分析
【摘要】：用64阶ap对四种拓展信号过滤出s0及误差对比如图2-43所示。图2-43 ap四种延拓与传统法恢复信号误差比较由图2-43可看出，四种拓展方式在经历64个采样周期后误差均小于传统方法，其中以奇对称误差最小。图2-43再次证实，ap较好地克服了传统分段引起的“跳跃”问题。
需要注意是64阶ap延迟为63个单位时间，所以r=1时正确结果的开始时刻td=63/6000Hz=0.0105s，图2-40的结果也证实了此结论。即对于长度为L的信号经N阶ap系统处理后，长度将变为L-2N+2。为了减小初始N-1个结果的失真并保持信号实际长度，需要对输入信号作边界扩展的预处理。边界扩展应在输入信号的两端进行，通常有边界重复、周期扩展和对称延拓三种方式，示意图如图2-42所示。
图2-42 四种拓展方式示意图
分别按四种方式对含三种频率成分的复合采样信号进行拓展，其中信号成分s0的初相为π/7，复合信号构成如下：
信号长度取256。用64阶ap对四种拓展信号过滤出s0及误差对比如图2-43所示。
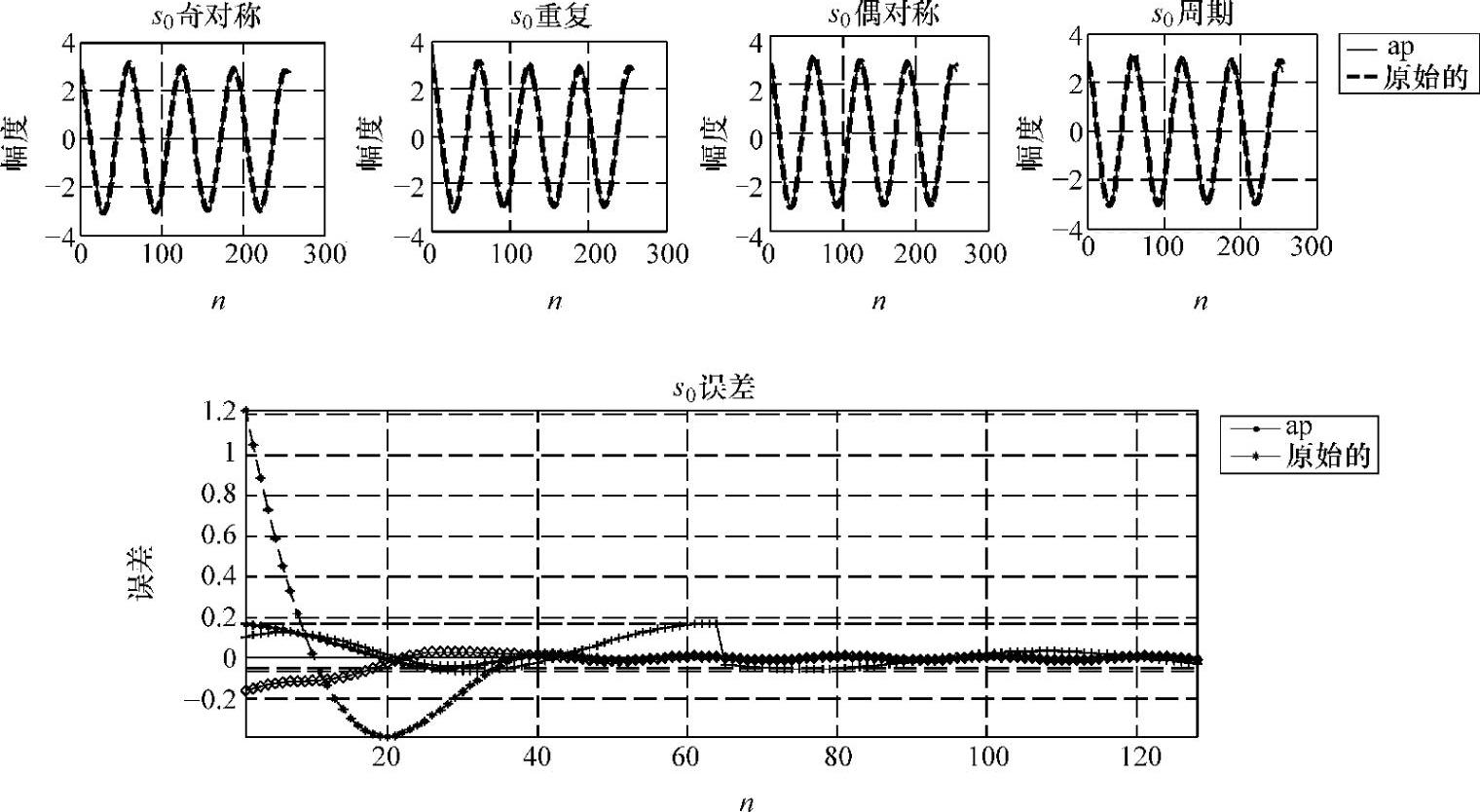
图2-43 ap四种延拓与传统法恢复信号误差比较
由图2-43可看出，四种拓展方式在经历64个采样周期后误差均小于传统方法，其中以奇对称误差最小。图2-43再次证实，ap较好地克服了传统分段引起的“跳跃”问题。采用奇对称延拓ap恢复与传统方法得到的3种分量误差对比结果如图2-44所示。
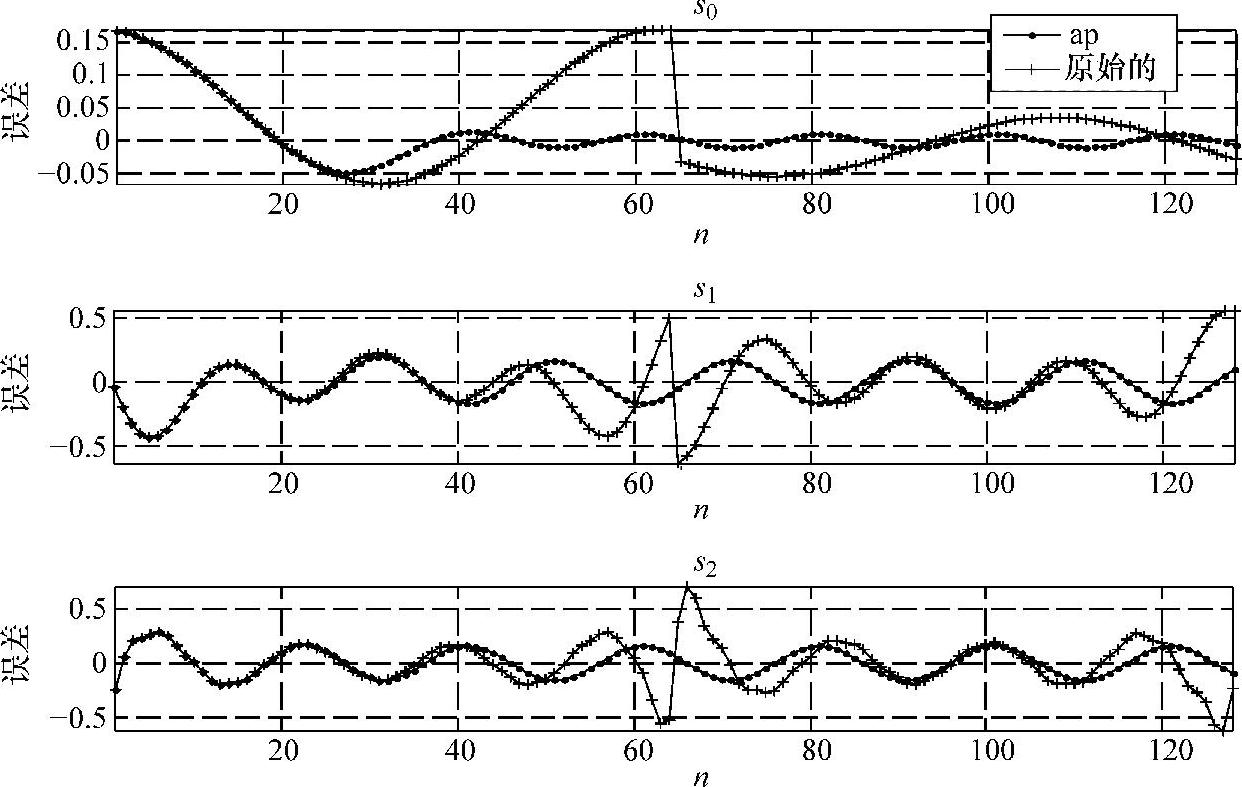
图2-44 ap奇延拓与传统法恢复s0～s2误差比较
实现上面实验的MATLAB代码如下：
有关全相位数字信号处理方法及MATLAB实现的文章
- 详细阅读
-
边界层转捩现象分析与优化方法详细阅读
流体在外部流动时，因为流体的黏性作用层流边界层转换成湍流边界层的现象称为边界层转捩现象，而从层流边界层开始转换成湍流边界层的位置即称为边界层转折点。也就是如果流体发生边界层转捩现象，在转折点xc之前或雷诺数小于临界雷诺数Rce的流体流动形态仍为层流，而在转折点xc之后或雷诺数大于临界雷诺数Rec的流体流动形态视为湍流。......
2023-06-29
-
课程改革研究：观察比较与规律拓展详细阅读
在“只栽一端”和“两端不栽”的情况下，棵数和间隔数之间又有什么关系？［评析］在重点研究了“两端都栽”的基础上，放手让学生自主探索“只栽一端”和“两端不栽”所蕴含的规律，在轻松愉悦的氛围中不知不觉建立了数学模型，对三种不同情况的内在联系与区别有了深刻认识，在数形结合解释规律的过程中，继续渗透了一一对应的数学思想方法。......
2023-11-03
-
传统CLBP算法概述详细阅读
从图4-2可以看出，利用CLBP算法从原始纹理图像中提取的三个分量图像，即符号分量图像CLBPS、幅值分量图像CLBPM和中心像素灰度等级分量图像CLBPC都含有重要的纹理特征信息，联合使用这三个分量图像所含有的特征信息将有助于进一步提高纹理图像的识别精度，这也是CLBP算法的纹理识别性能显著优于传统LBP算法的主要原因。图4-2利用CLBP算法提取纹理图像特征的结果......
2023-06-29
-
聚类算法与特异性发现算法的比较详细阅读
聚类分析发现强相关的对象组，而特异检测发现不与其他对象强相关的对象。图3.8K-means聚类方法与CpecuFind发现特异数据能力ROC曲线K-means聚类；CpecuFind表3.6K-means与CpecuFind发现特异数据能力ROC曲线面积对比上述对比说明，只简单地以簇类大小和对象与类心距离来评估对象的特异程度结果很粗糙，其评价特异数据的能力远不如Cpecu Find方法。......
2023-06-16
-
传统方法FIR数字滤波器设计的MATLAB实详细阅读
1）h=h，且N为奇数。图2-3 奇长度偶对称h设计FIR数字滤波器特性2）h=h，且N为偶数。MATLAB实现如下：式中，b=2hn=1，2，…图2-6 偶长度奇对称h设计FIR滤波器特性综合以上4种条件对应的FIR滤波器设计，给出这种传统方法的MATLAB实现函数[Hg，φω]=traFIR（h，p）。此函数包含两个输入参数即单位冲击响应h及滤波器类型p，函数的输出为系统的幅频特性和相频特性。此外，此方法得到的滤波器在通带、阻带存在幅度较大的波动，总体性能比较低下。......
2023-06-23
-
粒子群优化算法：实用性分析与优化方法详细阅读
粒子群优化算法,是Eberhart和Kennedy[118]提出的一种基于群体智能的优化算法,它是受鸟群和鱼群群体运动的行为方式启发而得到的。这些算法从不同方面对粒子群优化算法进行了改进,不同程度地提高了优化算法的收敛速度和精度,但是效果不是很理想。高鹰等人把混沌思想引入粒子群优化算法中,提出了混沌粒子群优化算法[127-129],取得了良好的效果。因此,本书拟采用混沌粒子群优化算法对风—光—抽蓄复合发电系统进行优化配置。......
2023-06-23
-
新媒体与传统媒体：比较研究与实践详细阅读
社会普遍认为，新媒体的出现影响最大、改变最多的就是传统媒体。人们认为，互联网、手机、车载移动电视、楼宇电视等新媒体传播样式改变了受众的媒介接触行为，对传统媒体领域产生了深远影响。而新媒体时代，传统媒体“把关人”的角色遭到了颠覆和解构。新媒体打破了传统媒体的生存格局，对传统媒体的发展带来了巨大挑战，但传统媒体并未宣告死亡而从此退出历史舞台。......
2023-11-22
相关推荐