二维全相位在各种正交变换的基础上进行了全相位信号处理,一方面扩展了输入信号信息,另一方面对于不同相位信号进行不同权值的加权,从而使二维全相位信号处理在保留传统分块固有性质的同时也具备了一些特殊性质。可把基窗分解成若干个子基窗,从而得到信号不同加权情况下的全相位处理输出,其特性取决于子基窗的形状。以式中低通特性HLL为例,为保持全相位处理的严格零相位特性,仍使子基窗满足中心对称。......
2023-06-23
全相位数字滤波器针对输入的信号进行了N-1/N最大程度重叠,每单位抽样时刻的输入都遍历单位圆上所有相位得到对应的输出,而使频率抽样序列H更准确地控制系统传输特性。如图2-30所示“全相”的示意。

图2-30 “全相”的含义
由等效图2-29可知,单位冲击响应为准2倍周期延拓。对于线性相位系统,则同时满足三种中心对称,即h(0)中心对称、h(0)左右两侧满足h(N-k)=h(k)的对称。加窗使全相位数字滤波器得到极大的改善,卷积窗的设计影响滤波器特性,对于线性相位要求窗必须满足一定的条件。由图2-21看出,对输入信号进行加权重叠(W-O)是新颖的处理方法,它改变了信号某方面特性(如自相关)等,为全相位滤波器特性改善奠定了数据基础。以上这些特征使全相位数字滤波器具有很多重要性质。
定理1:N阶ap系统具有线性相位的充要条件是:H(k)=H(N-k),且对于单窗系统要求非矩形窗中心对称,对于双窗系统要求F=B或者前后窗均中心对称。
充分性证明:由式(2-45)容易推导出ap系统传输特性如下:

因为H(k)=H(N-k),所以h(k)=h(N-k);对于单窗系统f(k)=f(N-1-k),有
C(-k)=f(-k)*RN(k)=f(N-1-k)*RN(k+N-1)=f(k)*RN(-k)=C(k) (2-49)
对于双窗系统若F=B,显然满足C(k)=C(-k);若前后窗均满足中心对称,则有
C(-k)=f(-k)*b(k)=f(N-1-k)*b(k+N-1)=f(k)*b(-k)=C(k) (2-50)
故式(2-48)可以简化为
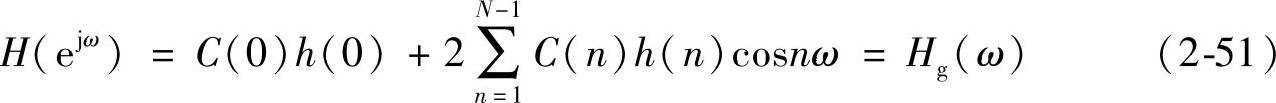
即系统具有严格零相位。若ωk(0≤k≤N-1)表示介于[0,2π]的频率,并记矩阵:
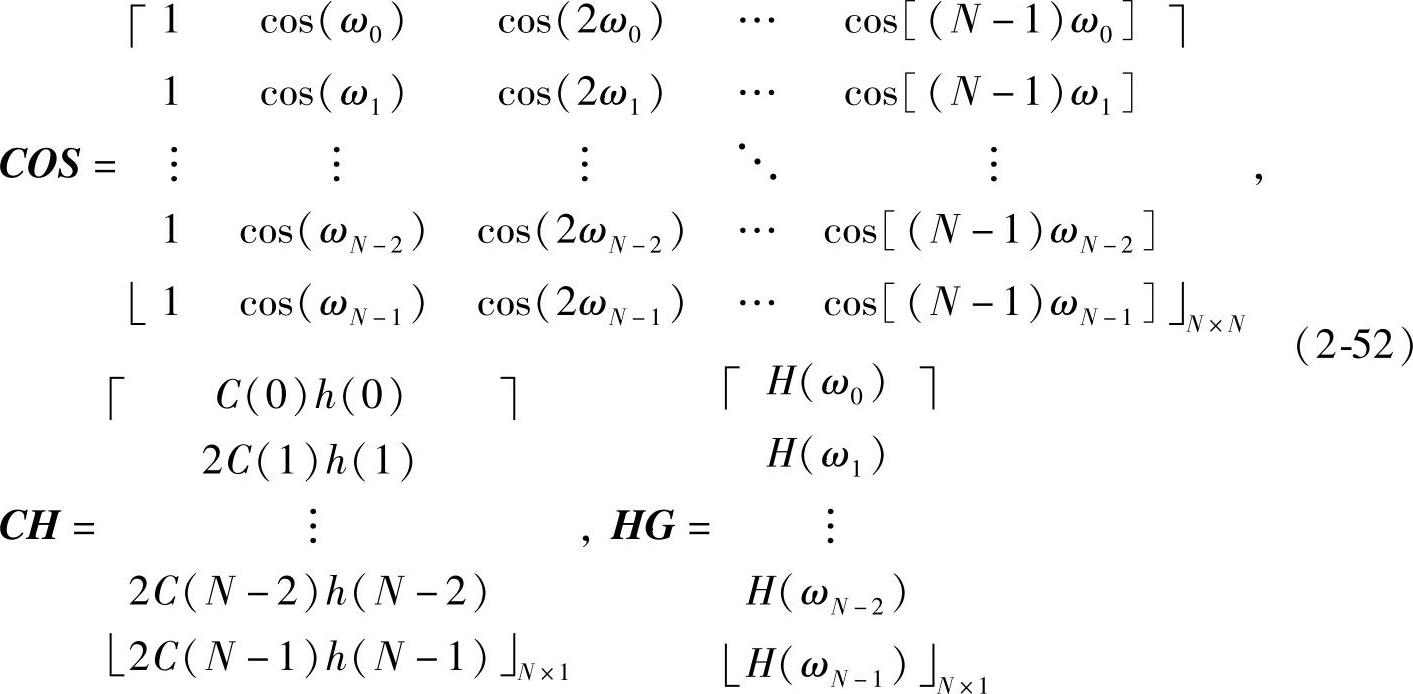
则式(2-51)可以用矩阵表示如下:
COS·CH=HG (2-53)
必要性证明:将具有线性相位的ap系统传输特性写成H(ejω)=Hg(ω)ejφ(ω),并令相位特性φ(ω)=-ωτ。记cn=C(n),将(2-47)式展开并利用h的周期性整理得

τ=0时的系统具有严格零线性相位,正弦函数关于n=0处奇对称,所以上式成立的条件是cnh(n)关于n=0偶对称,即下式对于各种系统恒成立:
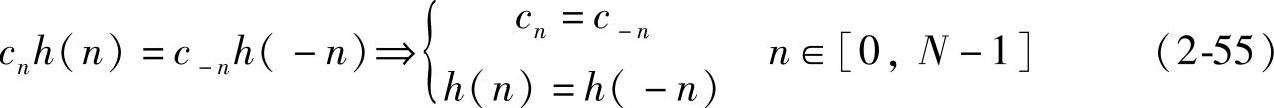
定理1表明,为保证加窗ap系统具有严格零相位,除要求频率抽样序列H具有对称性以外,还要对双窗做出限制:apSW前/后窗具有中心对称性,apDW前后窗相等。在后面的讨论中一般针对线性系统,除非特别指出。按照式(2-53)方式生成ap的MATLAB代码如下:
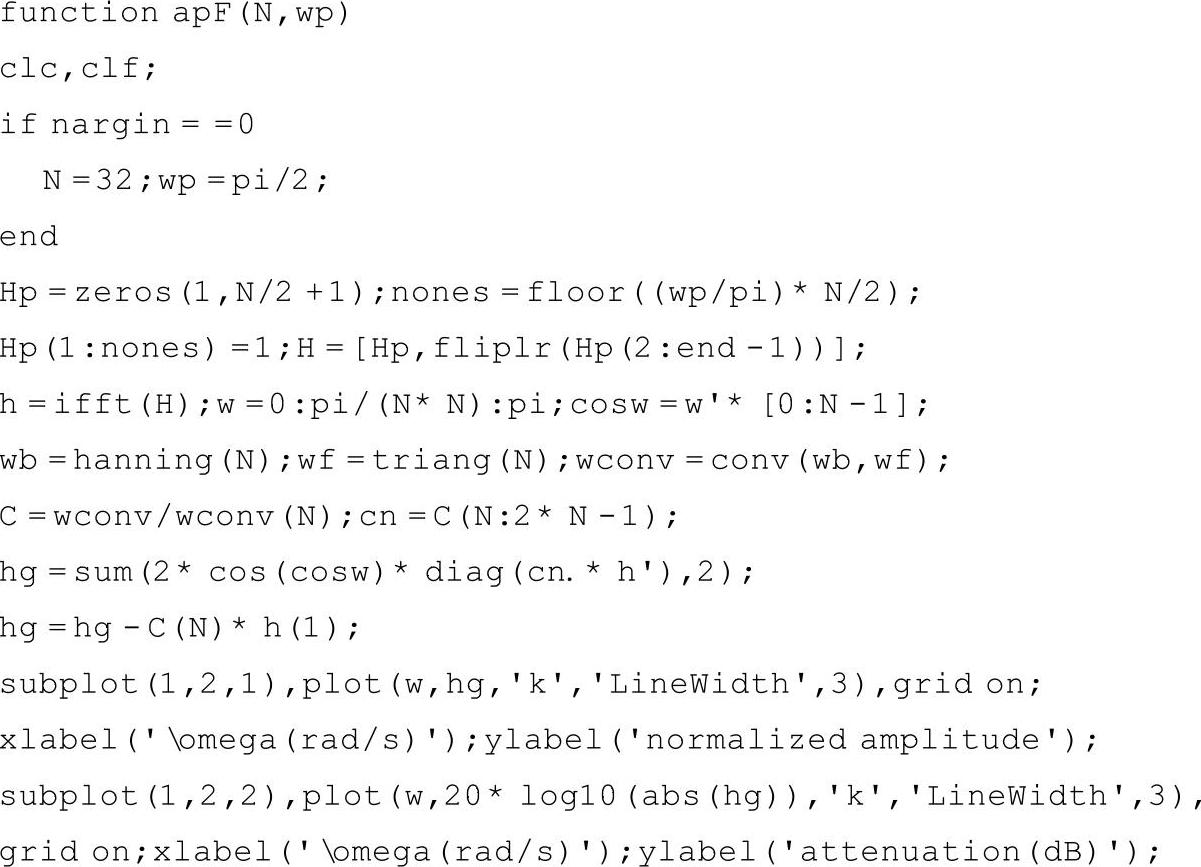
运行结果如图2-31所示。

图2-31 按式(2-52)构造的线性apDW
定理2:N阶线性apNW和apSW系统满足H(ejω)|ω=2nπ/N=H(n)的充要条件是卷积窗1-范数恒等于N,即满足‖C‖1=N;apDW则满足H(ejω)|ω=2nπ/N<H(n)。
证明:ap系统的传输特性可表示如下:

对于apNW和apSW的卷积窗,有

把式(2-57)代入到式(2-56)得到

对于apNW和apSW窗序列‖f‖1=1就能满足定理2的条件。但是,对于apDW的卷积窗元素:

定义频偏向量如下:
cn+cN-n=En (2-60)
式中,En反映了系统特性在频率取样点的偏离程度,只要En具有恒定值就可保证两者相等,而En波动越大代表特性曲线偏离采样点程度越大。apDW的卷积窗元素之和显然为n的函数,为使En平稳而应满足条件:

即要求前后窗相当且具有中心对称特性。结合式(2-61)和式(2-59)可得:

En关于中心对称,最大值在n=0时获得且等于前窗的自相关。由于窗序列f中心能量最大,在对称区间内En单调递减,故用E0归一化后的En只在n=0处等于1,其余各点都低于1,即H(ejω)|ω=2nπ/N<H(n)。
定理3:N阶ap系统频率响应函数等于频率采样向量与卷积窗的离散卷积。即频率响应函数可通过频率采样序列内插实现,其内插函数为卷积窗谱函数。
证明:由式(2-48)可得到:
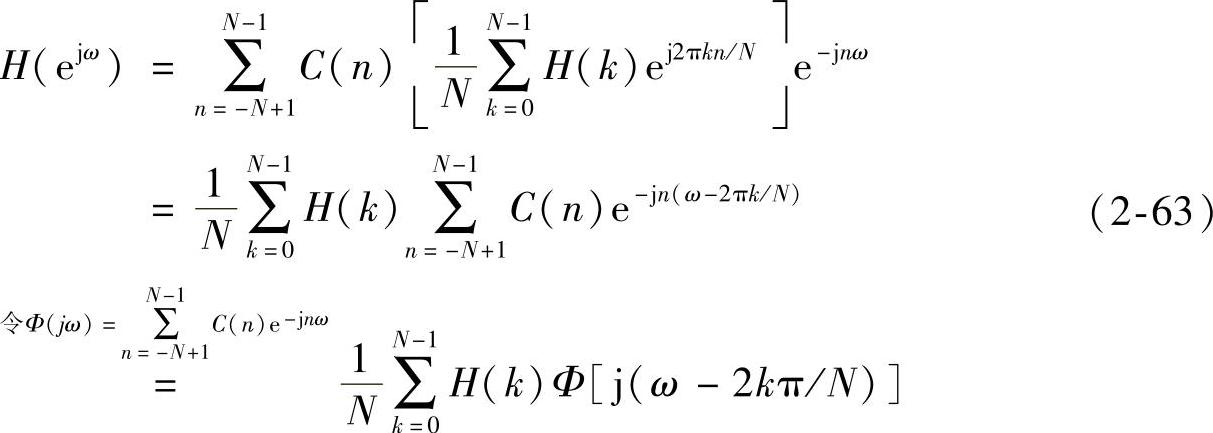
对于N阶传统频率采样法得到的频率响应函数为
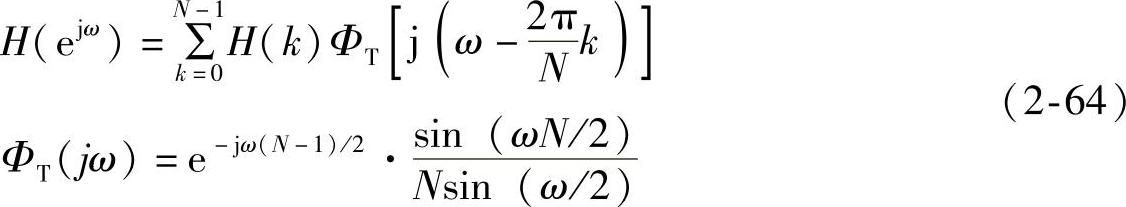
apNW的前后窗均为长度为N的矩形窗,其卷积窗频谱如式(2-64)即ap- NW卷积窗谱ФN(jω)是ФT(jω)的幅频二次方,使旁瓣能量进一步降低而主瓣的能量占比提高。

MATLAB实现两种谱插值函数代码如下:

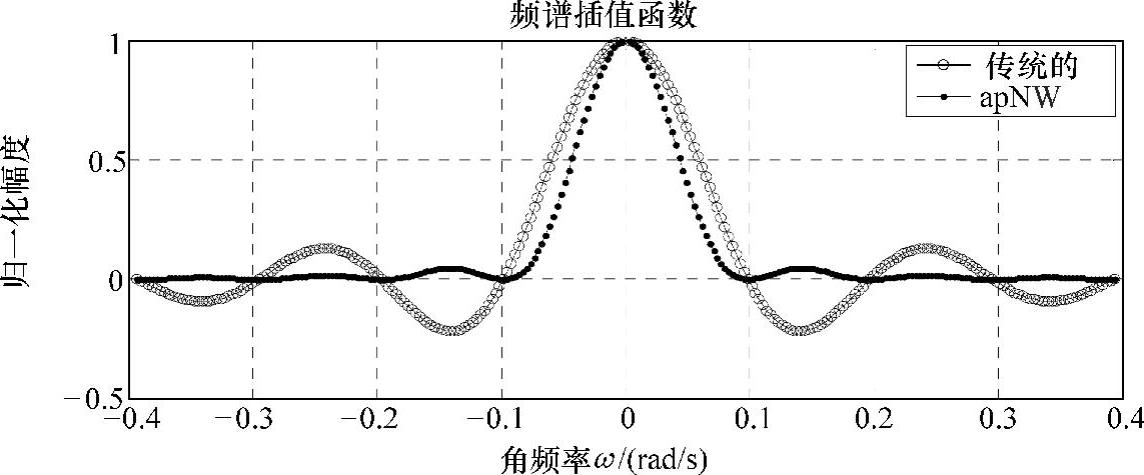
图2-32 apNW与频率采样频谱插值函数对比图
运行结果如图2-32所示。从图2-32可以看出,apNW的卷积窗谱具有以下几个特点:一是谱为实数,由式(2-47)可知是矩形窗谱共轭相乘的结果,因此由式(2-64)内插得到的apNW系统谱也为实数;二是谱为非负数,且旁瓣幅度衰减速率随偏离距离增大而加剧,主瓣占比相对于ФT(jω)提升68%;三是在频率采样点2k′π/N处:

即apNW幅频曲线通过H的频率抽样点,采样点之间的幅度由式(2-64)确定插值函数确定。对于N(奇数为例)阶apSW,其归一化前窗f可以表示为

假设边界点f[(N-1)/2+1]=0,窗f可以表示(N-1)/2+1个变长矩形窗之和,如图2-33所示。
由图2-33可以看出,幅度和长度均可变的矩形窗序列R2n+1中各元素相互正交,即{R2n+1(n)}构成非完备正交系。apSW卷积窗谱可表示如下:
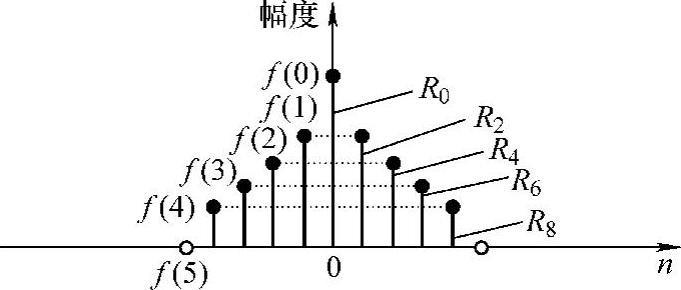
图2-33 apSW前窗矩形基分解图
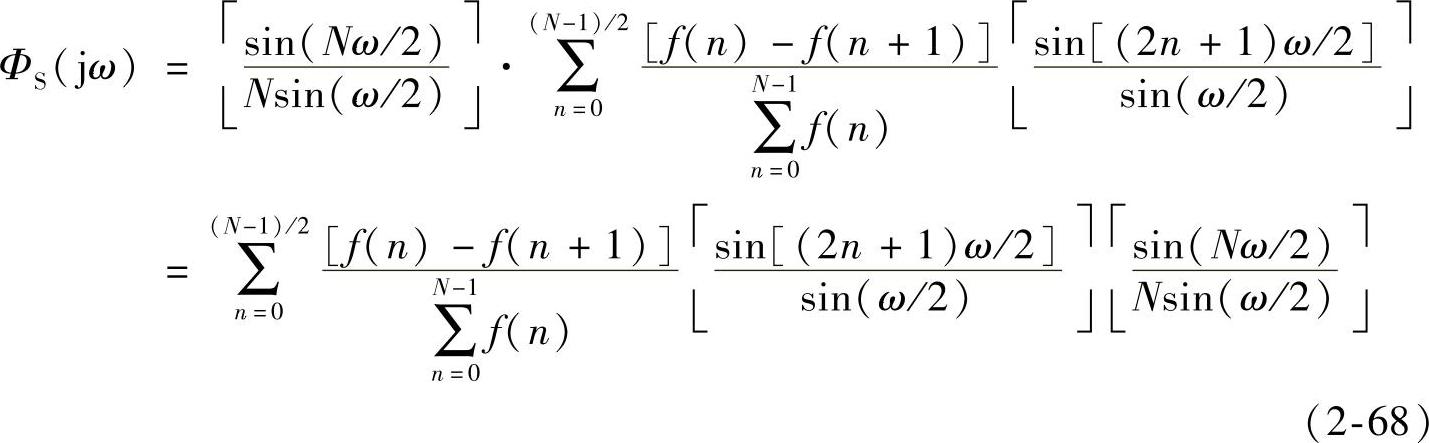
apSW卷积窗谱是N阶矩形窗谱与若干可变长度和幅度的矩形窗谱的积之和。显然,由于增加零值点且可变矩形窗谱的幅度更低而使旁瓣能量比apNW更低,主瓣的能量占比进一步提高;第一零值点仍为2π/N,所以过渡带与频率采样法和apNW相同。在频率采样点2k′π/N处,有
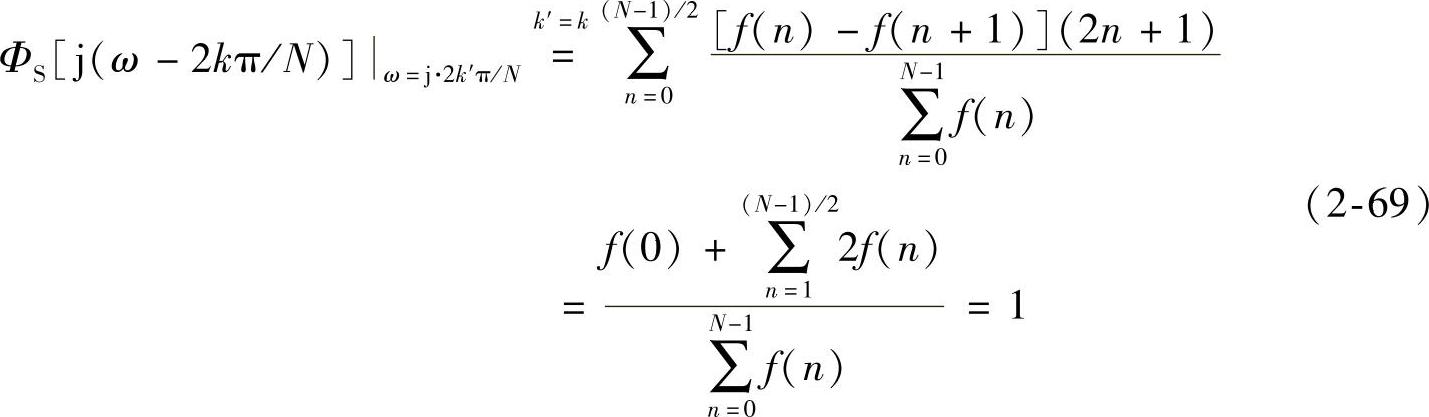
在k′≠k处的Фs(jω)等于0。apSW幅频曲线同样通过H的频率采样点,采样点之间的幅度由式(2-64)插值函数确定。同法可求得N(奇数)阶apDW(前后窗均对称且相等),并注意到{R2n+1(n)}构成非完备正交系,卷积窗谱可表示如下:

在频率采样点2k′π/N处,有
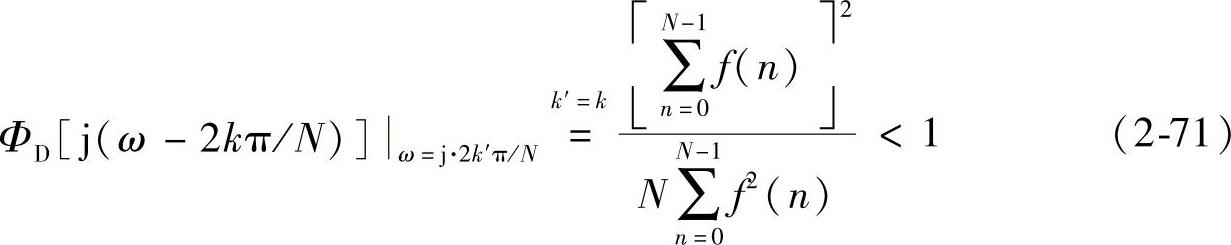
又由于sin[(2n+1)ω/2]/sin(ω/2)≤(2n+1),所以在k′≠k处的频率点卷积窗谱值ФD(jω)均小于1,此结论与定理2是一致的。MATLAB实现的apNW、apSW、apDW卷积窗谱代码如下:


运行结果如图2-34所示。由图2-34可看出,apDW在n=0处幅值低于1。由式(2-71)可知,幅值应该等于长度为8的三角窗所有元素的和的二次方除以元素的二次方和并除以8,结果等于0.7619。图2-34验证了这个结果的正确性。但平移的ФD(jω)序列在n=0处并不为零而将值提升,但始终不能达到1。

图2-34 apNW、apSW和apDW的谱插值函数图
定理4:N阶线性ap系统对卷积窗具有线性性。即如果C=α0C0+α1C1+…αN-1CN-1,yi是对应子卷积窗Ci的输出,则总输出y(n)=α0y0+α1y1+…αN-1yN-1。
证明:对于apDW的卷积窗可以表示如下:
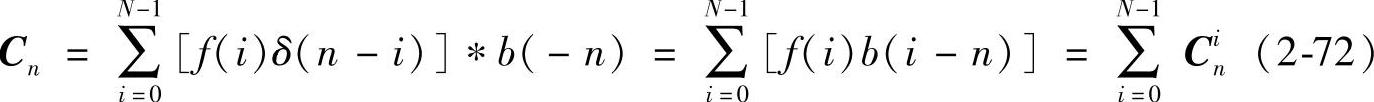
式中
Cni=f(i)b(i-n) (2-73)
即卷积窗可以表示成N个子窗之和的形式,子窗的元素由式(2-73)构成。将子窗的表达形式代入式(2-45)得:

式中,h′(n,i)=Ckih(k)。
由此可知,ap系统卷积窗C分解成N个子窗时,总输出等于N个相应的子输出之和即ap系统对C具有线性可加性。由式(2-72)~式(2-74)推导过程易证明,ap系统对C同样具有线性可乘性,所以ap系统对卷积窗C具有线性性。
设前后窗均为4阶三角窗的ap系统H=[1 1 0 1],单位冲击响应序列h=[0.25-0.25 0.25 0.75 0.25-0.25 0.25],分解得到子窗和子滤波器特性的MATLAB代码如下:


运行结果如图2-35所示。

图2-35 子滤波器幅频/相频及合成特性
分解得到的四个子窗分别为:Cn0=[0.0637 0.1667 0.1667 0.0637 0 0 0],Cn1=[0 0.0637 0.1667 0.1667 0.0637 0 0],Cn2=[0 0 0.0637 0.1667 0.1667 0.0637 0],Cn3=[0 0 0 0.0637 0.1667 0.1667 0.0637];对应的子滤波器的冲击响应为:h′(n,0)=[0.0159 -0.0417 0.0417 0.0477 0 0 0],h′(n,1)=[0 -0.0417 0.1091 0.3273 0.0417 0 0],h′(n,2)=[0 0 0.0417 0.3273 0.1091 -0.0417 0],h′(n,3)=[0 0 0 0.0477 0.0417-0.04170.0159]。由图2-35可看出子滤波器0、3及1、2有相同的幅频特性和互补的相位特性。由式(2-74)可知:
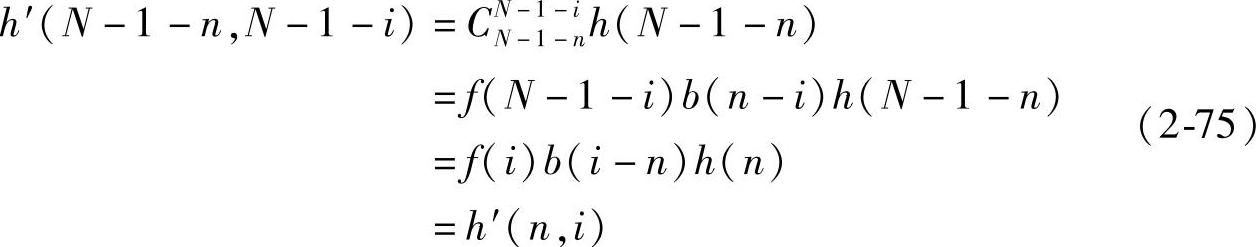
即第i个子滤波器是第N-1-i个子滤波器的镜像,这与图2-35实验结果一致。具有零线性相位的ap分解得到的子滤波器都不再具有线性相位(N为奇数时,仅有中间的子滤波器具有零线性相位),但合成后的滤波器保持严格零相位。
定理5:N阶线性ap系统对频率取样序列H具有线性性。即如果H=α0H0+α1H1+…αN-1HN-1,ym是对应子卷积窗Hm的输出,则总输出y=α0y0+α1y1+…αN-1yN-1。
证明:设系统特性序列H=∑Hm,代入式(2-45)得:

式中,ym(n)是对应子带Hm的输出,即ap系统对H具有可加性且可乘性明显,所以ap系统对频率抽样序列H具有线性性。因此,可用ap进行子带分解,而各个子带应包含信号的全部频率信息而不存在冗余部分即子带间应完全正交。这样,对于N阶DFT域最多可形成N/2+1个(N为偶数)或(N+1)/2个(N为奇数)个严格互补子带:

子带Hm允许通过频率为2mπ/N的信号而抑制其他分量。如4阶全通ap系统H=[1 1 1 1],最大分解得到的三个子带为:低通H0=[1 0 0 0]、带通H1=[0 1 0 1]和高通H2=[0 0 1 0],它们的幅频特性分别如图2-36所示。

图2-36 单频点子带分解图
实现的MATLAB代码如下:

H的分解方式在满足子带正交的条件下是任意的,如可以形成2倍频宽分解方式即Hk宽度2倍于Hk-1。如16阶ap系统2倍频分解得到的4个子带H0=[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0],H1=[0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1],H2=[0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 0],H3=[0 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0],幅频特性如图2-37所示。
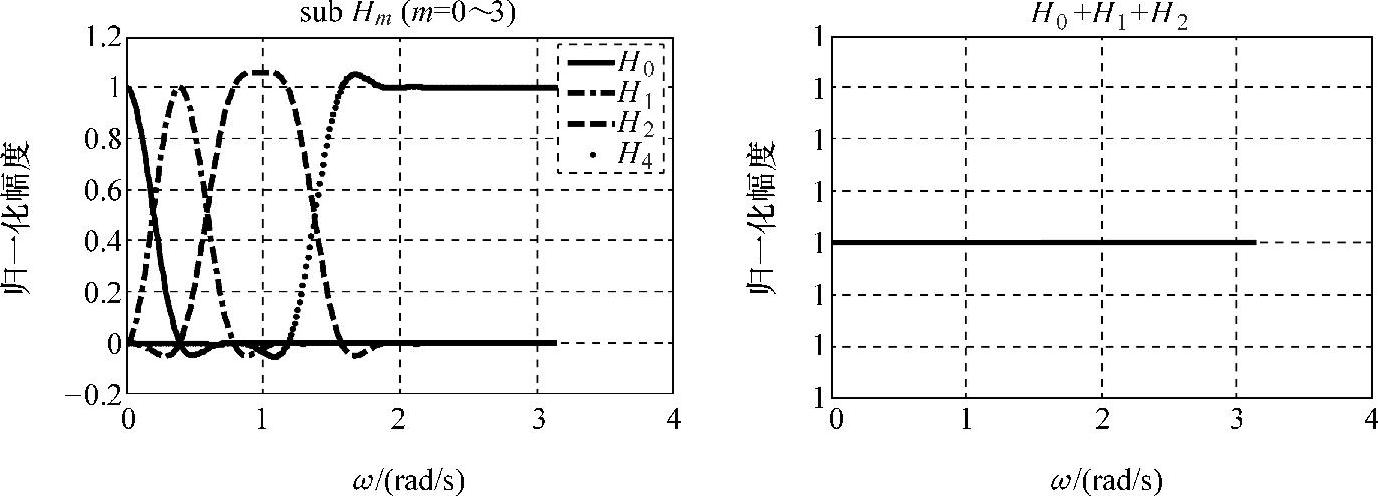
图2-37 2倍频子带分解图
实现代码(只列出Hm形成部分)如下:

为保持各信号分量相对幅值不变可将Hm均设置为1,若要提高或降低某分量可直接将Hm中对应频点设定为变化倍数。对非线性相位ap系统的Hm取值可为复数,它同时对幅度和相位进行调节,如何根据应用需求来设置Hm是值得研究的方向。
定理6:对输入信号进行W-O处理后的相关性降低,卷积双窗降低最大。
证明:由图2-21可知,ap系统对输入信号的W-O处理可用图2-38示意说明。
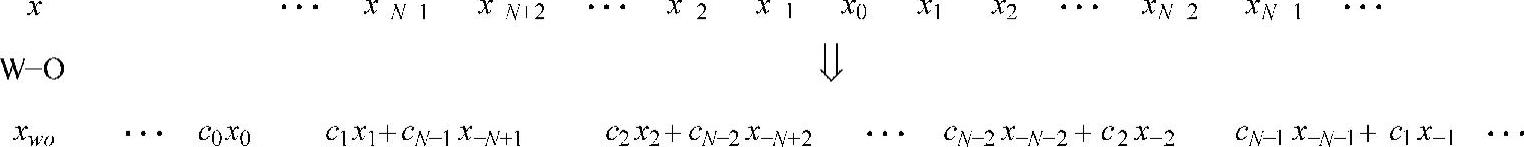
图2-38 W-O处理示意图
无限长序列x的自相关函数可取2N-1长度来进行衡量,并假设相关性平稳(与时间起始点无关),可表示如下:

则序列xwo的自相关函数等于:
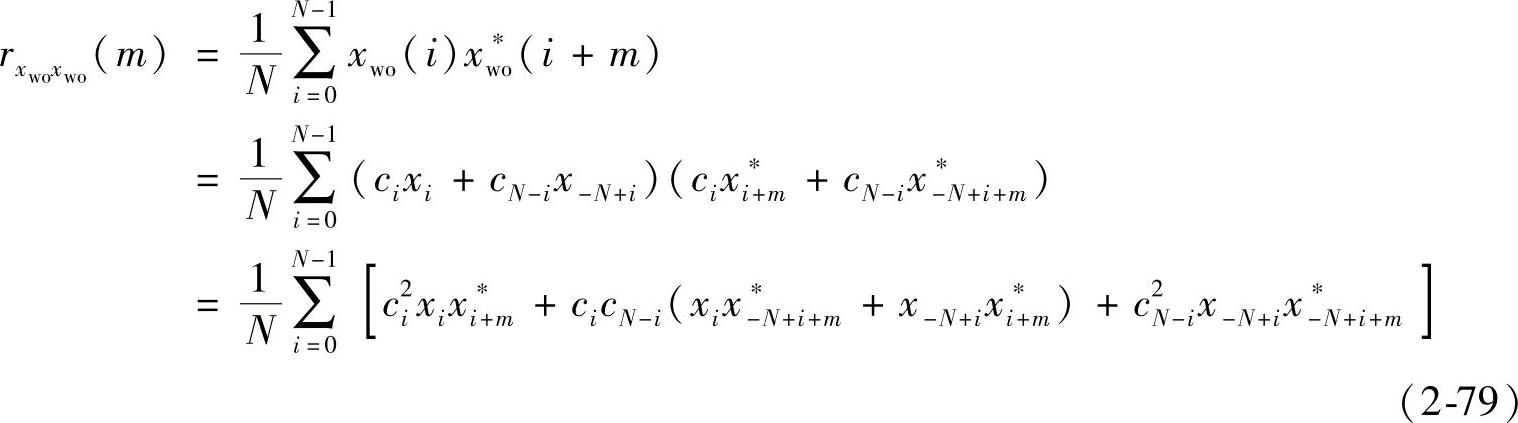
式中,cN=0。
设x为确定复指数信号序列,用最大幅值进行归一化后的元素xi=AWαi+φ,其中W=e-j2π/N,α、φ为实变量。代入式(2-78)并令m=0可得x最大自相关为
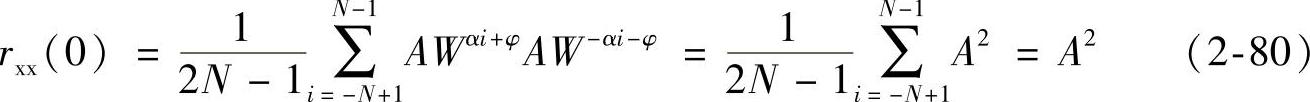
将xi表达式带入式(2-79)并令m=0可得xwo最大自相关:

对于apNW、apSW和apDW的卷积窗都满足ci+cN-i≤1且半带具有单调性。所以xwo最大自相关满足

在式(2-82)中apDW的卷积窗进行了第二次降低。所以,经过W-O处理后的信号相关性都会减弱,降低的最大情况出现在apDW时的卷积窗加权。
假设输入的复信号实部和虚部均是均值为0且方差为1的高斯白噪声,采用N阶进行W-O处理后的信号对比原信号自相关的MATLAB代码如下:

运行结果如图2-39所示。由图2-39可看出,经过W-O处理后的信号自相关性都减少了且apDW降低幅度最大,apNW的降低幅度大于apSW。又由式(2-81)可知,W-O处理后信号自相关最大值是信号频移的函数,因此可用来对信号频率进行校正。
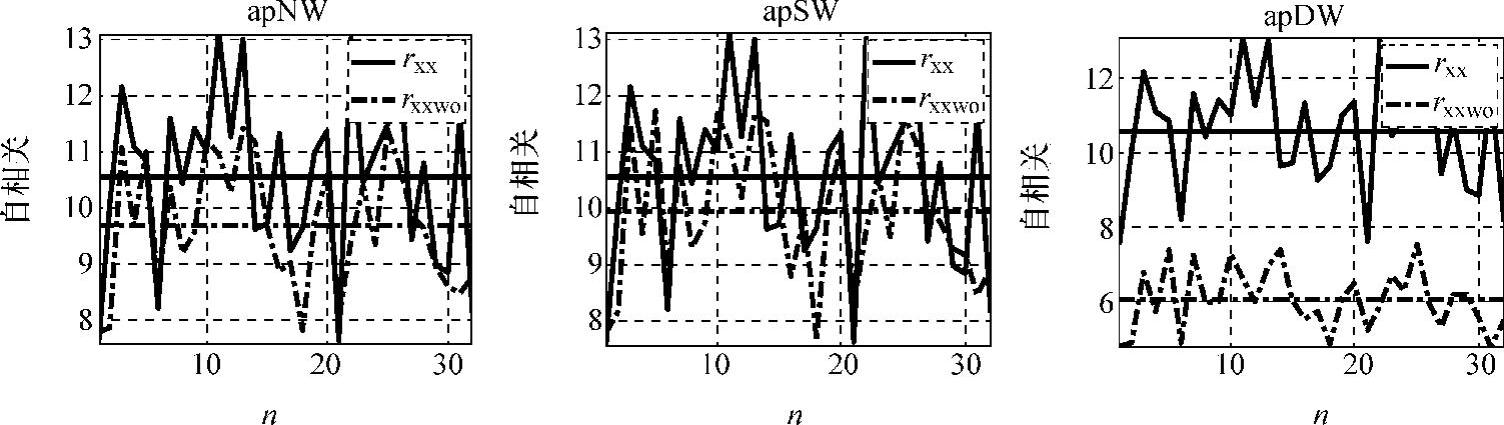
图2-39 W-O处理后信号自相关曲线
有关全相位数字信号处理方法及MATLAB实现的文章

二维全相位在各种正交变换的基础上进行了全相位信号处理,一方面扩展了输入信号信息,另一方面对于不同相位信号进行不同权值的加权,从而使二维全相位信号处理在保留传统分块固有性质的同时也具备了一些特殊性质。可把基窗分解成若干个子基窗,从而得到信号不同加权情况下的全相位处理输出,其特性取决于子基窗的形状。以式中低通特性HLL为例,为保持全相位处理的严格零相位特性,仍使子基窗满足中心对称。......
2023-06-23

为进一步改善系统性能,充分发挥窗函数在滤波器设计中的作用,综合上面两种情形得到在DFT前和IDFT后均加窗的全相位数字滤波器结构如图2-26所示。图2-28 加双窗对比单窗滤波结果对比上面介绍的3种带窗全相位数字滤波器具有完全相同的FIR滤波器等价结构,区别仅仅在于卷积窗的生成方法。为了便于讨论,将第1种类型称无窗全相位数字滤波器,第2种和第3种类型称单窗全相位数字滤波器,第4种类型称双窗全相位数字滤波器。......
2023-06-23

图2-22 加前单窗的全相位数字滤波器记前窗序列为F=[f(N-1)…因此,对比无窗全相位数字滤波器的唯一区别就是卷积窗的大小和形状。从图中可看出,单窗全相位数字滤波器极大地改善了通带及阻带内的波纹数量且降低了波纹幅度,最小旁瓣衰减也降低了6.8dB。图2-23 加前单窗对比无窗全相位数字滤波器特性在MATLAB代码中可以设置不同的窗函数来调整滤波器特性,设置不同的H来对信号进行滤波。......
2023-06-23

即N阶频域全相位滤波器与2N-1阶加三角窗的FIR滤波器等效,此FIR滤波器的单位冲击响应是全相位滤波器特性H的反离散傅里叶变换的两个周期延拓,第一等效图如图2-17所示。图2-17 N阶无窗全相位滤波器第一等效图以下MATLAB代码验证了图2-17与图2-15的DFT域全相位等效。......
2023-06-23

全动床复式河槽由两个对称的滩地及主槽组成,水槽长50m,宽度6m,深1m,由中值粒径为0.8mm 的天然沙均匀构筑而成。图9-20全动床复式河槽初始断面形态全动床复式河槽水槽试验研究:河道完全粗化后能量损失、阻力系数沿程变化,推移质输沙率的变化特性,床沙中值粒径的横向变化与沿程变化等。这种趋势可以表达为图9-21不同坡度的沿程变化归槽水流;漫滩水流图9-23为清水作用下全动床复式河槽输沙率随时间的变化关系图。......
2023-06-22

20世纪70年代初,滤波器组首先在语音编码和多路复用中得到了应用。所谓滤波器组就是将信号按不同的频带分解成一组信号,并将分解得到的子带信号重新合成原信号的处理系统。80年代后期,M.J.Smith等人提出了运用谱分解法设计无失真地重建原始信号的滤波器方法,但存在相位失真。......
2023-06-23

在一维信号处理中,用来抑制噪声干扰并保留原有有用信号的滤波方法以及获得各种信号变换的数字滤波器,有着极其重要和广泛的应用。所以,统计结果表明二维图像信号谱能量90%以上集中在二维低频区域,如果进行2∶1或更高亚取样,谱也未发生重叠。为了克服边缘效应,一种有效的方法是对图像进行重叠滤波,在重叠滤波中的子图像在行列方向上逐点进行重叠。......
2023-06-23

为降低或解决截断误差,国内外有些专家和学者提出了一些改善措施。设输入数据段长度为N1,系统响应长度为N2。全相位滤波法则是使用最大重叠的新方法,它考虑了对某个输入样本的所有长度为N的分段情况,如图1-7所示。图1-6 理想低通滤波器加矩形窗重叠法是由Malvar等人在DCT基础上提出的解决“方块效应”的方法。......
2023-06-23
相关推荐