首页 理论教育DFT域无窗全相位数字滤波器优化方案

DFT域无窗全相位数字滤波器优化方案

2025-09-29 理论教育 版权反馈
【摘要】：即N阶频域全相位滤波器与2N-1阶加三角窗的FIR滤波器等效，此FIR滤波器的单位冲击响应是全相位滤波器特性H的反离散傅里叶变换的两个周期延拓，第一等效图如图2-17所示。图2-17 N阶无窗全相位滤波器第一等效图以下MATLAB代码验证了图2-17与图2-15的DFT域全相位等效。

传统的N阶FIR滤波器某一时刻的输出由该时刻的输入以及它以前的N-1个输入所决定。设系统单位冲击响应为hn=[h（0）h（1）…h（N-1）]T，n时刻输入为xn=[x（n）x（n-1）…x（n-N+1）]T，n时刻的块输出中对应x（n）的输出等于xn与h的循环卷积中对应n时刻的输出，其频域表示如图2-14所示。X和H分别是输入和单位响应的N点离散傅里叶变换。非重叠的滤波输入分段进行，且y（n）只是对应输入x（n）频率为2π（N-1）/N的输出，因此无法求出系统的整体传输特性且输出段与段拼接处会出现不连续的边界效应。

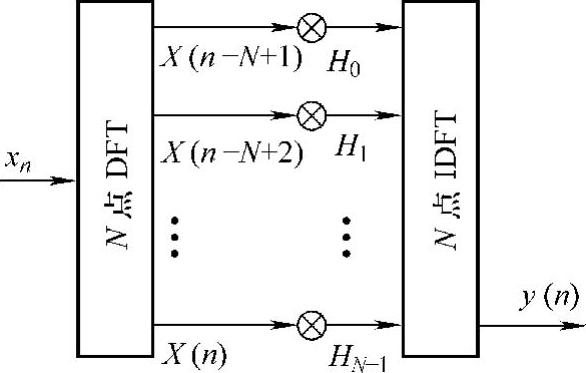
978-7-111-48233-8-Chapter02-59.jpg

图2-14 非重叠频域滤波

全相位滤波器是一个N阶的重叠滤波器，n时刻的输出y（n）是N个相关输入xn+i（i=0，1，…，N-1）块分别对应x（n）的输出响应和的算术平均。设X=[xnxn+1…xn+N-1]是与输入x（n）相关的矩阵，Y=[yN-1（n）yN-2（n）…y0（n）]T是x（n）遍历角频率ω=2kπ/N（k=0，1，…，N-1）时N个输出。N阶傅里叶频域全相位如图2-15所示。

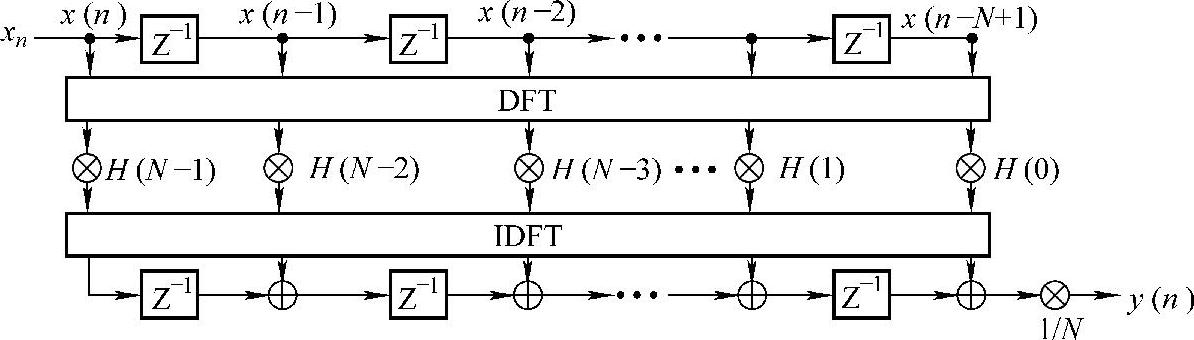
978-7-111-48233-8-Chapter02-60.jpg

图2-15 N阶频域无窗全相位滤波器（ap0）

N阶重叠滤波器在n时刻的输出y（n）是由x（n）以及它前后各N-1个输入决定的，数据关系可表示如下：

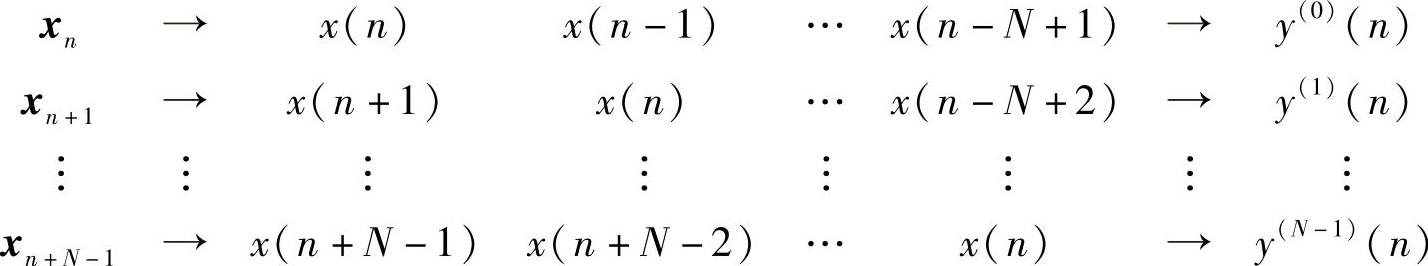
978-7-111-48233-8-Chapter02-61.jpg

设输入信号为频率从-π到π的余弦信号，每次取样256个点，32阶系统特性H=[1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1]。

MATLAB实现代码如下：

978-7-111-48233-8-Chapter02-62.jpg

978-7-111-48233-8-Chapter02-63.jpg

对不同频率的余弦信号经过全相位滤波器处理而产生的输出表明了系统的传统特性，上述算法运行结果如图2-16所示。

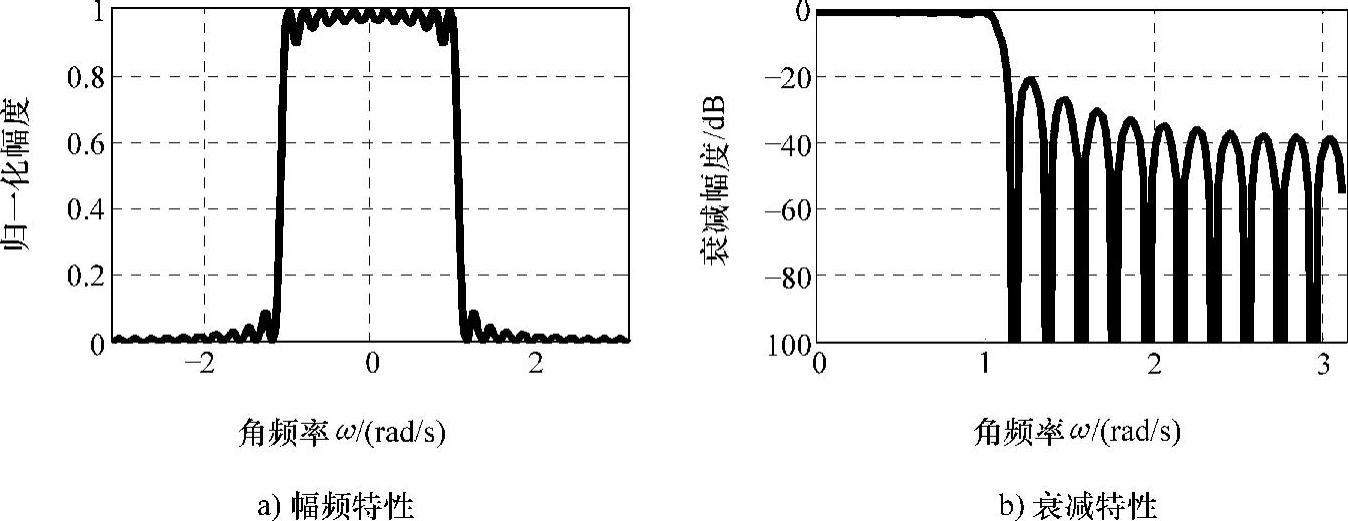
978-7-111-48233-8-Chapter02-64.jpg

图2-16 32阶无窗全相位滤波器特性

全相位系统对频率为0.9817rad/s左右信号进行了选择，通过H的设置可看出，上截止频率也正是2π/32×5≈0.9817rad/s，从而验证了设定为H的全相位系统具有低通特性。现定义抽取算子S=[s0s1…sN-1]T，其中si表示第i个元素为1其余元素为0的列向量。系统频域取样矩阵H=diag（H0H1…HN-1），则图2-15中重叠滤波器的输出为

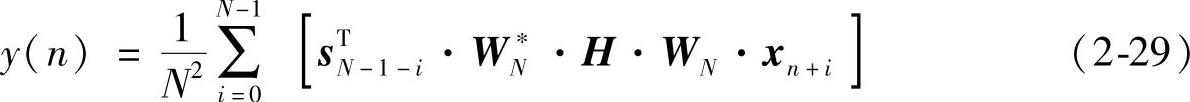
978-7-111-48233-8-Chapter02-65.jpg

式中，WN是N阶傅里叶变换矩阵；WN是WN的共扼。

将式（2-29）展开得

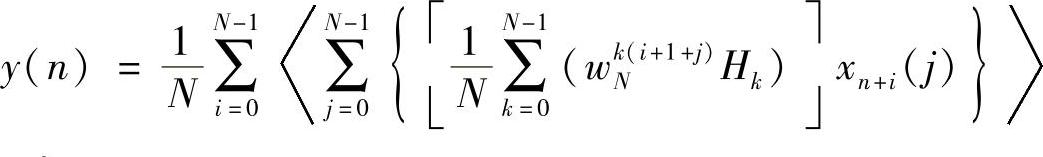
978-7-111-48233-8-Chapter02-66.jpg

式中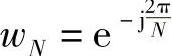，978-7-111-48233-8-Chapter02-67.jpg。注意到：

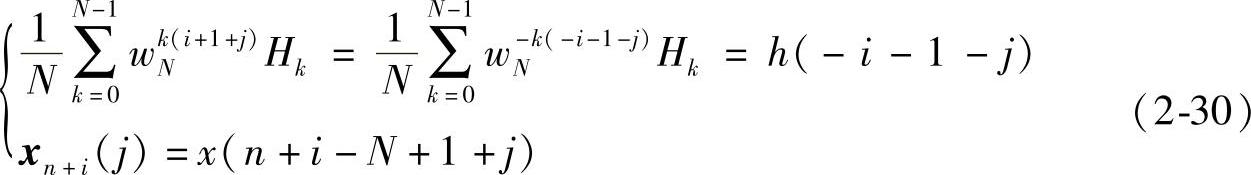
978-7-111-48233-8-Chapter02-68.jpg

将式（2-30）代入到式（2-29）（注意h（n）隐含具有周期N）得

978-7-111-48233-8-Chapter02-69.jpg

即N阶频域全相位滤波器与2N-1阶加三角窗的FIR滤波器等效，此FIR滤波器的单位冲击响应是全相位滤波器特性H的反离散傅里叶变换的两个周期延拓，第一等效图如图2-17所示。它的物理意义是：信号输入序列X中与x（n）有关的N个块xn+i，依次作为冲击响应分别为将h循环右移i位的FIR滤波器的输入，相对应的N个输出之和。

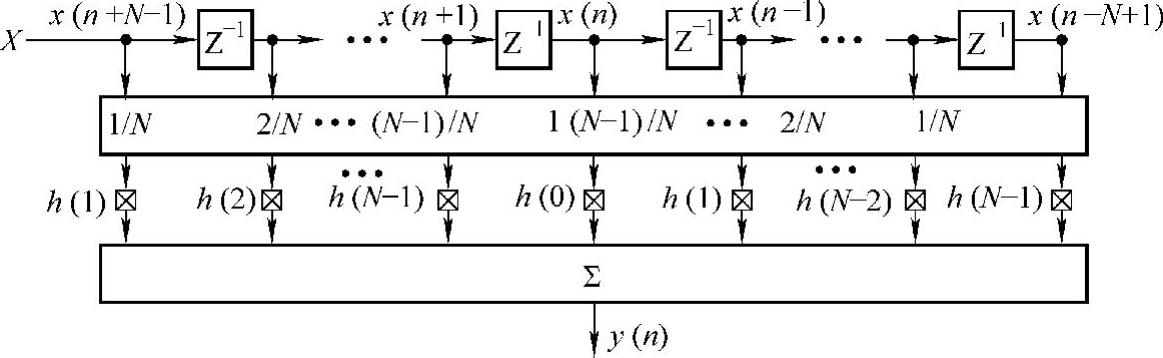
978-7-111-48233-8-Chapter02-70.jpg

图2-17 N阶无窗全相位滤波器第一等效图（ap1）

以下MATLAB代码验证了图2-17与图2-15的DFT域全相位等效。输入信号由f1=16Hz和f2=32Hz的正弦波叠加而成，传输特性选择32阶非对称结构即H=[1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1]。

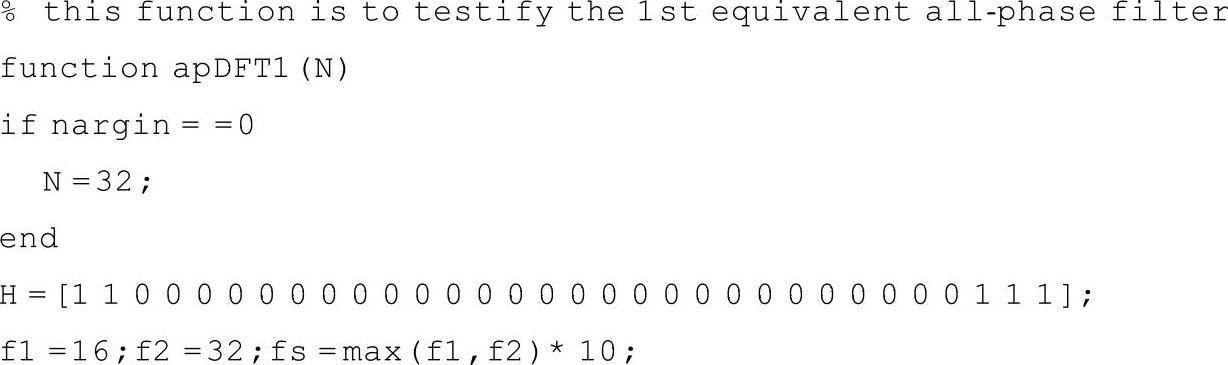978-7-111-48233-8-Chapter02-71.jpg(https://www.chuimin.cn)

978-7-111-48233-8-Chapter02-72.jpg

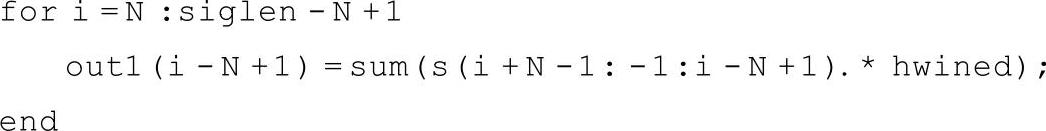
978-7-111-48233-8-Chapter02-73.jpg

运行结果如图2-18所示。

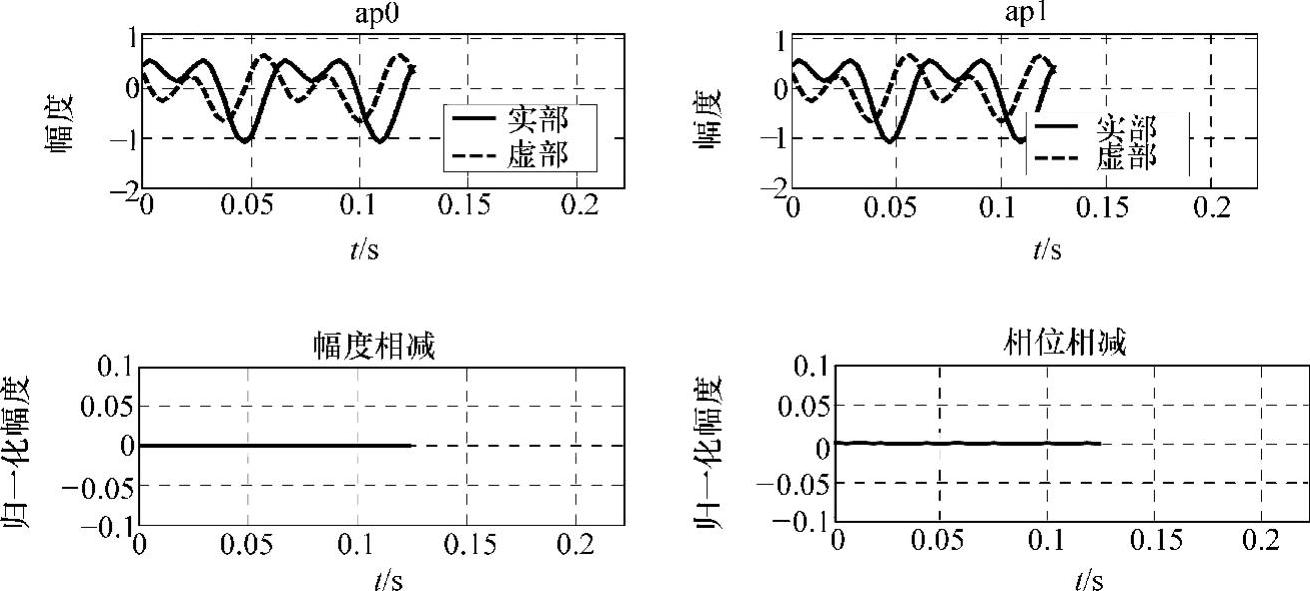
978-7-111-48233-8-Chapter02-74.jpg

图2-18 ap0与ap1等效性验证

由图2-17可知，ap1结构中FIR滤波器单位冲击响应h=[h（1）h（2）…h（N-1）h（0）h（1）…h（N-2）h（N-1）]。利用h的周期性将ap1又可简化为如图2-19所示。

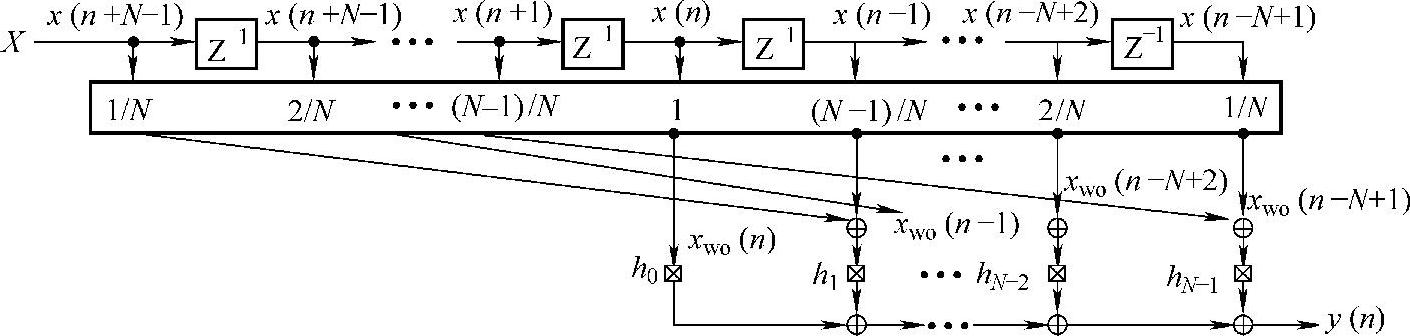
978-7-111-48233-8-Chapter02-75.jpg

图2-19 N阶无窗全相位滤波器第二等效图（ap2）

ap1共用到了延迟单元2N-2个，加法器2N-2个，乘法器4N-2个，但对比ap0省去了DFT/IDFT复数运算；ap2使用延迟单元2N-2个，加法器2N-2个，乘法器3N-1个，对比ap1节省乘法器N-1个。设H=[1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0]，实现ap2的MATLAB代码如下：

978-7-111-48233-8-Chapter02-76.jpg

运行结果如图2-20所示。

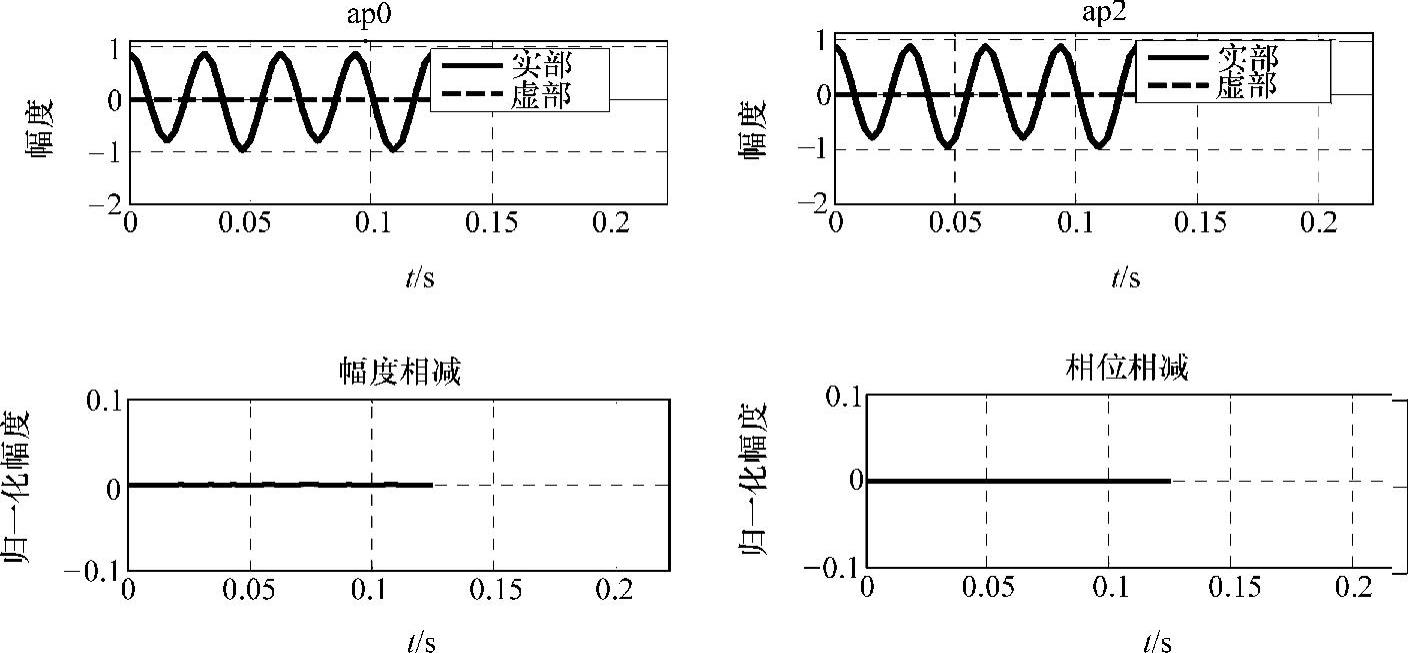
978-7-111-48233-8-Chapter02-77.jpg

图2-20 ap0与ap2等效性验证

由ap0的结构可知，在任意时刻n的输入x（n）都有对应的输出y（n），频率采样序列H具有类模拟系统传输特性。为充分发挥全相位数字滤波器在频域中的滤波作用，利用DFT可得到等效频域结构。令xwo=[xwo（n）xwo（n-1）…xwo（n-N+1）]T，则

xwo=O·C·xn （2-32）

式中，O和C分别称为重叠矩阵和卷积窗，它们有如下形式：

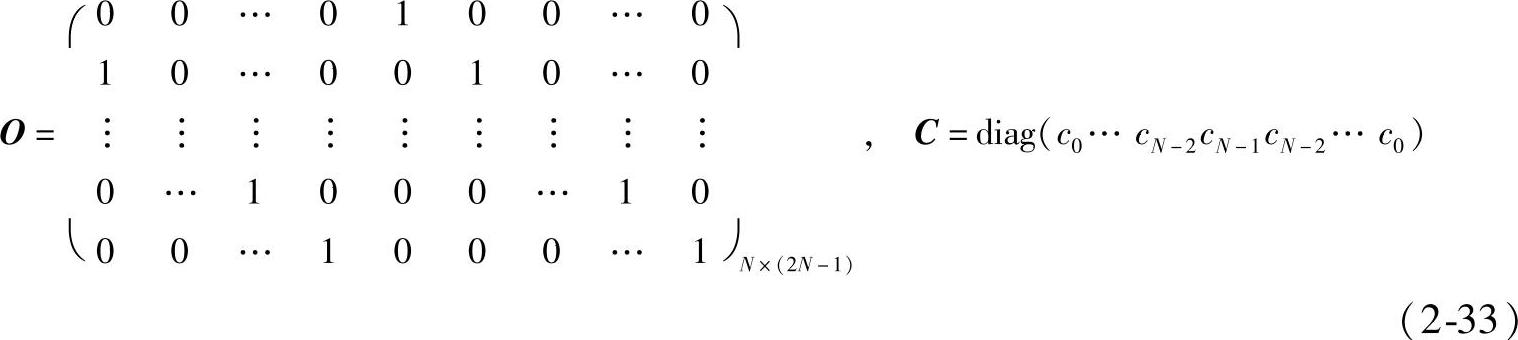
978-7-111-48233-8-Chapter02-78.jpg

无窗全相位数字滤波器的卷积窗元素为

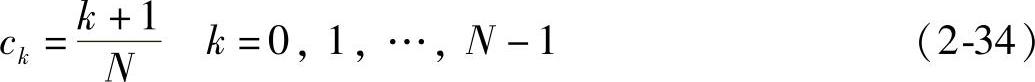
978-7-111-48233-8-Chapter02-79.jpg

图2-19中的输出可表示如下：

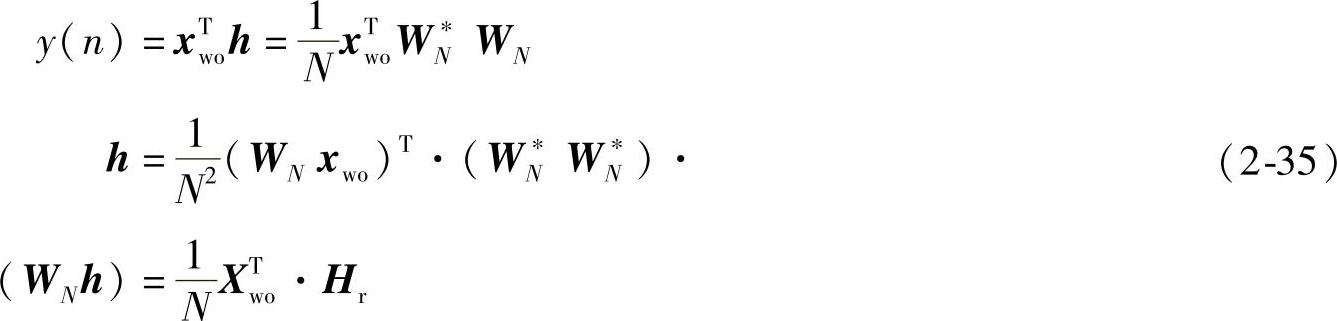
978-7-111-48233-8-Chapter02-80.jpg

式（2-35）中，Xwo是向量xwo的离散傅里叶变换，Hr由下式定义：

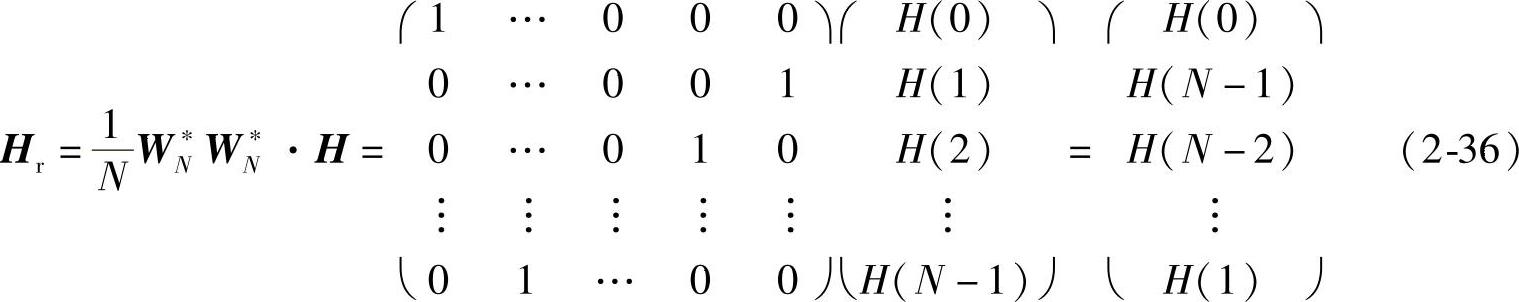
978-7-111-48233-8-Chapter02-81.jpg

式（2-35）就是全相位数字滤波器的频域表达式，其系统结构如图2-21所示。

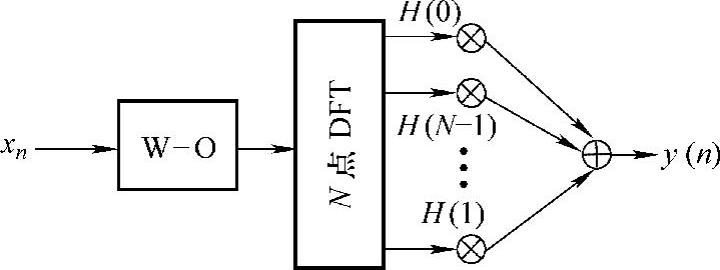
978-7-111-48233-8-Chapter02-82.jpg

图2-21 N阶无窗全相位滤波器第三等效图（ap3）

与图2-15相比，只经过一次DFT但要对输入信号做加权重叠处理。此结构频域滤波器可以通过调节H来有效地控制信号各个频率分量，全相位数字滤波器具有传统频率采样法设计的特征，对原信号加权和重叠处理又兼有窗函数设计法特点。实现ap3的MATLAB代码（设H=[1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0]）如下：

978-7-111-48233-8-Chapter02-83.jpg

相关文章

  • 无料钟炉顶液压传动优化方案 无料钟炉顶液压传动优化方案

    现以某厂2号高炉的液压传动为例，说明无料钟炉顶液压传动系统的概貌。无料钟炉顶液压传动泵站系统如图7-13所示。液压泵长期运转，一台工作，一台备用。当主油路的压力达9.5MPa时，控制溢流阀的电磁阀4接通，使液压泵在卸荷状态下运转。当压力达到10.5MPa或下降到6MPa时，液压泵就自动停泵并发出信号，过高的压力说明控制电磁阀和溢流阀失灵，过低的压力说明管路破裂大量漏油。......

    2025-09-29

    详细阅读
  • 建筑全生命周期循环系统优化方案 建筑全生命周期循环系统优化方案

    分析建筑全生命周期的物质循环过程，可以研究影响整个循环系统物质流的主要因素。建筑生命周期循环系统，是建筑生命周期内各个阶段与自然界构成的一个大系统。建筑生命周期物质循环系统的平衡程度反映了清洁生产的实施绩效。因此，建筑全生命周期的生态平衡系数，是清洁生产的关键评价指标。......

    2025-09-29

    详细阅读
  • 水库防洪计算：溢洪道无闸门控制的优化方案 水库防洪计算：溢洪道无闸门控制的优化方案

    可见，此类水库防洪限制水位、堰顶高程均由正常蓄水位所决定，故防洪计算的内容，主要是选择溢洪道宽度B，并确定其相应的设计洪水位、校核洪水位和坝顶高程。溢洪道无闸门时，常见情况是下游无防洪要求，其防洪水利计算的步骤如下：拟定比较方案。按总费用最小原则，可得最佳的溢洪道宽度Bp以及相应的坝顶高程与最大下泄量。......

    2025-09-29

    详细阅读
  • 中频无芯感应熔炼炉液压系统优化方案 中频无芯感应熔炼炉液压系统优化方案

    如果需要液压系统终止工作，则可以停泵。4）系统设有安全溢流阀和单向阻尼阀，可以防止液压缸过载和倾炉缸下降时超速，安全可靠。此缸倒置后可减轻因粉尘及飞溅钢花引起缸唇口密封过早磨损，从而可减轻活塞杆拉伤所造成的液压缸渗油。......

    2025-09-29

    详细阅读
  • 全相位滤波理论的发展现状探析 全相位滤波理论的发展现状探析

    王兆华教授首次给出了无窗、单窗和双窗全相位滤波器的结构形式及其频率特性图；其提出的“全相位FFT谱分析”极大地抑制了频谱泄漏，所有这些奠定了全相位滤波的理论基础。至2001年以来，王兆华教授和侯正信教授指导多名研究生不断丰富全相位滤波的理论并挖掘在多个领域的应用。此外，全相位滤波理论也在通信、语音信号处理、信号重构等方面得到了应用。......

    2025-09-29

    详细阅读
  • 无换向器电动机调速系统优化方案 无换向器电动机调速系统优化方案

    由于无换向器电动机本质与普通直流电动机相同，因此其调速系统可以和直流电动机调速系统一样采取转速电流双闭环控制。无换向器电动机调速系统如图6.18所示。无换向器电动机控制一般采用晶闸管器件，成本较低，频率与转速同步，没有失步问题，适用于高电压、大电流、大容量同步电动机调速系统。......

    2025-09-29

    详细阅读
  • 全相位滤波方法及其在信号处理中的应用 全相位滤波方法及其在信号处理中的应用

    针对不同类型的信号，信号处理涉及的内容主要包含滤波、变换、检测、谱分析、估计、压缩、识别等方面。滤波的主要任务是设计特性数字滤波器以得到不同频率成分的信号分量，如高通滤波可得到信号的高频成分，中值滤波则可降低高频分量起到平滑的效果。检测和估计主要是从受噪声干扰的杂波中利用信号的统计特性得到有用信号的过程。压缩是信号处理的一个重要方面，它主要是消除信号自身的相关性从而达到减少数据量的效果。......

    2025-09-29

    详细阅读
  • 衬底解取向优化方案 衬底解取向优化方案

    一般来说，衬底表面的形态决定着生长机制。当表面平面相对于普通晶面发生解取向时，表面由许多台阶组成。利用MOVPE，高温生长促使原子向表面和由台阶构成的位错扩散。图2-12所示的为蓝宝石解取向角θ不同时GaN表面的演化。θ约为0.3°时，表面变得更光滑。隆起物的平均高度为5nm。图2-13 GaN在蓝宝石上生长的AFM图像，解取向角分别为θ=0.15°及θ=0.31°注：隆起物（左图）是因围绕螺旋位错的螺旋生长形成的。......

    2025-09-29

    详细阅读