非溶解性有机物是以胶体或悬浮固体形态存在的高分子有机物，因相对分子量大，不能透过细胞膜，因此不可能为细菌直接利用，它们需在第一阶段被胞外酶分解为小分子有机物。例如纤维素被纤维酶水解为纤维二糖与葡萄糖，淀粉被淀粉酶分解为麦芽糖和葡萄糖，蛋白质被蛋白酶水解为多肽与氨基酸等。水解速度可由以下动力学方程表示。表9-2温度与停留时间对污泥中不同组分的值的影响......
2025-09-29
窗函数法及其对滤波器的影响
【摘要】：图2-73 种截断长度对应的滤波器特性图2-7是M分别取5、10及20时得到的一截止频率为0.25π低通滤波器的幅频特性曲线。矩形窗函数的频谱有较大的旁瓣，正是这些旁瓣在卷积时产生了吉布斯现象。另外，设计滤波器的任务又增加了窗函数的设计。窗函数法是针对时域幅度的控制，对频域期望的特性不能得到有效控制。通过窗函数使滤波器的波纹数得到了减少，但却增加了过渡带宽度。
带限信号的单位冲击响应h（n）的持续时间是-∞～∞，在物理上是无法实现的。对h（n）截断为有限2M+1项后右移M项，可变成因果性序列，即
hM（n）=h（n-M）n=0，1，…，2M （2-12）
用hM（n）近似代替h（n）研究系统特性存在误差，记逼近误差为ε2，则
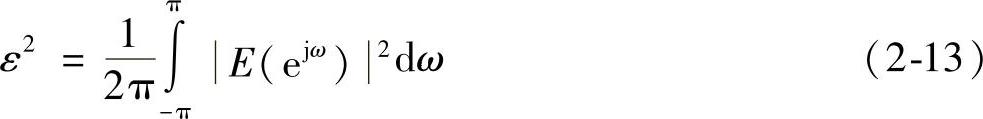
式中，E为hM的幅频特性|HM|和h的幅频特性|H|差值。把HM和H展开成傅里叶级数有
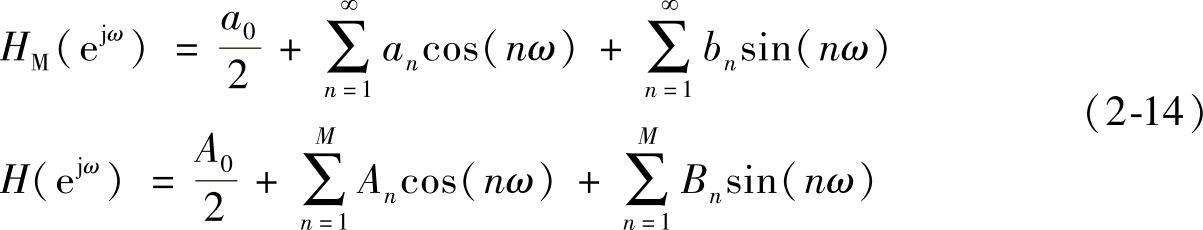
把式（2-14）代入到式（2-13）中并利用三角函数的正交性得到
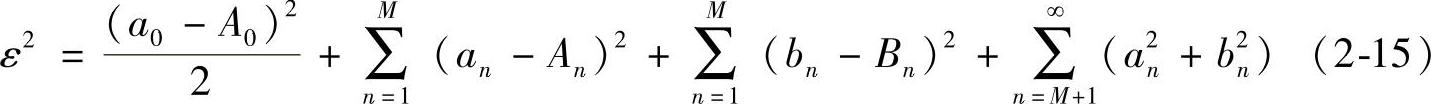
只有当A0=a0，An=an，Bn=bn，n=1，2，…，M时ε2才最小。亦即用HM来近似H的最小误差的条件是HM的单位抽样响应必须是H的傅里叶系数。所以，有限项傅里叶系数是在最小二次方意义上对原信号的最佳逼近，且M取得越大，误差ε2越小。
图2-73 种截断长度对应的滤波器特性
图2-7是M分别取5、10及20时得到的一截止频率为0.25π低通滤波器的幅频特性曲线。当M取不同值时，HM都在不同程度上近似于H。M过小时，通频带过窄且阻带内波纹较大。M增大时，通频带接近0.25π且阻带内波纹减小，但在通带内出现了波纹，随着M的继续增大，这些波纹并不能消失，只是最大的上冲越来越接近间断点，这就是吉布斯现象。
MATLAB实现如下：
(https://www.chuimin.cn)
对hM的自然截断等于对它施加了一个矩形窗口w，在频域则相当于HM与w的频谱W的线性卷积。矩形窗函数的频谱有较大的旁瓣，正是这些旁瓣在卷积时产生了吉布斯现象。为了减小吉布斯现象，可以选取一些旁瓣较小的窗口，如三角窗、汉宁窗等来代替矩形窗。图2-8中给出了M=10时分别加矩形窗和汉宁窗后的幅频特性曲线。
图2-8 加矩形窗和汉宁窗后的幅频特性
MATLAB实现如下：
在MATLAB中窗函数有矩形窗、三角窗、巴特利特窗、汉明窗、汉宁窗、布莱克曼窗、切比雪夫窗和凯泽窗，对应的函数波形和频谱曲线如图2-9所示。
图2-9 8种窗函数的波形和频谱图对比
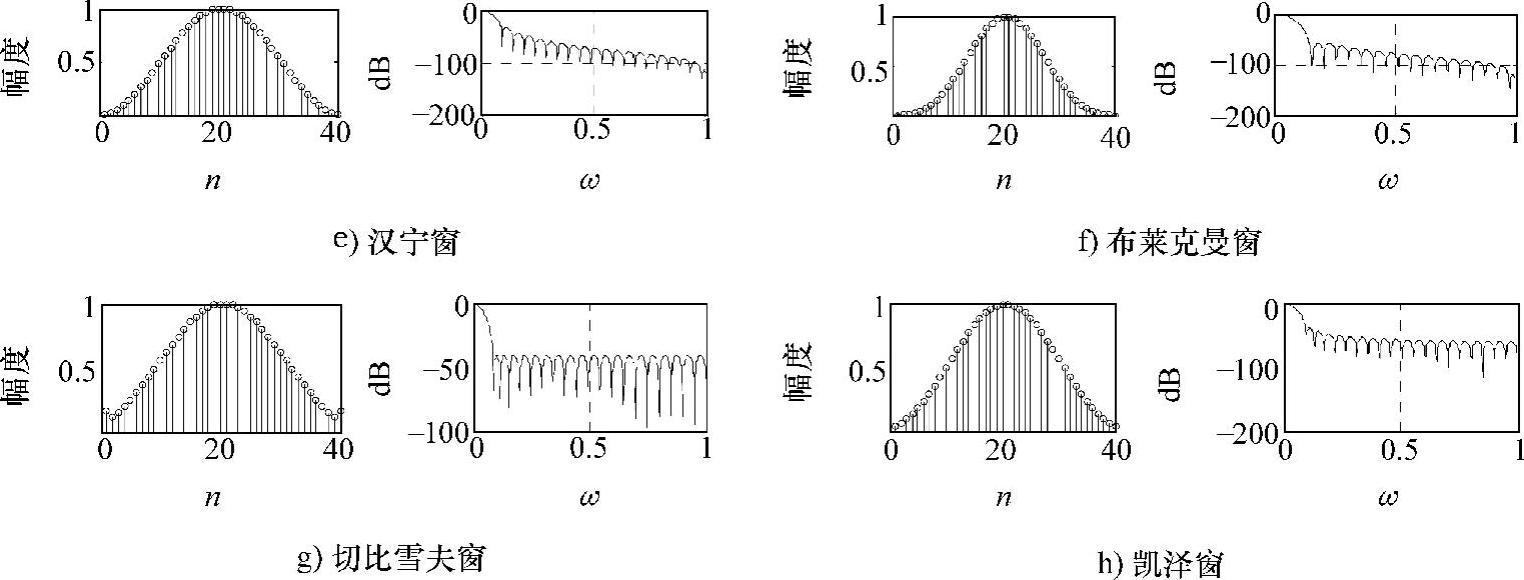
图2-9 8种窗函数的波形和频谱图对比（续）
8种窗函数的MATLAB实现如下：
通过窗函数使滤波器的波纹数得到了减少，但却增加了过渡带宽度。另外，设计滤波器的任务又增加了窗函数的设计。窗函数法是针对时域幅度的控制，对频域期望的特性不能得到有效控制。
相关文章
- 详细阅读
-
稻米直链淀粉的特性及其对大米品质的影响详细阅读
稻米直链淀粉分子与脂肪易形成螺旋状结构，表现出遇热稳定的性质，并能截留脂肪酸和烃类物质。淀粉的吸水膨胀能力，则随着直链淀粉含量的升高逐渐降低，当直链淀粉含量为60%时达最低值。不溶性直链淀粉主要是直链淀粉与脂类及其他物质的复合物，二者的比例不同会影响稻米的品质，而且发现不溶性直链淀粉与大米的蒸煮特性有关。直链淀粉可使淀粉发泡产品的密度下降、硬度增大，而剪切度下降。......
2025-09-29
-
强迫对流及其对低压配电柜温升特性的影响详细阅读
根据上述结果，可以发现进线断路器上接线端子在仿真分析和实验验证中超标严重。本节主要来探究该开关柜在额定电流条件下，出气口安装风扇后，开关柜的温升特性。此外，为了更好地降低开关柜温升，将进气口和出气口也扩大了一定比例，见表5-6。风扇流速对进线断路器上接线端子温升的影响如图5-30所示。......
2025-09-29
-
电子风力对电迁移现象的影响详细阅读
是假想电荷数，它所表示的是电子与扩散原子之间动量交换的力的等效效果；eE是电子风力，在良导体中通常它是直接力的十倍左右，在金属的电迁移现象中电子风力的作用要远大于直接力。所以，在电迁移现象中，被增强的原子扩散通量方向通常与电子漂移通量方向一致。换句话说，它将会体验到更大的电子散射作用，以及更大的电子风产生的力的作用，从而将其推向下一个平衡位置，即该原子扩散前空位所在位置。......
2025-09-29
-
允许的电压偏移及其影响详细阅读
电压过大地偏离额定值将对用户产生不良的影响。电压偏高时，照明设备的寿命将要缩短。电压偏移过大，除了影响用户的正常工作外，对电力系统本身也有不利影响。目前，我国规定的在正常运行情况下供电电压的允许偏移如下：35kV及以上供电电压正、负偏移的绝对值之和不超过额定电压的10%；10kV及以下三相供电电压允许偏移为额定电压的±7%；220V单相供电电压允许的偏移为额定电压的＋7%和－10%。......
2025-09-29
- 详细阅读
-
工艺力对产品的影响详细阅读
图4.11三指机械手中工件的抛光工艺在图4.12所示的情况下，如果要从货架或底座上取下工件，则不能始终保证搬运系统定位的足够精度。图4.12从货架上取走工件补偿装置安装在机械手和搬运系统之间。图4.16FTC运动的可能性图4.17FTC传感器模块在装配阀体中的应用柔性和刚性传感器是有区别的。图4.18FTC传感器的剖视图图4.19FTC位置传感器测量原理这些传感器有不同的尺寸。......
2025-09-29
-
淀粉的溶解特性及其影响因素详细阅读
淀粉的溶解特性常用吸水率、溶解度、溶解率和膨胀度（膨润力）来表示。膨胀度为湿淀粉重量与起始淀粉重量的比值。稻米淀粉的水吸收率和溶解度在60～80℃缓缓上升，在90～95℃急剧上升。在60～80℃热水中，天然淀粉粒由于氢键的断裂，晶体结构被破坏，水分子通过氢键连接到直链淀粉和支链淀粉暴露的羟基基团上，这会引起膨胀和溶解。纯直链淀粉与支链淀粉在水中分散性能不同，可从它们的分子结构与性质的关系来解释。......
2025-09-29
相关推荐