实用的FIR数字滤波器设计方法

2025-09-29 理论教育版权反馈

【摘要】：数字滤波器的设计是数字信号处理的主要内容之一。数字滤波器按单位脉冲响应长度可分成无限脉冲响应滤波器和有限脉冲响应滤波器两类，分别称为IIR滤波器和FIR滤波器；按照滤波器的实现方法可以分成递归滤波器和非递归滤波器两类。在实际的信号与信息处理中，如图像信号处理、数据传输等对线性相位要求较高，并从设计灵活度和控制性角度来考虑，本书主要研究FIR滤波器的设计与应用。

数字滤波器（DF）的设计是数字信号处理的主要内容之一。数字滤波器与模拟滤波器一样，从频率响应分类可以划分为低通、高通、带通和带阻等滤波器，当然还有其他一些按照具体技术要求提出的滤波器。我们知道，序列的傅里叶变换具有以2π为周期的周期性，数字滤波器的特性也具有这一周期性，各种滤波器的幅度特性如图2-1所示。由图中可见，低通通带处于0或2π整数倍频率附近，高通通带处于π的奇数倍频率附近。

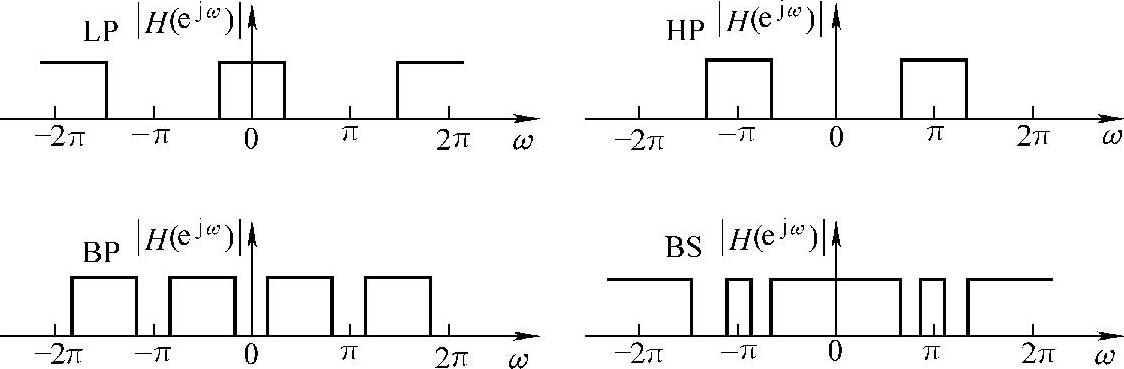
图2-1 各种DF的幅度特性示意图

滤波器的设计任务就是根据预先规定的技术指标，找到系统传输特性H，使滤波器的性能满足技术指标。滤波器的技术指标可以在频域也可以在时域给出，但通常是在频域给出。图2-1所示的是一些理想非因果滤波器的幅频特性。实际设计中只能是尽量逼近它，只要满足指定的指标就可以了。一个实际滤波器的幅频特性在通带内允许有一定的波动，阻带衰减大于给定的衰减，且在通带、阻带之间允许有一定宽度的过渡带。图2-2示出了一个低通的幅频特性。

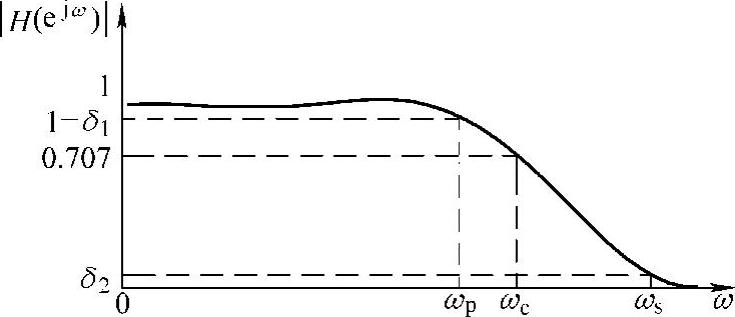
图2-2 低通数字滤波器的幅频特性(https://www.chuimin.cn)

通带范围是0≤ω≤ω_p，在通带内要求1-δ₁≤|H（e^jω）|≤1，ω_p称为通带上限频率或滤波器的截止频率。频率范围ω_s≤ω≤π称为阻带，在阻带内要求|H（e^jω）|≤δ₂，ω_s称为阻带下限频率。频率在ω_p和ω_s之间称为过渡带，一般要求在过渡带幅频特性单调下降。通带衰减（波动）和阻带衰减（波动）通常用分贝（dB）表示。

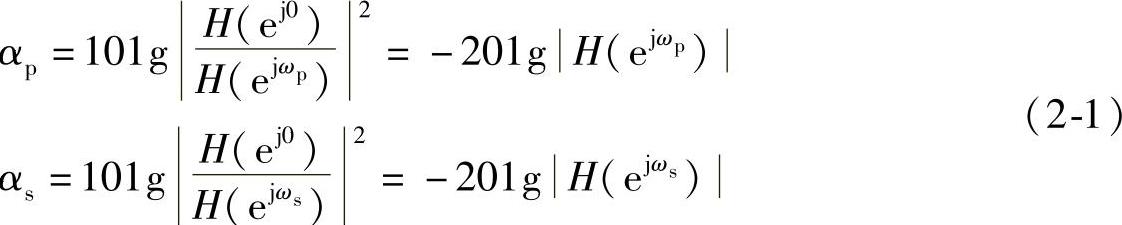
式中，α_p和α_s分别称为通带最大衰减和阻带最小衰减。如果ω_c=3dB，则称为3dB截止频率，对应的带宽称为3dB带宽。

数字滤波器按单位脉冲响应长度可分成无限脉冲响应滤波器和有限脉冲响应滤波器两类，分别称为IIR滤波器和FIR滤波器；按照滤波器的实现方法可以分成递归滤波器和非递归滤波器两类。在实际的信号与信息处理中，如图像信号处理、数据传输等对线性相位要求较高，并从设计灵活度和控制性角度来考虑，本书主要研究FIR滤波器的设计与应用。

实用的FIR数字滤波器设计方法

相关推荐