在生长后的冷却期间，由于衬底和GaN的CTE存在差别，将形成很大的应力。对于Al2O3，它的CTE要高一些，热应力是压缩性的，在室温下使晶片形成凸起翘曲。图2-15 晶片曲率是GaN薄膜厚度的线性函数根据曲线的斜率，可以计算出热应力。应力为临界值时，衬底中会出现裂缝并在GaN层中传播。已经在厚度大于20μm的GaN层中观察到这种现象[HIR 93]。......
2025-09-29
如何避免截断引入误差？
【摘要】：但有一个必须正视的问题，就是数字信号是通过对原始模拟信号按照奈奎斯特取样定理而得到，在实际处理时由于受到物理设备条件的限制，往往是对有限长度的数字信号进行分段处理，从而引入截断误差。很明显，对于非周期信号局部的特性与整体特性是有差异的，如白噪声信号在截取后的均值、方差等各统计特性都会发生变化，而通过分析截断信号的特性去理解原始信号就会引入误差。图1-2 频率偏离带来的幅频偏差图1-2 频率偏离带来的幅频偏差
不管是信号处理的哪种应用，都是对输入信号进行某种特定的处理后得到期望的结果。从这个角度来理解，数字信号处理的过程就是一种滤波的过程，不同的应用只是采用滤波的方法不同而已。但有一个必须正视的问题，就是数字信号是通过对原始模拟信号按照奈奎斯特取样定理而得到，在实际处理时由于受到物理设备条件的限制，往往是对有限长度的数字信号进行分段处理，从而引入截断误差。如理想矩形波采用有限阶数的正弦函数表示时会出现吉布斯振荡，物理可实现的有限长度滤波器在过渡带两边也会出现振荡现象。很明显，对于非周期信号局部的特性与整体特性是有差异的，如白噪声信号在截取后的均值、方差等各统计特性都会发生变化，而通过分析截断信号的特性去理解原始信号就会引入误差。对于周期信号也是如此，若取样频率不是信号频率的整数两倍以上，则取样信号的特性将发生改变。我们通过下面这个例子证明：分别以fs1=128Hz和fs2=135Hz的采样频率对单频正弦波x（t）=sin（2πf0t）进行采样后得到的序列为x1（n）=sin（2πf0/fs1n）和x2（n）=sin（2πf0/fs2n）。假设f0=16Hz，FFT变换后的幅频特性如图1-1所示。
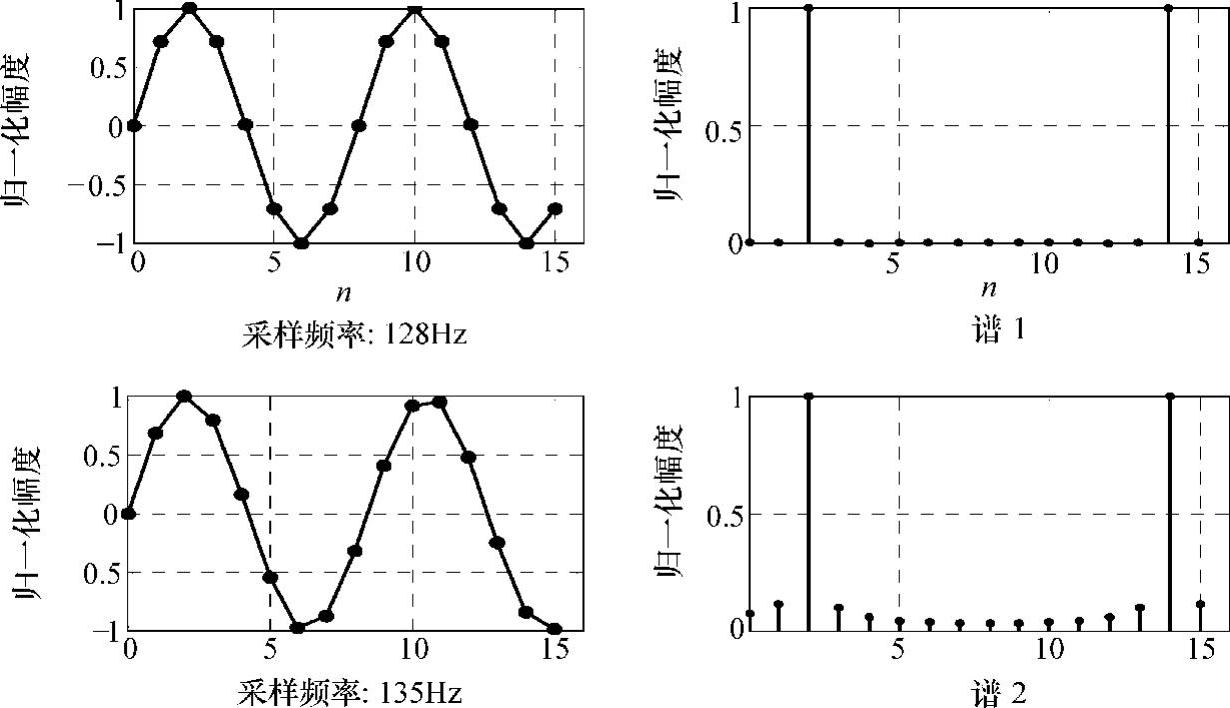
图1-1 两种采样频率下频谱对比
由于采样频率135Hz不是16Hz整数倍，频谱出现扩散且扩散程度与采样频率偏离程度有关。图1-2给出了扩散程度对于采样频率与128Hz的偏离度的规律。在整倍频和半整倍频之间的采样会带来幅频偏差，且会随着频率偏移的增大而增大。(https://www.chuimin.cn)
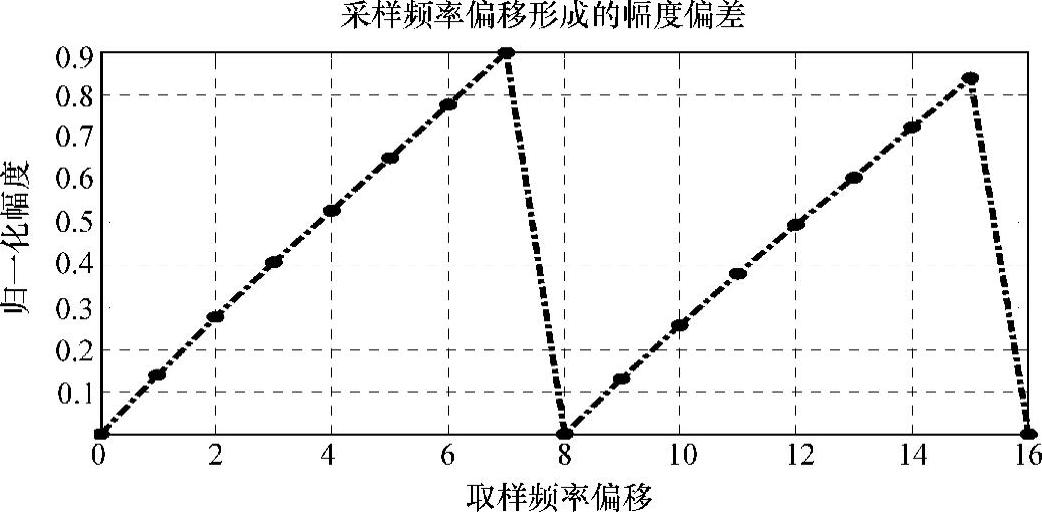
图1-2 频率偏离带来的幅频偏差
相关文章
- 详细阅读
-
如何优化曲面设计，避免加工困难？详细阅读
②用于创建曲面的边界曲线要保持光滑连续，避免产生尖角、交叉和重叠；另外，在创建曲面时，需要对运用的曲线进行曲率分析，使曲率半径尽可能大，否则会因形状过于复杂而导致加工困难。③避免创建非参数化曲面特征。⑥曲面特征之间的圆角过渡应尽量在实体上进行操作。⑦曲面的曲率半径和内圆角半径不能太小，要略大于标准刀具的半径，否则容易造成加工困难。......
2025-09-29
-
剩余电荷触电：如何避免安全事故？详细阅读
图1-5感应电压触电（三）剩余电荷触电检修人员在检修或用绝缘电阻表摇测停电后的并联电容器、电力电缆线路、电力变压器及大容量电动机等设备时，由于检修、摇测前或摇测后没有对其充分放电，这些设备的导体上留有一定数量的剩余电荷。另外，并联电容器退出运行后未进行人工放电，它的极板上也将带有大量的剩余电荷。此时如触及这些带有电荷的设备，大量电荷将通过人体放电，造成触电事故，这种触电称为剩余电荷触电。......
2025-09-29
-
如何正确润滑设备？—优化润滑技术，避免设备故详细阅读
其中80％的零件损坏是由于异常磨损引起的；60％的设备故障由于不良润滑引起；54％的轴承失效是由于不良润滑引起的。2)高温固体润滑。②润滑油是设备润滑应用得最广泛的润滑剂。高温下工作的机械设备，如空气压缩机、内燃机、气锤等要求润滑油具有较高的闪点。贮存和使用中的润滑油酸值增高，表示润滑油的氧化变质。如空气压缩机、内燃机等设备使用的润滑油，残炭指标应低。......
2025-09-29
-
如何避免涂料变稠？分享几点经验详细阅读
4）聚氨酯类固化剂与空气中的潮气发生反应。6）涂料贮存时间过久、温度过高，会造成涂料中树脂的进一步聚合而析出，因此也会引起变稠。3）经常检查涂料包装桶是否密封，防止聚氨酯固化剂与空气接触而发生反应，防止溶剂挥发。贮存时需防止温度过高或过低，控制温度在15～25℃之间。......
2025-09-29
-
如何利用热敏电阻避免继电器触点竞争？详细阅读
但如果利用负温度系数热敏电阻的延时开关特性，便能方便而有效地防止继电器触点竞争。接触器KM、继电器KA2同时通电。触点5使KA2自锁；触点4使继电器KA1失电，使其触点1、2、3复位。图2-14CTR防止触点竞争线路例一现在在KA2支路中串入Rt后，情况又是怎样呢？该线路为一组风机定时顺序起动线路，Rt1、Rt2是CTR热敏电阻。......
2025-09-29
-
计算电能计量装置综合误差详细阅读
对于Ⅰ、Ⅱ、Ⅲ类电能计量装置，应按整个装置的综合误差进行考核。表26图13.1.11 “查看分型结果”对话框图13.1.12 创建的型腔注对于安装1.0级有功电能表和0.5级互感器的Ⅰ类电能计量装置，其综合误差应符合Ⅱ类电能计量装置的综合误差的要求。电能计量装置的综合误差，在电能表的经常运行负载下，不应超过表26的规定。......
2025-09-29
-
如何避免芯片焊点时变熔化的倒装问题？详细阅读
对于某些共晶锡银铜倒装芯片焊点，当外加的电流密度高于5×104 A/cm2，并且试验温度在100℃左右时，就会发生熔化。然而，我们观测到在倒装芯片焊点中，由电迁移引起的熔化现象是在一定时间内才完成的。为何在倒装芯片焊料凸点内所产生的焦耳热如此之大，以及熔化为何需要时间都需要合理的解释。如9.2.4.节中所讨论的，当电流密度很高时，电迁移会在铝中造成损伤。......
2025-09-29
相关推荐