比较CB3和CB1的计算结果,将静导电杆的形状从水平U型改为平板型,电动斥力有所减小,说明水平U型通过改变电流的方向,有利于加强触头区域的磁场及相应的电动斥力,这一点也和图6-20的结果相一致。对CB1和CB2来说,FH分别为40.33N和38.45N,同表6-4的结果相比,有一定的差别,这主要是由于导电回路产生的磁场对动触头上电动斥力的影响引起的。表6-4 5个模型在10kA电流时的电动斥力计算结果......
2025-09-29
利用建立的准二维数学模型以及设计的水沙条件与河床边界条件进行计算。结果显示小浪底水库运用初期库区为三角洲淤积,其淤积机理是挟沙水流运行至水库回水末端以下处于超饱和状态,较粗泥沙很快落淤而形成三角洲淤积体。水库调控流量时的蓄水作用及每年10月~翌年6月份的调节期使三角洲洲面不断淤积抬升。位于三角洲顶点以下的前坡段水深陡增,流速骤减,水流挟沙力急剧下降,大量泥沙落淤,使三角洲不断向下游推进。图13-23为历年汛后库区河槽纵剖面,可以看出这种变化过程。
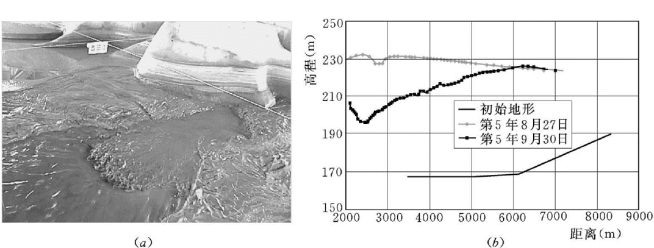
图13-22 降水冲刷试验结果
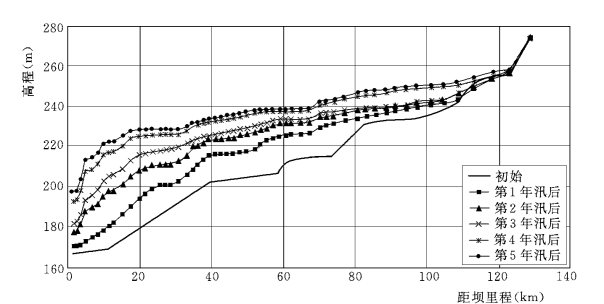
图13-23 河槽纵剖面
水库运用初期大多时段为异重流排沙,异重流潜入位置一般位于库区淤积三角洲前坡段,随着水库淤积三角洲不断向坝前推进,异重流潜入位置不断下移。图13-24显示了异重流潜入点随水库运用时间变化而变化的过程。可以看出随着水库运用时间的延长,异重流潜入点的变化趋势是不断下移的,同时亦会随坝前水位的升降及入库流量的大小而发生变化。在水库投入运用初期,异重流潜入位置一般位于距坝60~70km 处,第1年7月中旬以后,异重流潜入位置下移至距坝60km 以下,至第5年下移至距坝10~20km 处。第1年~第5年的6~10月份,出现异重流排沙的天数为611天,占该时段天数的80%。其中7月1日~9月30日异重流排沙几率为95%。
表13-7为小浪底水库数学模型计算出的水库运用初期1~5年内库区不同粒径组泥沙及全沙淤积量,显示前5年库区总淤积量为37.0亿t,平均排沙比约17.7%,其中距坝67km 以下分别淤积4.54亿t及32.46亿t,即淤积泥沙绝大部分分布在库区下段。库区D<0.025mm、D=0.025~0.05mm 及D>0.05mm 的泥沙淤积量占总淤积量的比值分别为46.5%、27.3%、26.2%。总的看来d<0.025mm 的细颗粒泥沙的排沙比均大于较粗泥沙的排沙比。(https://www.chuimin.cn)
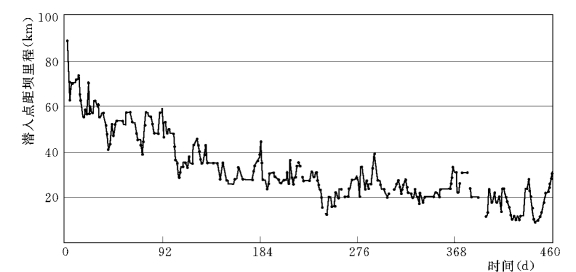
图13-24 异重流潜入位置变化过程
表13-7 水库运用初期1~5年库区输沙计算结果
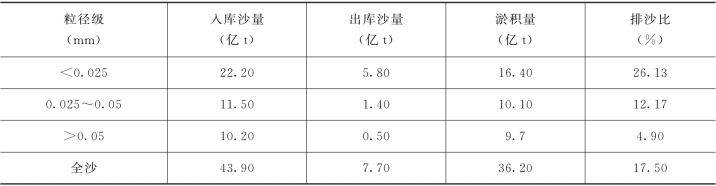
在相同的水沙条件及边界条件下进行的小浪底库区实体模型试验结果表明,距坝67km 以下库段总淤积量为29.44 亿m3,若淤积物干容重γ0=1.15t/m3,则淤积量为33.8亿t。两者较为接近。图13-25为两者第1年及第5年汛后河床纵剖面图,可以看出淤积形态也较为接近。
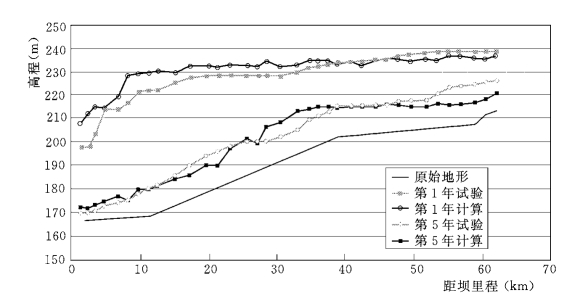
图13-25 干流淤积纵剖面计算与试验结果对比
相关文章

比较CB3和CB1的计算结果,将静导电杆的形状从水平U型改为平板型,电动斥力有所减小,说明水平U型通过改变电流的方向,有利于加强触头区域的磁场及相应的电动斥力,这一点也和图6-20的结果相一致。对CB1和CB2来说,FH分别为40.33N和38.45N,同表6-4的结果相比,有一定的差别,这主要是由于导电回路产生的磁场对动触头上电动斥力的影响引起的。表6-4 5个模型在10kA电流时的电动斥力计算结果......
2025-09-29

图12-9流域水沙资源优化配置数学模型框图流域水沙资源优化配置的方法采用多目标规划法,其优化配置模型目前宜采用多目标线性规划数学模型。根据流域水沙资源多目标优化配置原理,联合水资源优化配置,以泥沙资源优化配置为重点,结合专家调查和层次分析数学方法,构造综合目标函数,深入研究水沙资源优化配置的各种方式,确定配置约束条件,建立流域水沙资源多目标优化配置数学模型。......
2025-09-29

图12-15洛口—利津河段均衡稳定断面计算12.9.1.2恢复和维持稳定中水河槽的措施及冲淤调整量恢复和维持黄河下游稳定中水河槽的措施主要包括改善小浪底水库运用和下游河道的整治及疏浚。......
2025-09-29

10.4.2.4沉降系数确定图10-16航道疏浚深度与悬沙沉降系数的关系在悬沙不平衡输沙方程和河床变形方程式中,沉降系数α 对河床冲淤强度有较大影响。......
2025-09-29

简单的尼迈亚模型是一种经验公式类型的电弧数学模型,按图8-1所示,断路器开断过程可分成4个过程,它们是1)瞬动电磁铁动作过程;2)电弧停滞过程;3)电弧运动过程;4)电弧进入电弧栅片熄灭过程。经过停滞阶段后,电弧开始运动,迅速从动触头转移到导弧板,并在磁场力的作用下向栅片运动,计算这一阶段的电弧电压Uarc需要建立电弧动态数字模型,这里介绍尼迈亚模型,它由L.Niemeyer博士于1984年提出[1]。......
2025-09-29

图3.1a所示模型中转子和定子的频率不同,转子和定子回路之间由互感联系,不便于计算,一般通过频率折算、绕组折算和磁通折算得到异步电动机的等效模型,如图3.1b所示。电动机定子互感电动势Esm和转子互感电动势Erm的关系为Eg=Esm=keErm (3.6)其中式中,N1、N2分别为定子和转子一相绕组匝数;kW1、kW2分别为定子和转子的绕组系数。......
2025-09-29
相关推荐