流域水沙资源多目标优化配置数学模型简述

2023-06-23 理论教育版权反馈

【摘要】：对于复杂的流域水沙资源多目标优化配置问题，结合层次结构分析，

12.8.3.1　流域水沙资源多目标优化配置原理

流域水沙资源优化配置原理是指对流域系统从产水产沙经过水土保持减水减沙后进入河流的水沙资源总量，进一步通过水库群的联合拦水拦沙和调水调沙运用改善河道水沙条件，通过合理分配水库调节水量、工农业用水量、输沙用水量和生态用水量等方式优化配置水资源。结合河道的综合治理，改善河道输水输沙能力和维持河道稳定，通过水土保持(植物固沙和坝地减沙)、水库调控(水库拦沙和放淤利用)、引沙淤灌 (引水引沙和机淤固堤)、河道滞沙(维持河槽和滩区淤沙)、输沙入海(河口造陆和深海输沙)等多种手段方式优化配置和合理利用泥沙资源，创造最大的社会、经济和生态多目标水沙资源利用综合效益。在数学上表述为在各种水沙资源配置约束条件下，使流域水沙资源优化配置的综合目标函数最大或拟最大，其表达式为

综合目标函数

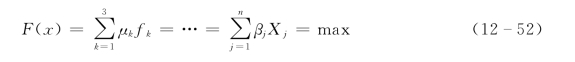
pagenumber_ebook=570,pagenumber_book=554

配置约束条件

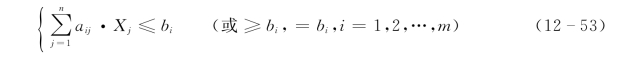
pagenumber_ebook=570,pagenumber_book=554

式中:F(x)为综合目标函数，其表达式通过多目标规划层次分析数学方法构造;fk为各子目标函数;μk为各子目标函数的权重系数;Xj为泥沙配置方式变量;βj为综合目标函数的权重系数;n泥沙配置方式变量个数;bi为各约束条件的水沙资源约束量;aij为各约束条件的水沙系数;m 为约束条件个数。

流域水沙资源多目标优化配置层次分析如表12-4所示，配置层次主要包括总目标层、子目标层、效益指标层和配置方式层。对于配置方式层，水资源配置方式主要包括水土保持减水量、水库调节水量、放淤利用耗水量、工农业生活引水量、汛期输沙用水量和非汛期生态用水量，泥沙资源配置手段主要包括水土保持、水库调控、引沙淤灌、河道滞沙和输沙入海等5种手段，其中水土保持手段包括植物固沙和坝地减沙两种配置方式，水库调控手段包括水库拦沙和放淤利用两种配置方式，引沙淤灌手段包括引水引沙和机淤固堤两种配置方式，河道滞沙手段包括维持河槽和滩区淤沙两种配置方式，输沙入海手段包括河口造陆和深海输沙两种配置方式。

需要指出的是，这里提出的流域水沙资源优化配置方法是一般性的，对于不同河流及同一河流的不同区段，水沙资源优化配置的具体方式可以有一定的差别，例如，对于泥沙相对较少的河流，为了控制河道私采乱挖对河道稳定带来不利影响，河道采砂可以作为独立的泥沙资源优化配置方式;对于河流的中上游区段，没有河口造陆和深海输沙配置方式，而变为区段出口的下游水沙量;对于河流的下游区段，通常没有水土保持配置方式。

表12-4　流域水沙资源多目标优化配置层次分析表

pagenumber_ebook=571,pagenumber_book=555

12.8.3.2　流域水沙资源多目标优化配置数学模型

流域水沙资源多目标优化配置数学模型采用多目标线性规划方法，数学模型方程由综合目标函数式(12-52)和配置约束条件式(12-53)两部分构成，求解模型得到一个最优或拟最优的规划方案。

1.综合目标函数

由于综合目标函数决定水沙资源优化配置的效果评价，甚至影响水沙资源配置方案，因此，建议结合层次数学分析和专家调查统计两种方法构造水沙资源优化配置的综合目标函数。通过发放水沙资源多目标优化配置层次分析重要性排序评价专家调查表，结合专家调查统计结果，利用层次数学分析方法(吴祈宗，2003)，对各配置层次的组成元素进行两两比较，由9标度法得到判断矩阵，求判断矩阵最大特征值对应的归一化权重系数特征向量，通过逐层的矩阵运算方法求各决策变量的权重系数βj，构造综合目标函数

构造综合目标函数的具体步骤如下:

(1)建立系统的层次分析结构。分析系统中各个因素的关系，结合水资源优化配置，以泥沙资源优化配置为重点，建立系统的流域水沙资源多目标优化配置层次分析结构。对于复杂的流域水沙资源多目标优化配置问题，结合层次结构分析，建立并发放水沙资源多目标优化配置层次分析重要性排序评价专家调查表 (如表12-5 所示)，统计专家调查结果。

(2)构造各层次的两两比较判断矩阵。结合专家调查统计结果，对同一层次的各元素关于上一层次中某一准则的重要性进行两两比较，由9标度法构造两两比较判断矩阵A=(aij)n×n，Satty建议用1～9及其倒数做为标度来确定aij的值(吴祈宗，2003)，1～9比例标度的含义为配置措施或变量Xi比Xj重要的程度(见表12-6)。

表12-5　流域水沙资源多目标优化配置层次分析重要性排序评价专家调查表例

pagenumber_ebook=572,pagenumber_book=556

表12-6　层次分析重要性程度9标度法取值表

pagenumber_ebook=572,pagenumber_book=556

(3)判断矩阵最大特征值对应的特征向量确定排序权重系数向量。用两两比较判断矩阵为A= (aij)n×n计算排序权重系数向量:

1)计算矩阵A 的最大特征值λmax及相应的归一化 (标准化)特征向量μ，可采用MATLAB矩阵计算通用软件计算。

2)确定判断矩阵一致性指标C.I.(Consistency Index):

pagenumber_ebook=572,pagenumber_book=556

3)查表12-7求相应的平均随机一致性指标R.I. (Ratio Index):

表12-7　平均随机一致性指标表

pagenumber_ebook=572,pagenumber_book=556

4)计算一致性比率C.R. (Consistency Ratio):

5)判断矩阵一致性。当C.R.＜0.1，认为判断矩阵A 的一致性可接受;否则，若C.R.≥0.1，应考虑修正判断矩阵A。

(4)计算各层元素对系统总目标的合成权重。计算矩阵A 的最大特征值λmax及相应的归一化(标准化)特征向量μ，从而构造水沙资源优化配置综合目标函数式(12-52)。

2.配置约束条件

流域水沙资源多目标优化配置方案受配置约束条件控制。这些约束条件既可以是线性方程，也可以是非线性方程。对于流域面上的水沙资源总量优化配置，本模型采用线性约束方程式(12-53)，这些约束条件主要包括:

1)水土保持能力约束。水土保持包括植物固沙和坝地减沙两种配置方式。统计水土保持减水减沙资料，建立减沙与减水关系，分析确定水土保持能力约束。

2)水库拦沙能力约束。研究水库运用方案，特别是上中游多个水库联合调度运用方案，通过水库多年调节平衡，拦粗排细、蓄清排浑和敞泄排沙等措施合理拦沙，尽量延长拦沙库容使用寿命，从水沙资源优化配置的角度确定拦沙库容使用年限，确定水库拦沙能力约束。

3)放淤利用能力约束。放淤利用包括人工渠引高含沙水流放淤、机械泵抽高含沙水流放淤和水库清淤高含沙水流管渠输送放淤等措施，通常通过人工渠引高含沙水流自流放淤措施进行淤滩，通过机械泵抽高含沙水流放淤措施进行固堤，通过水库清淤高含沙水流管渠输送放淤措施进行恢复库容。对于通过水库清淤高含沙水流向河道大堤以外放淤利用泥沙资源，泥沙放淤利用主要受放淤区和管渠输送系统制约，因此，需要深入研究放淤利用泥沙的方案，确定泥沙放淤利用能力约束。

4)引水引沙能力约束。由于工农业和生活用水需要必须引水，引水会携带出一部分泥沙，过量引水不利于河道输水输沙，甚至导致河道功能性断流，危及河流健康生命，因此，必须合理确定引水量及引水引沙能力约束。多沙河流引水引沙能力是比较大的，应特别重视灌区泥沙资源的综合利用，依据规划引水分配方案，通常采用河段进出站平均含沙量的70%计算引沙量及单位引沙用水量，建立引水引沙能力约束。

5)机淤固堤能力约束。机淤固堤是泥沙资源利用的重要措施，机淤固堤主要依靠人工机械措施，包括挖河固堤和疏浚高含沙水流淤临淤背，机淤固堤规划应与标准化大堤建设相结合，计算各河段大堤淤临淤背的泥沙可容量，机淤固堤能力主要受经济投入的约束，因此，要参考既有的机淤固堤水平，确定机淤固堤能力约束。

6)维持河槽稳定约束。目前河流普遍出现河槽淤积萎缩的不利趋势，要深入研究河道输水输沙和河床演变稳定的规律，结合河道综合治理，通过河床演变均衡稳定数学模型或河道水沙数学模型计算，确定维持河槽要求泥沙冲淤调整量约束。

7)滩区淤沙能力约束。对于有宽阔滩地的河流，应结合滩区的综合治理，从水沙资源优化配置和利用的角度，提出可行合理的综合治理方案，计算滩区的面积和容积，结合滩区历史实测滞纳泥沙的能力分析，确定滩区淤沙能力约束。

8)维持河口稳定约束。河口三角洲的稳定受径流来水来沙、风浪侵蚀和潮汐海流输沙共同影响，水沙资源优化配置要达到维持河口三角洲稳定和限制河口延伸的目标，从水沙资源优化配置和利用的角度，提出可行合理的河口综合治理方案，根据实测资料分析计算河口海洋动力侵蚀的年沙量和河口海域的容沙体积，确定维持河口三角洲稳定约束。

9)维持河流健康的水资源约束。水沙资源优化配置是在一定水资源总量条件下进行的优化配置，因此要统计不同历史阶段流域的径流产水总量经过上中游的水土保持、水库拦蓄和工农业引水等减水后进入下游的径流水资源总量，预测未来的水资源条件，提出水库合理调节利用水资源的方案，合理分配水库调节水量、放淤利用等耗水量、工农业生活引水量、汛期输沙用水量和非汛期生态用水量，确定维持河流健康的水资源约束。

10)泥沙资源总量约束。水沙资源优化配置也是在一定泥沙资源总量条件下进行的优化配置，因此，要统计不同历史阶段流域的径流产水总量经过上中游的水土保持、水库拦沙、引水引沙和河道冲淤等减沙后进入下游的泥沙资源总量，预测未来的泥沙资源条件，从泥沙资源总量配置计算的角度，可以得到泥沙资源总量约束。

综上所述，通过合理分配水库调节水量、放淤利用等耗水量、工农业生活引水量、汛期输沙用水量和非汛期生态用水量等配置方式优化配置水资源，通过水土保持、水库拦沙、放淤利用、引水引沙、机淤固堤、维持河槽、滩区淤沙、河口造陆和深海输沙等配置方式优化配置泥沙资源。通过层次分析和专家调查方法对配置层次进行重要性评价，构造水沙资源优化配置综合目标函数，并对各配置方式和措施进行分析，确定各配置约束条件，建立水沙资源多目标优化配置数学模型。

12.8.3.3　流域水沙资源多目标优化配置数学模型求解

流域水沙资源多目标优化配置数学模型方程式(12-52)和式(12-53)可采用线性规划单纯形法求解(吴祈宗，2003;何光渝，2002)。先引入松弛变量，把流域水沙资源多目标优化配置数学模型方程表达为线性规划标准等式形式，再采用单纯形法求解，线性规划单纯形法的基本思路是沿边界域的转轴运算。

1.线性规划标准形式

引入松弛变量，把流域水沙资源多目标优化配置线性规划数学模型方程式 (12-52)和式(12-53)表达为线性规划标准等式形式。

综合目标函数

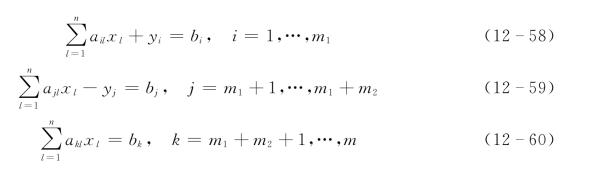
pagenumber_ebook=574,pagenumber_book=558