河床演变的均衡稳定数学模型优化

2023-06-23 理论教育版权反馈

【摘要】：河床演变均衡稳定数学模型由目标函数和约束条件及计算条件组成，分述如下。

根据河床演变均衡稳定原理，冲积河流河床演变达到均衡稳定过程符合河流最小可用能耗率原理，利用该原理的表达式(12-29)封闭河床演变方程组，确定河床演变均衡稳定的目标函数和相应的约束条件及计算条件，即建立河床演变均衡稳定数学模型。模型计算流程见图12-10。河床演变均衡稳定数学模型由目标函数和约束条件及计算条件组成，分述如下。

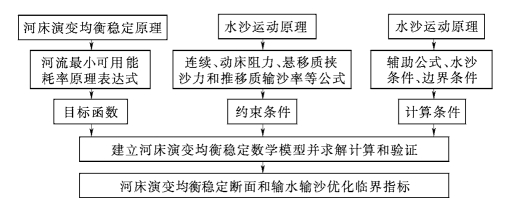
pagenumber_ebook=567,pagenumber_book=551

图12-10　河床演变均衡稳定数学模型计算流程

12.8.2.1　目标函数

在河流最小可用能耗率原理的表达式(12-29)中，用于维持悬移质悬浮作有用功的功率可分解为冲泻质和床沙质的悬浮功率，能坡Je采用水面比降J，通常Je≪tgφ，可得到河床演变均衡稳定数学模型的目标函数

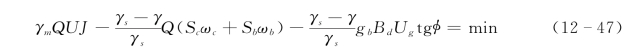
pagenumber_ebook=567,pagenumber_book=551

式中:Sc为冲泻质含沙量;ωc为冲泻质平均沉速;Sb为床沙质含沙量;ωb为床沙质平均沉速。

12.8.2.2　约束条件

河床演变均衡稳定数学模型的约束条件包括连续公式、动床阻力公式、悬移质挟沙力公式和推移质输沙率公式，经计算综合比较，本模型的动床阻力公式、悬移质挟沙力公式和推移质输沙率公式采用韩其为建立的公式(韩其为，2003)。

1.连续公式

式中:Bb为水面宽;hcp为平均水深。

2.动床阻力公式

式中:db50为床沙中值粒径;k为系数，取k=6.5。

3.床沙质挟沙力公式

式中:Sv为体积比含沙量;ωbcp为床沙质平均沉速;K 为挟沙力系数，取K=0.0001465;β为高含沙修正系数，取β=0.5。

4.沙质推移质输沙率公式

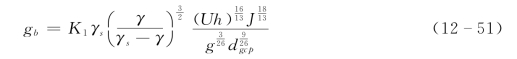
pagenumber_ebook=568,pagenumber_book=552

式中:dgcp为推移质平均粒径;K1为与相对起动流速有关的系数。

12.8.2.3　模型计算条件及求解

模型的计算条件包括辅助公式和水沙河床边界条件。辅助公式有:冲泻质和床沙质及推移质的分界粒径计算、悬移质清水和浑水沉速、推移质运动速度和泥沙水下休止角等公式。水沙河床边界条件有:来水流量 (造床流量)、来水含沙量、来水水温、来沙级配组成和河床级配组成。

模型求解为求在一定约束条件下目标函数的极值，如果约束条件为显函数，可构造拉格朗日极值函数直接求解。本模型中床沙质挟沙力公式为隐函数，因此，模型需采用试算迭代法求解 (陈绪坚，胡春宏，2004)，试算迭代过程如图12-11所示。

试算各河宽对应的可用能耗率，求最小可用能耗率对应的河道均衡稳定断面和水沙条件。根据模型的计算结果，分析河道输水输沙优化的临界指标，确定维持稳定主河槽的措施及冲淤调整量，为水沙资源多目标优化配置模型提供维护主河槽稳定的约束条件。

12.8.2.4　数学模型验证

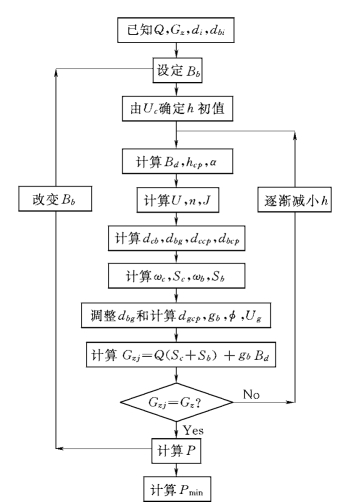
pagenumber_ebook=568,pagenumber_book=552

图12-11　试算迭代过程图

利用黄河下游实测资料对河床演变均衡稳定数学模型进行验证，河床演变均衡稳定理论表明在造床流量条件下河床演变达到均衡稳定，实测资料分析表明，黄河下游的造床过程为非恒定非饱和输沙引起的涨冲落淤过程 (齐璞、孙赞盈等，2003，2004)，洪峰阶段河道趋近于冲淤平衡的均衡稳定状态，由于要求验证资料实测流量接近造床流量，且要求有同步的悬移质和床沙级配等资料，因此，模型验证资料采用黄河下游1982～1988年洪峰流量接近造床流量(5000m3/s)的17测次实测水沙河道资料，验证计算结果如图12-12和图12-13所示。由图可见，随着设定河宽Bb变化，比降J、单位能耗率γUJ 和可用能耗率P 都存在最小值，只有可用能耗率P 的最小值对应的Bb与实测河宽最接近，单位能耗率γUJ 和比降J 最小值对应的Bb皆远小于实测河宽，进一步表明，最小可用能耗率对应的河宽反映了实测河床演变均衡稳定河宽。

pagenumber_ebook=569,pagenumber_book=553

图12-12　孙口站验证算例成果图 (1984年8月8日)(实测Q=5380m3/s，Bb=637m，S=52.8kg/m3)

pagenumber_ebook=569,pagenumber_book=553

图12-13　利津站验证算例成果图 (1988年8月19日)(实测Q=5070m3/s，Bb=505m，S=77.9kg/m3)

河床演变的均衡稳定数学模型优化

相关推荐