12.6.1.1河流水力熵差定义挟沙水流的水力机械能是由水和悬移质所组成的浑水体的势能和动能。......
2023-06-23
河流可用能耗率和统计熵原理
【摘要】：式表明，只有沉速满足的较粗悬移质对降低可用能耗率起作用，自动悬浮理论把式作为划分床沙质和冲泄质的标准。
12.6.3.1 河流最小可用能耗率原理
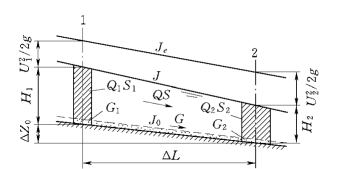
图12-8 河流水力熵差计算示意图
河流和明渠流的差别主要在于河流的河床是可动的，冲积河流的自动调整作用表现为河床和水流自动调整，通过改变河宽、水深、比降和床沙组成使本河段的水流挟沙力与上游的来沙条件趋于相适应，达到输沙相对平衡。冲积河流自动调整作用的最终结果不仅在于满足输沙相对平衡要求，而且还要使体系内部的能量趋向于按照一定的规律进行分配。
与明渠流的总能耗率计算公式 (12-14)推导过程相同 (见图12-8)，将清水比重γ 改为浑水比重γm，即可得出挟沙河流的总能耗率为
总能耗率中用于维持悬移质悬浮作有用功的功率为
式中:S 为悬移质含沙量;ω 为悬移质平均沉速;γs为泥沙比重。
总能耗率中用于维持推移质运动作有用功的功率为
式中:G 为推移质总输沙率，G=gbBd，gb为单宽推移质输沙率，Bd为推移质输沙带宽(可取河底宽);fg为推移质运动与河床的摩阻系数，拜格诺 (Bagnold)通过大量试验分析(钱宁，万兆惠，1983)，得到fg≈tgφ，φ 为推移质水下休止角;J0为河床坡降，对于平原河流，通常J0≪tgφ;Ug为推移质运动速度。式(12-25)可进一步表示为
根据河流水力熵差的定义可直接推求挟沙河流水力熵产生率P 的计算公式
利用开放系统稳定的普适发展判据判定河流的稳定性，则有:
在一定来水来沙条件下，当系统达到动平衡稳定时，则有
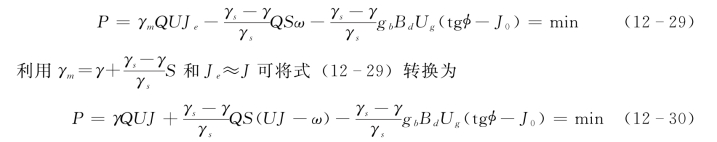
河流最小可用能耗率原理可表达为:在一定来水来沙条件下，河流总是在一定约束条件下努力调整所有可以调整的变量，使挟沙水流的可用机械能损耗率减小，且当河道稳定时为最小，最小值的大小取决于来水来沙和河床边界条件，用式(12-29)表达。式 (12-29)的物理意义是体积为流量Q 的含沙浑水体在向下游流动过程中沿程的可用机械能损耗率最小。对于清水水流，式(12-29)变为明渠流公式 (12-15)。天然河流来水来沙过程是一个非恒定过程，河床演变在造床流量水沙条件下达到均衡稳定，形成相对稳定的河床形态。
当输沙次饱和时，挟沙河流除了通过调整流速和能坡降低可用能耗率，还可通过冲刷河床增大悬移质和推移质输沙率，但输沙率最大不会超过挟沙力。当输沙饱和时，平衡输沙的输沙率等于挟沙力，式(12-29)可变为
式中:Jd为地貌坡降;η为河道弯曲系数。
当输沙超饱和时，则式(12-29)表现为减小γm，河床淤积。河流还可通过调整河宽、水深和增大弯曲系数来降低可用能耗率，其由地貌坡降和河床河岸相对抗冲性决定的不同组合可形成不同的河型。当来水来沙及河床条件变化后，式(12-29)要求河流在新的条件下达到新的最小值，即最小值的大小取决于来水来沙及河床边界条件的约束。因此，式(12-29)在数学上完整地表达了冲积河流的自动调整作用。
式(12-30)表明，只有沉速满足
的较粗悬移质对降低可用能耗率起作用，自动悬浮理论把式(12-32)作为划分床沙质和冲泄质的标准。式(12-29)为了达到最小值，对于一定的流量，床沙质含沙量S 与UJe成正比，与沉速ω 成反比，能反映水流挟沙力的基本公式。单宽推移质输沙率gb与推移质的水下休止角tgφ成反比，和Bagnold等建立的推移质输沙率公式一致。当河床坡降J0大时，推移质输沙能力更强，这也可以反映山区河流的特性。
12.6.3.2 河流统计熵原理
河流能耗的宏观分配体现在各种阻力作用的相对大小，分配关系可在统计熵中体现。根据最大统计熵原理的等概率定理或能量均配定理，可以得到多种广义的河相关系。
1.河宽与水深河相关系
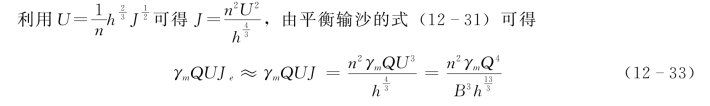
对上式取微分得
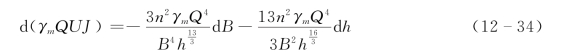
式(12-34)右边两项分别是可用机械能的耗散在河宽变化和水深变化的分配，如果河宽变化和水深变化能自由调整，由能量均配定理，则有:
对上式积分得到
据国内外30个关于河宽与水深河相关系式的指数统计(邓志强，1992)，其平均值为0.6926，此值和9/13=0.6923几乎相同。考虑堤防约束和河岸抗冲性大，河宽与水深经验河相关系式通常采用 B/H=C。
2.流速、含沙量与河床坡降(或河道弯曲系数)河相关系
由式(12-31)可得
式中:Jd为地貌坡降(变化很慢，河床演变研究可认为其不变，它对河型成因起重要作用);η为河道弯曲系数。
式(12-36)说明流速变化、坡降 (或河道弯曲系数)变化和浑水容重变化是同量级的。
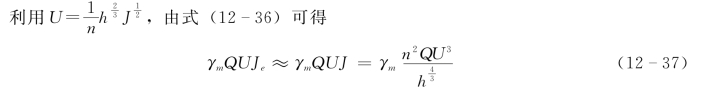
对上式取微分有
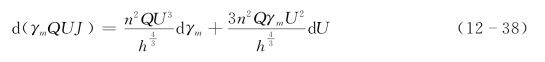
上式右边两项分别是可用机械能的耗散在浑水容重变化和流速变化的分配，冲积河流浑水容重变化和流速变化是能自由调整，由能量均配定理，则有
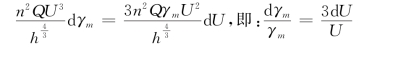
对上式积分得到
式(12-42)表明了含沙量大的河流的水流流速也大，在挟沙力公式中已体现出来，均衡河流取河床坡降J0≈J=Jd/η，式(12-43)和式(12-44)表现了含沙量大的河流的河床坡降也大，而河道弯曲系数小，例如，对于可以自由调整的弯曲河段(黄河下游陶城铺至利津河段，长江荆江河段)，黄河的含沙量比长江大，黄河达到输沙平衡的坡降比长江大，黄河下游的弯曲系数比长江荆江河段小。因此，含沙量高的河流河道整治的弯曲系数应比含沙量低的河流小，也从理论上解释了修建水库拦沙下泄清水冲刷常导致下游河道弯曲率增大，河道易于摆动(钱宁，张仁等，1984)。
从河流最小可用能耗率原理出发，根据最大统计熵原理的等概率定理或能量均配定理，理论上可以得到多种广义的河相关系，但这些河相关系只能反映河床演变的某两个变量之间的关系，而河流最小可用能耗率原理的公式完整地表达了冲积河流自动调整作用原理，反映了河床演变是多个变量之间的综合关系，是河道水沙优化配置的基本原理之一。
有关泥沙研究进展的文章
- 详细阅读
-
明渠流水力熵与统计熵的分析详细阅读
12.6.2.1明渠流水力熵原理对于封闭水体，如一杯晃动的水，当水体达到静平衡时，系统水力熵达到最大，熵产生率最小为零，杯中水的可用机械能最小，水的动能全部通过紊动粘性转化为热能耗散。......
2023-06-23
-
能耗制动技术原理与工作过程详细阅读
能耗制动的技术性能见表4-2。工作过程是，当光耦合器VLC得到信号而导通时，V1导通且饱和，V2随即导通，V3截止，使GTR导通，即有制动电流流经RB。这样多次反复将电能变热能，消耗在制动电阻RB上。当UD超上限值时，比较器的输出为“+”，则光耦合器VLC输出信号电流，再推动驱动电路，实现能耗制动工作状态，当UD低于下限值时，比较器的输出为“-”，则光耦合器VLC无输出电流，这时驱动电路不工作，处于不制动工作状态。......
2023-06-19
-
1978～2010年司法调解率统计及解释详细阅读
无须赘言，调解率，属于司法统计中的相对指标。需要注意的是，在司法统计中，存在不同类型的调解率，如民事诉讼调解率、行政诉讼调解率，甚至刑事案件和解率。在司法统计及各级人民法院的工作报告中，调解率指向的也是民事诉讼调解率。如果对上述内容进行进一步的深化，那么，可以这样说，司法统计人员在对民事诉讼案件进行调解率计算时，还必须确定如下因素：统计时间、结案数、调解数。......
2023-08-06
-
应用统计学-统计特点和作用详细阅读
（一）统计的特点统计作为人们认识客观世界总体数量变动关系和变动规律活动的总称，具有以下特点。这是统计学区别于其他社会经济科学的根本特点。（二）统计的作用1.统计是认识世界的有力武器人们通过统计研究事物的量及其变化，去认识事物的质和事物发展的规律。......
2023-08-13
-
对应分析的原理和依据：应用多元统计分析详细阅读
，λm 对应的特征向量，且．矩阵代数的这几个结论为我们建立了因子分析中R 型与Q 型的关系．借助以上引理11．2．2和引理11．2．3，我们从R 型因子分析出发可以直接得到Q 型因子分析的结果．由于SR 和SQ 有相同的非零特征值，而这些非零特征值又表示各个公共因子所提供的方差，因此变量空间Rp 中的第一公共因子、第二公共因子…......
2023-11-18
-
电阻率的常用测试方法及原理详细阅读
图2.28电桥法图2.29伏安法2.4.3.2按照电极数量分类二相电极法。图2.30二相电极法图2.31电阻率测试装置 （长方体）四相电极法。图2.32四相电极法图2.33电阻率测试装置2.4.3.3按电源分类在目前的相关报道中，无论是采用伏安法还是电桥法基本上是直流电，也有个别采用交流电。图2.34非接触电阻率测定仪原理2.4.3.5按频率分类对于交流电测频率的选择，人们一直未作统一，不同专家学者选取不同频率。......
2023-06-26
-
显示分辨率和图像分辨率的区别和意义详细阅读
显示分辨率显示分辨率是指显示屏上能够显示出的像素数目，又称为“屏幕分辨率”。图像分辨率图像分辨率是指组成一幅图像的像素密度的度量方法。在用扫描仪扫描彩色图像时，通常要指定图像分辨率，常用的单位是DPI，表示每英寸长度图像上像素点的数量。位图图像是二维的，图像分辨率对于位图图像在水平和垂直两个方向上保持一致。图像分辨率是确定组成一幅图像的像素数目，而显示分辨率是确定显示图像的目标区域大小。......
2023-10-22
相关推荐