本章从物质循环和全生命周期的角度，借助物质流分析方法，提出了建筑物质循环系统的清洁性测度方法。物质流分析方法是一种分析经济生产活动全过程的静态分析工具。20世纪七八十年代，随着物质平衡、工业代谢等相关理论的开发和完善，推动了物质流分析方法在整个经济系统中的广泛应用。物质流分析中三大基础指标是输入指标、消耗指标、输出指标。物质输入指标是物质流分析中最为重要的指标。......
2025-09-29
明渠流水力熵与统计熵的分析
【摘要】：12.6.2.1明渠流水力熵原理对于封闭水体，如一杯晃动的水，当水体达到静平衡时，系统水力熵达到最大，熵产生率最小为零，杯中水的可用机械能最小，水的动能全部通过紊动粘性转化为热能耗散。
12.6.2.1 明渠流水力熵原理
对于封闭水体，如一杯晃动的水，当水体达到静平衡时，系统水力熵达到最大，熵产生率最小为零，杯中水的可用机械能最小，水的动能全部通过紊动粘性转化为热能耗散。明渠流为开放系统，清水明渠流包括层流和紊流，通常为紊流，可利用开放系统稳定的普适发展判据判定明渠流的稳定性。
任意取长度为ΔL 的明渠作为一个系统来分析(见图12-7)，进口断面1的流量为Q1，断面平均水力机械能为γH1+γΔZ0+γU 21/2g，出口断面2 的流量为Q2，断面平均水力机械能为γH2+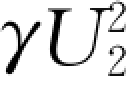
/2g，当Q1=Q2=Q 且明渠边界固定时，对体积为流量Q 的水体进行研究，系统的水力熵增(或熵差)为
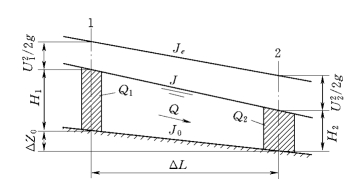
图12-7 明渠流水力熵差计算示意图
式中:ΔHe为断面1和断面2的总水头差。
式 (12-13)可理解为体积为流量Q 的水体从断面1进到断面2出的可用机械能损耗变为系统内的紊动。当系统为恒温时，紊动能通过水的粘性全部转化为热能，即系统的熵增，以熵流的形式(水蒸发和传热)传递给水流的环境，明渠流系统的熵产生率为
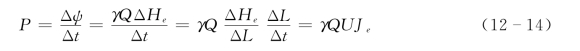
式中:γ为水的比重;Q 为流量;U 为断面平均流速;Je为能坡。
根据耗散结构原理判定开放系统稳定的普适发展判据，可得:
且当明渠流达到非平衡定态(动平衡)时
明渠流最小可用能耗率原理可表达为:在一定水流和明渠边界条件下，明渠流通过水深、流速分布和能坡的精确调整，使水流的可用机械能损耗率为最小，最小值的大小取决于水流和明渠边界条件，用式(12-15)表达。
12.6.2.2 明渠流统计熵原理
明渠流统计熵也是水力熵在微观上的统计解释，明渠流统计熵是系统的可用机械能耗散在体系中如何分配的函数，明渠流统计熵计算采用式 (12-12)。对式 (12-15)进行变换后可得到(https://www.chuimin.cn)
式中:W 为湿周;R 为水力半径;τe为剪切阻力。
对式(12-16)求微分
式(12-17)反映了湿周W、流速U 和剪切阻力τe变化的对明渠水力熵调整的贡献或分配，由于湿周W 的变化发生在水面的水边处，此处流速和剪切阻力很小，可以认为湿周的调整对明渠水力熵调整的贡献与流速和剪切阻力相比不是同量级的，则有
由式(12-18)，令
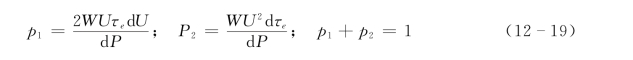
流速分布和剪切阻力在明渠系统内是可以自由调整的，由式 (12-19)可知p1和p2符合河流统计熵计算式(12-12)的要求，根据最大统计熵原理的等概率定理，当系统达到动平衡时，p1=p2，可得
对上式积分
对于均匀流，Je=J，则可推出著名的谢才公式
谢才公式是在大量的试验和观测基础上提出来的，是大量的试验和实测资料的统计结果，也就是从试验和实测资料上证明了提出的明渠流最小可用能耗率原理和式 (12-15)是正确的。这里从能耗的角度对谢才公式进行了推导和证明。
相关文章
- 详细阅读
-
电迁移中产生的熵增量对微观结构影响很大详细阅读
作为比较，在电迁移中主要的熵增来源于焦耳热：式中，jem为电流密度；φ为电势。取jem＝104 A/cm2，ρ＝10-5Ω·cm，可得其数量级与400 K温度附近1 000 K/cm温度梯度下的热迁移产生的熵增数量级相同。类似地，电迁移中其他来源的熵增都很小。因为由焦耳热或热传导产生的熵增比原子迁移产生的熵增大几个数量级，可想而知电迁移或热迁移中产生的熵增会大大影响微观结构。......
2025-09-29
-
使用3D PTV测量明渠均匀流颗粒运动规律的详细阅读
Dupont et al.采用立体摄像的3D PTV测量了0.6cm3空腔内晶体生长过程中颗粒三维运动的轨迹，作者只论证了该系统的可靠性，还没有颗粒运动规律的研究成果。本节介绍采用3D PTV试验研究明渠均匀流的颗粒运动规律，揭示出颗粒纵向平均速度符合对数分布规律，颗粒垂向的浓度分布符合Rouse方程。在近壁流区，颗粒纵向和垂向脉动速度的概率密度偏离正态分布，横向则接近正态分布。......
2025-09-29
-
推移质颗粒单步运动的统计规律分析详细阅读
分析具有代表性的6组试验的推移质颗粒的单步运动，对大量粒子的运动规律进行统计分析。图1-34典型跃移轨迹xz平面图1-33、图1-34中L 为粒子跃移的单步步长，L1为颗粒起跃至达到最高点的长度，H 为跃高，d 是颗粒单步运动横向摆动幅度，uo、vo、wo分别为起跃点的纵向、垂向和横向速度，ue、ve、we则为降落点的纵向、垂向和横向速度。......
2025-09-29
-
用数学统计法分析数据详细阅读
数理统计法有合成总库容法、直接总库容法和随机模拟法等。某多年调节水库，已知多年平均年径流量＝6000万m3、Cv＝0.6、Cs＝2Cv，年供水量W用＝4500万m3，p设＝85%。已知Cv＝0.3、Cs＝3Cv，α＝0.8，p设＝90%，求β多。因为Cs≠2Cv，故需先用式变换参数。当代表年的来水、用水确定后，就可采用年调节兴利调节计算方法确定年库容。在不计损失的基础上，可进一步计入损失。......
2025-09-29
-
建筑物质循环系统物质流分析详细阅读
1．建筑全生命周期的物质流从建筑生命周期的角度看，建筑从材料生产阶段就不断与其所处的环境进行物质资源的转化，以及物质流的运动，直到整个物质生命过程的结束。图4．1建筑生命周期物质流分析删除④流向。在建筑全生命周期循环系统中，清洁生产主要是依靠②、③和⑤这三个物质流量来实现物质流①和⑥的最小化。图4．2建筑循环系统的物质流分析......
2025-09-29
-
最大子业务流数限制对业务流程的影响分析详细阅读
由于GRSA没有任何安全策略，所以其平均信息泄露率最高。这是因为MSF值越高，机密信息被分割成的子业务流越多，进而可避免机密信息泄露，降低泄露率。对于MES-RSA，可以通过将业务分出更多的子业务流使得CIS的传输不受安全限制的影响，所以在低负载情况下其阻塞率较低。这是因为MSF值越高，CIS被分割成的子业务流越多，可以有效降低子业务流占用子载波的数量，使得一些尺寸较小的频谱碎片得到有效利用，因此可以得到更好的网络性能[25]。......
2025-09-29
-
一般性统计分析实用指南详细阅读
表3.1交通事故致因因素前10名2.交通事故空间要素统计分析按照行政分区进行统计，得到纽约市5个行政区共195个人口普查区的交通事故次数的分布，如图3.1所示。表3.2交通事故发生次数前5名的人口普查区续表图3.1纽约市交通事故空间分布图纽约市5个行政区交通事故统计见表3.3。......
2025-09-29
相关推荐