当S1 与S4 开通后，VD1 和VD4 处于通态，电感L 的电流逐渐上升；当S2 与S3 开通后，VD2 和VD3 处于通态，电感L 的电流也上升。图4.17全桥电路原理图图4.18全桥电路的理想化波形如果S1、S4 与S2、S3 的导通时间不对称，则交流电压uT 中将含有直流分量，会在变压器一次侧产生很大的直流分量，造成磁路饱和。目前，全桥变换电路广泛应用于数百瓦至数十千瓦的各种工业用开关电源中。......
2023-06-23
全沙数学模型的建立与优化
【摘要】：10.4.2.4沉降系数确定图10-16航道疏浚深度与悬沙沉降系数的关系在悬沙不平衡输沙方程和河床变形方程式中，沉降系数α 对河床冲淤强度有较大影响。
10.4.2.1 模型范围
为了反映长江河口在径流和潮流作用下的运动以及外海大范围海域的潮流形态，模型范围上游自徐六泾起至外海绿华山以远-40m 等深线、南起南汇芦潮港、北抵启东连兴港包括南、北支在内的水域，模型东西长200km、南北宽130km。采用边界拟合网格拟合河道及整治工程边界，网格数为27492个(237×116)，网格步长100～4000m (图10-14)。北支河段地形采用1992年测图，徐六泾至高桥段按1993年测图，外海-20.0m 等深线以远用1961年海图，南北槽区域按当时最新测图，其余地形采用1996年测图(图10-15)。
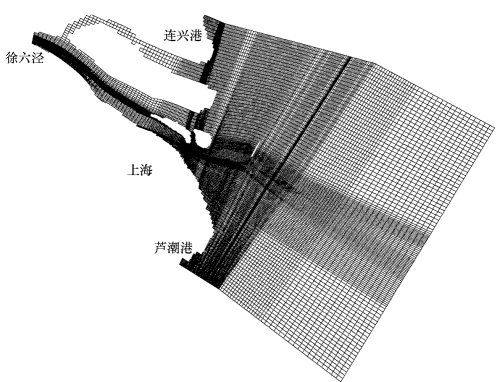
图10-14 数学模型计算网格
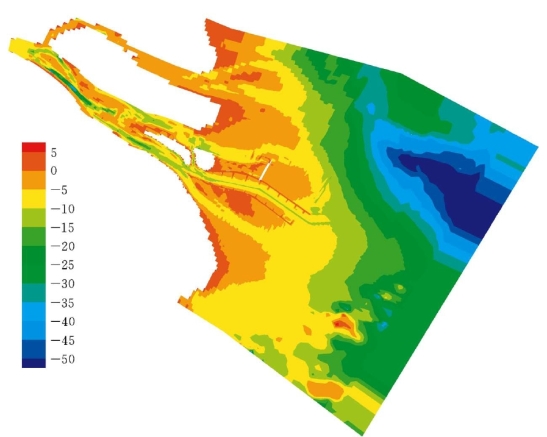
图10-15 数学模型概化地形 (二期工程)
10.4.2.2 边界条件和初始条件
长江口外海三面开敞，三个开边界分别由芦潮港、绿华山、连兴港1996年9月1～30日(洪季)和1996年2月15日～3月15日 (枯季)实测过程线按线性插值控制，上游由徐六泾和杨林站该时段实测潮位过程线的平均值控制;开边界上含沙量过程线由靠近的测点提供。外海边界含沙量取0.1kg/m3。
初始潮位取计算开始时的平均潮位，初始流速取零;含沙量初值由各测点实测初始含沙量插值得到。
10.4.2.3 参数选取
潮流数学模型计算时间步长为20s，紊动粘滞系数ν为150m2/s，糙率系数取 (从口外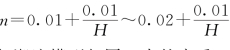
向上游按线性内插)。全沙模型计算时间步长为120s，糙率与潮流模型相同，水的容重γ=1000kg/m3，泥沙颗粒容重γs=2650kg/m3，悬移质干容重取γos=750kg/m3，推移质干容重取γob=1200kg/m3。
从徐六泾至高桥泥沙颗粒未发生絮凝，按d50=0.01mm 考虑，洪季水温较高，其沉速ω=0.0001m/s;枯季水温较低，其沉速ω=0.00008m/s。洪季上游径流较大，5‰含盐度的水体只到北槽中，15‰的水体只到北槽下口;枯季上游径流较小，5‰的水体可到南港高桥，15‰的水体可到达北槽中。根据含盐度的变化和洪、枯季水温的不同，对悬沙颗粒的絮凝沉速进行了概化，其值变化于0.00008～0.0007m/s之间。波高和波周期在验证含沙量过程线时按实测资料推求得到;在验证工程前北槽-7m 航道多年平均年疏浚量时，波高和波周期按引水船和高桥站多年平均波高和波周期 (分别为0.9m、3.7s和0.35m、2.4s)进行插值得到。取推移质d50=0.1mm，αb=0.2，k2=0.01。
10.4.2.4 沉降系数确定
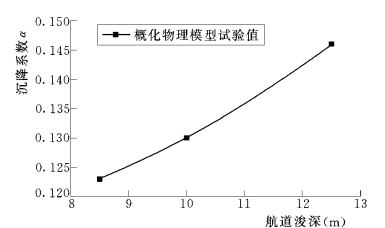
图10-16 航道疏浚深度与悬沙沉降系数的关系
在悬沙不平衡输沙方程和河床变形方程式中，沉降系数α 对河床冲淤强度有较大影响。为了解航道增深后α的变化，采用浑水动床概化物理模型进行研究。模型平面比尺为1000，垂直比尺为100，变率为10，模拟了长江口北槽近40km 的河道。模型的北边界沿横沙东滩向东，南边界沿九段沙向东，宽约10～15km。模型沙采用容重为1.48t/m3的电木粉。在模型设计中考虑了潮流相似和泥沙运动相似以保证冲淤相似。
物理模型试验表明，沉降系数α值在航道浚深至-8.5m、-10m、-12.5m和-15m 时分别为0.123、0.130、0.146和0.170，即随航道浚深而增大(图10-16)。
10.4.2.5 导堤防沙作用的表述
双导堤是长江口深水航道治理工程的主体工程。未建导堤前，由于横沙东滩和九段沙的水深较浅，风浪掀沙作用较强，滩面上的含沙量较大，在涨落潮挟带下通过北槽，致使北槽内的含沙量从上向下沿程递增。修建导堤后，当水漫过导堤时，滩地上层较清的水体进入航道，滩面附近高浓度含沙水体被挡在堤外;当堤顶露出水面时，两边滩地上的水体不与北槽水体交换，落潮水流由南港进入，涨潮水流由双导堤下口进入，北槽含沙量较小。在数学模型中应反映出导堤的防沙作用。
在不考虑滩面冲淤变化条件下，即认为滩面处于冲淤平衡，取紊动扩散系数沿水深为常值，含沙量沿垂线分布变化可表述为
式中:s为距离床面z 点处的含沙量;s0为z=0点的河底含沙量;m 为悬浮指数;h 为水深。
通过对上式积分，可分别求出垂线平均含沙量sm和越堤水流的平均含沙量sΔz与河底含沙量s0的关系，即
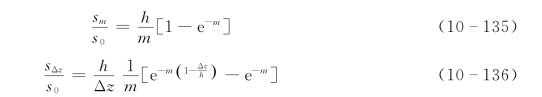
式中:Δz为堤顶潮流厚度。
由此求得漫堤流平均含沙量与全水深平均含沙量之比值，即
根据现场泥沙观测资料，可以得到垂线平均含沙量与河底含沙量的比值，通过式(10-135)可以求出悬浮指数m，再利用式(10-137)即可得到不同堤顶漫水厚度条件下的平均含沙量，此即为越堤进入北槽的含沙量。通过这种近似处理，将滩面附近的高浓度泥沙挡在双导堤之外，反映了导堤的防沙作用。
有关泥沙研究进展的文章
- 详细阅读
- 详细阅读
-
水文地质勘察（第2版）论述数学模型的选择与建详细阅读
11.6.6.2 计算方法与步骤1.数学模型的选择数学模型的建立,既要考虑需要,又要分析实际问题的复杂程度是否具有所选模型相应的资料。......
2023-09-18
- 详细阅读
-
频率动态仿真误差模型的建立与优化详细阅读
基于上述定义的频率动态轨迹的特征指标，建立误差模型函数。依据所研究的频率动态问题，分别在每组确定的系统参数下，首先选取若干个有实际参考意义的频率实测轨迹；其次利用电力系统仿真软件仿真得到频率仿真轨迹；然后通过上述已建立的单功率脱落事件下的误差模型计算误差值，并对这些样本进行两两比较，形成判断矩阵；最后通过对判断矩阵进行求解，得到各个样本的权重系数。......
2023-06-29
-
数学模型基本框架优化详细阅读
5.2.1.2模型参数计算方法在式、式中， 为河道的泥沙综合恢复饱和系数，它与河道断面形态，冲淤状态及水流泥沙运动参数有关，βs为反映断面流速和输沙不均匀分布的系数。......
2023-06-22
-
沟道输沙计算优化方法详细阅读
因而，为区分侵蚀与产沙的不同概念，以使模型的建立符合流域泥沙运动的基本物理图景，沟道输沙模型应采用不平衡输沙模式。不平衡输沙的结果将能够反映河网范围内不同位置的冲淤分布，以及各河段的冲淤变化过程。上式的积分形式为河段出口含沙量的显式计算公式式中:Sx、Sx*分别为断面的平均含沙量和水流挟沙力;q 为单宽流量;α 为恢复饱和系数。为充分考虑高含沙量的影响，雷诺数Re 基于含沙水流的粘度μ 计算 。......
2023-06-22
-
数学模型计算结果优化详细阅读
图13-24异重流潜入位置变化过程表13-7水库运用初期1～5年库区输沙计算结果图13-24异重流潜入位置变化过程表13-7水库运用初期1～5年库区输沙计算结果在相同的水沙条件及边界条件下进行的小浪底库区实体模型试验结果表明，距坝67km 以下库段总淤积量为29.44 亿m3，若淤积物干容重γ0=1.15t/m3，则淤积量为33.8亿t。......
2023-06-23
相关推荐