为保证异重流运动相似，张俊华等、李书霞等 以非恒定异重流运动方程式开展相似分析，并通过水库泥沙模型检验，得出的异重流发生相似条件，利用二维非恒定非均匀流的扩散方程得到异重流挟沙相似条件及异重流连续相似条件分别为:上述公式构成了完整的河道及水库模型相似律。上述公式构成了完整的河道及水库模型相似律。......
2023-06-23
波浪相似条件的探讨
【摘要】：10.2.2.2波浪传质速度相似上述波浪中的水质点运动是封闭的，但事实上水还是有少量的传输。
10.2.2.1 波动速度相似
根据线性波理论，在有限水深条件下各层波动水质点速度在水平方向的分量Uw、垂直方向的分量WW以及波速CW和波周期T 分别为
式中:h0为基面以下水深;z为位于基面上的垂直坐标，当z 位于水面时，水深h=h0+z，当处于海底时z=-h0;x 和t分别为讨论点的位置和时间。
上述各式表明，只有当波高比尺与波长比尺相同且均等于水深比尺时，模型与原型的波浪质点速度才能相似，即波浪比尺需按水深比尺取成正态。因此取
式中:h0为基面以下水深;z为位于基面上的垂直坐标，当z 位于水面时，水深h=h0+z，当处于海底时z=-h0;x 和t分别为讨论点的位置和时间。
上述各式表明，只有当波高比尺与波长比尺相同且均等于水深比尺时，模型与原型的波浪质点速度才能相似，即波浪比尺需按水深比尺取成正态。因此取
由式(10-62)、式(10-63)、式 (10-64)和式 (10-65)可以得出各量的相似比尺
由式(10-62)、式(10-63)、式 (10-64)和式 (10-65)可以得出各量的相似比尺
上述相似比尺表明，波浪水平质点速度比尺不仅与垂直质点速度比尺相同，还与波速比尺和水流水平速度比尺相同;但波浪的垂直速度比尺与水流的垂直速度比尺不同，波周期比尺与水流时间比尺也不相同。
10.2.2.2 波浪传质速度相似
上述波浪中的水质点运动是封闭的，但事实上水还是有少量的传输。Stokes二阶有限振幅理论能够描述这个问题。在有限水深条件下波浪传质速度UT的计算公式为
上述相似比尺表明，波浪水平质点速度比尺不仅与垂直质点速度比尺相同，还与波速比尺和水流水平速度比尺相同;但波浪的垂直速度比尺与水流的垂直速度比尺不同，波周期比尺与水流时间比尺也不相同。
10.2.2.2 波浪传质速度相似
上述波浪中的水质点运动是封闭的，但事实上水还是有少量的传输。Stokes二阶有限振幅理论能够描述这个问题。在有限水深条件下波浪传质速度UT的计算公式为
当波高比尺与波长比尺相同并均为水深比尺时，由上式可得波浪传质速度比尺为
当波高比尺与波长比尺相同并均为水深比尺时，由上式可得波浪传质速度比尺为
即与波浪质点速度和水流平面速度的比尺相同。
10.2.2.3 波浪折射相似
波浪在由深水区向浅水区传播过程中将发生折射。当波浪斜向进入浅水区时，由于深水处的波速和波长较大，波浪逐渐转向，波峰线逐渐趋向于与等深线平行。在传播过程中，波周期变化较小，可以认为是常值，因而有
即与波浪质点速度和水流平面速度的比尺相同。
10.2.2.3 波浪折射相似
波浪在由深水区向浅水区传播过程中将发生折射。当波浪斜向进入浅水区时，由于深水处的波速和波长较大，波浪逐渐转向，波峰线逐渐趋向于与等深线平行。在传播过程中，波周期变化较小，可以认为是常值，因而有
式中:α0和α分别为深水处的入射角和浅水处的折射角。
在折射过程中表述波高变化的关系式为
式中:α0和α分别为深水处的入射角和浅水处的折射角。
在折射过程中表述波高变化的关系式为
由于变态模型中已取波高和波长比尺均为水深比尺，故从上述各式可得
由于变态模型中已取波高和波长比尺均为水深比尺，故从上述各式可得
上述相似比尺表明，变态模型中的波浪折射情况与原型相似。
10.2.2.4 波浪绕射相似
波浪在传播过程中遇有建筑物时将发生绕射。如仍用H0表示绕射前的深水波高，则经绕射后的波高H 可由下式表述:
上述相似比尺表明，变态模型中的波浪折射情况与原型相似。
10.2.2.4 波浪绕射相似
波浪在传播过程中遇有建筑物时将发生绕射。如仍用H0表示绕射前的深水波高，则经绕射后的波高H 可由下式表述:
其中:Kr为绕射系数，其值为下述复变函数F(x，y)的模
其中:Kr为绕射系数，其值为下述复变函数F(x，y)的模
其中:
其中:
在上述绕射公式中包含着y/L 和 x 2+y 2/L 值，其分子分母中的长度具有不同的比尺，因而变态模型中的波浪绕射情况不能与原型完全相似，只能允许其有一定偏离。至于多大变率引起的偏离才可以接受，只有依靠试验来明确。
10.2.2.5 波浪破碎相似
波浪传至岸边附近浅水区域时将发生破碎，其破碎水深(或破碎位置)与波高、波长和岸滩坡度等有关。日本《港口建筑物设计标准》依据大量试验资料，将Hb/hb与hb/L0的关系绘制成以岸滩坡度m 值为参数的曲线组。窦国仁将此曲线组概括为如下的表述式:
在上述绕射公式中包含着y/L 和 x 2+y 2/L 值，其分子分母中的长度具有不同的比尺，因而变态模型中的波浪绕射情况不能与原型完全相似，只能允许其有一定偏离。至于多大变率引起的偏离才可以接受，只有依靠试验来明确。
10.2.2.5 波浪破碎相似
波浪传至岸边附近浅水区域时将发生破碎，其破碎水深(或破碎位置)与波高、波长和岸滩坡度等有关。日本《港口建筑物设计标准》依据大量试验资料，将Hb/hb与hb/L0的关系绘制成以岸滩坡度m 值为参数的曲线组。窦国仁将此曲线组概括为如下的表述式:
其中:
其中:
这里m 为岸滩坡度。式(10-83)表明，当岸滩坡度大于1/50时，破碎波高与破碎水深之比值与岸滩坡度有关;当岸滩坡度等于或小于1/50时，该比值则与岸滩坡度无关，仅只与hb/L0有关;当hb/L0很小时，Hb/hb值不再随hb/L0的减小而增大并趋于常值，对于m≤1/50时，该极限值为
这里m 为岸滩坡度。式(10-83)表明，当岸滩坡度大于1/50时，破碎波高与破碎水深之比值与岸滩坡度有关;当岸滩坡度等于或小于1/50时，该比值则与岸滩坡度无关，仅只与hb/L0有关;当hb/L0很小时，Hb/hb值不再随hb/L0的减小而增大并趋于常值，对于m≤1/50时，该极限值为
一般情况下，粉沙和淤泥质岸滩的坡度均远小于1/50。因而对于这类岸滩波浪发生破碎的位置在变态模型中仍能与原型相似。由此得模型的允许变率为
一般情况下，粉沙和淤泥质岸滩的坡度均远小于1/50。因而对于这类岸滩波浪发生破碎的位置在变态模型中仍能与原型相似。由此得模型的允许变率为
式中:mp为原型岸滩坡度。
例如原型岸滩坡度为1/500时，模型的变率应远远小于10。
在破波带中，破波类型主要取决于岸滩坡度和波陡，其判别数Ir为
式中:mp为原型岸滩坡度。
例如原型岸滩坡度为1/500时，模型的变率应远远小于10。
在破波带中，破波类型主要取决于岸滩坡度和波陡，其判别数Ir为
式中:Hl和Ll为波浪破碎前的波高和波长。
当Ir＞3.3时，破波为溃波型;当3.3＞Ir＞0.5时，破波为卷波型;当Ir＜0.5时，破波为溅波型。对于岸滩波度较缓的粉沙淤泥质河口和海岸带，Ir值一般远远小于0.5，故在变态模型中破波类型仍能与原型相似，即均属于溅波型破波。由此得模型的允许变率为
式中:Hl和Ll为波浪破碎前的波高和波长。
当Ir＞3.3时，破波为溃波型;当3.3＞Ir＞0.5时，破波为卷波型;当Ir＜0.5时，破波为溅波型。对于岸滩波度较缓的粉沙淤泥质河口和海岸带，Ir值一般远远小于0.5，故在变态模型中破波类型仍能与原型相似，即均属于溅波型破波。由此得模型的允许变率为
10.2.2.6 沿岸流相似
当波浪斜向传至浅水区时将发生破碎并产生沿岸流。表述沿岸流流速的公式较多，其中由P.D.Komar修改后的Longuet-Higgins公式为
10.2.2.6 沿岸流相似
当波浪斜向传至浅水区时将发生破碎并产生沿岸流。表述沿岸流流速的公式较多，其中由P.D.Komar修改后的Longuet-Higgins公式为
式中:ul为沿岸流的平均流速;θb为破波波峰线与岸线间的夹角(锐角)。
由于变态模型中的折射与原型相似，因而模型中的θb与原型中的θb相同，故得
式中:ul为沿岸流的平均流速;θb为破波波峰线与岸线间的夹角(锐角)。
由于变态模型中的折射与原型相似，因而模型中的θb与原型中的θb相同，故得
即沿岸流的流速比尺与水流流速比尺相同。如采用P.S.Eagleson的公式，也可得到相同结果。
即沿岸流的流速比尺与水流流速比尺相同。如采用P.S.Eagleson的公式，也可得到相同结果。
式中:fw为波浪摩阻系数，破波带波群速与波速的比值
式中:fw为波浪摩阻系数，破波带波群速与波速的比值
由于波高与波长的比尺相同，故nb的比尺等于1。波浪阻力系数fw与无量纲谢才系数C0的平方成反比，而在阻力相似条件下由式 (10-61)可知C0的比尺等于变率的开方，故有
由于波高与波长的比尺相同，故nb的比尺等于1。波浪阻力系数fw与无量纲谢才系数C0的平方成反比，而在阻力相似条件下由式 (10-61)可知C0的比尺等于变率的开方，故有
而岸滩坡度m 的比尺
而岸滩坡度m 的比尺
故从式(10-89)也可得到λul=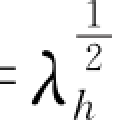
，即与潮流流速比尺相同。由此可见，变态模型中的沿岸流与原型可以相似。
综上所述，在变态模型中，取波高比尺与波长比尺相同且均等于水深比尺时，对于坡度较缓的海岸和河口，可以达到波浪质点速度、传质速度、波速、波群速、波浪折射、波浪破碎的位置、类型和沿岸流等的相似，但在波浪绕射方面有一定的偏离。
故从式(10-89)也可得到λul=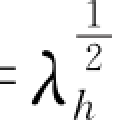
，即与潮流流速比尺相同。由此可见，变态模型中的沿岸流与原型可以相似。
综上所述，在变态模型中，取波高比尺与波长比尺相同且均等于水深比尺时，对于坡度较缓的海岸和河口，可以达到波浪质点速度、传质速度、波速、波群速、波浪折射、波浪破碎的位置、类型和沿岸流等的相似，但在波浪绕射方面有一定的偏离。
有关泥沙研究进展的文章
- 详细阅读
- 详细阅读
-
底沙的相似条件探析详细阅读
式要求以全水深表示的底沙浓度比尺应等于其输沙能力比尺。由式和式可知，这就是要求底沙输沙量比尺与底沙输沙能力比尺相同，即即底沙的沉速比尺与悬沙的沉速比尺式完全相同，且均与水流的垂直流速比尺式相同。由式可以得出输移底沙的水流时间比尺为它与式表述的含沙量比尺完全相同。由式可以写出由底沙引起的冲淤时间比尺λtb为即与潮流时间比尺式相同，也与输移悬沙的水流时间比尺一致。......
2023-06-22
-
合作供给均衡条件优化与探讨详细阅读
小型水利设施的合作属于集体行为问题，而集体行动供给过程中容易出现“搭便车”现象。因此，有必要寻找一个委托代理人来对农户合作行为进行激励，委托他作为合作供给组织的发起者，维护农户间的合作。因此，通过人为设计小型水利设施合作供给制度，诱导农户进行自发合作供给是保障小型水利设施的有效途径。青木昌彦通过对村庄的灌溉系统中搭便车问题的分析发现多个主体博弈有利于放宽激励约束条件。......
2023-06-28
-
矩阵相似对角化条件及意义详细阅读
【主要内容】1.矩阵可相似对角化的定义设A是n阶矩阵，如果它与n阶对角矩阵Λ相似，则称A可化为相似的对角矩阵，简称A可相似对角化.n阶矩阵A可相似对角化的条件：（1）A有n个互异的特征值是A可相似对角化的充分而非必要条件.（2）A是实对称矩阵是A可相似对角化的充分而非必要条件.（3）A有n个线性无关的特征向量是A可相似对角化的充分必要条件.（4）A的每个ni重特征值λi的特征矩阵λiEn-A都满足......
2023-10-27
-
圆轴扭转的强度条件优化探讨详细阅读
圆轴扭转时横截面上的最大工作切应力τmax不得超过材料的许用切应力[τ]，即式称为圆轴扭转时的强度条件。对于等截面圆轴，从轴的受力情况或由扭矩图可以确定最大扭矩Tmax，最大切应力τmax发生于Tmax所在截面的边缘上。因而强度条件可改写为对于变截面杆，如阶梯轴、圆锥形杆等，Wt不是常量，τmax并不一定发生在扭矩为极值Tmax的截面上，这要综合考虑扭矩T和抗扭截面系数Wt两者的变化情况来确定τmax。......
2023-06-16
-
建筑及空调风机工程设计、使用与维修的相似条件详细阅读
几何相似 这是指模型与实物的几何形状相同，对应的线性长度比为一定值，对应角度相等。几何相似是运动相似的先决条件。根据气体流动的气动热力过程及能量传递过程的相似要求，两个通风机的气流过程相似条件可归结如下：几何相似、叶片进口的速度三角形相似、雷诺数相等。下面将证明只要满足上述相似条件，两个通风机一定是相似的。......
2023-08-20
-
基于Boltzmann方程的颗粒流模型的适用详细阅读
快速颗粒流是层移质运动和水石流的概化模型，是高含沙水流运动的一种极端情形。这些水沙两相之间的复杂作用不仅影响着泥沙颗粒的运动特征，还可能影响到泥沙颗粒的应力应变本构关系。同时，也有研究人员用快速颗粒流理论的成果分析高含沙水流的运动特征。本节从颗粒流理论的经典方法出发，分析快速颗粒流理论在高含沙水流运动中的适用条件。因此，本节分析液相水流所直接影响的颗粒相脉动量的本构关系。......
2023-06-22
相关推荐