在上部流区则因水流的紊动减弱而使颗粒的紊动强度明显减小。图1-56颗粒因克服当地阻力而损失的能量1.3.3.2粒径的影响1.紊动强度的变化实测的紊动强度资料见表1-23，图1-57为颗粒三个方向脉动速度的紊动强度及紊动能量沿垂线的分布。......
2025-09-29
全动床复式河槽的水沙特性分析
【摘要】：全动床复式河槽由两个对称的滩地及主槽组成，水槽长50m，宽度6m，深1m，由中值粒径为0.8mm 的天然沙均匀构筑而成。图9-20全动床复式河槽初始断面形态全动床复式河槽水槽试验研究:河道完全粗化后能量损失、阻力系数沿程变化，推移质输沙率的变化特性，床沙中值粒径的横向变化与沿程变化等。这种趋势可以表达为图9-21不同坡度的沿程变化归槽水流;漫滩水流图9-23为清水作用下全动床复式河槽输沙率随时间的变化关系图。
全动床复式河槽由两个对称的滩地及主槽组成，水槽长50m，宽度6m，深1m，由中值粒径为0.8mm 的天然沙均匀构筑而成。为了使河道床面形态充分发展，主槽泥沙厚度为14cm。另外，主槽边坡sm为1.75，主槽底宽为0.60m，每侧滩地宽度为0.85m，滩槽高差为0.20m，如图9-20所示。复式河槽长31m，其中试验动床段长27m，粗卵石过渡段长4m。过渡前设置了3m 长的消能段。这里考虑了两个流量 (0.080m3/s 和0.180m3/s)，一个为归槽水流流量，另一个为漫滩流量。每组试验河道初始底坡均为2‰(杨克君，2006)。
图9-20 全动床复式河槽初始断面形态
全动床复式河槽水槽试验研究:河道完全粗化后能量损失、阻力系数沿程变化，推移质输沙率的变化特性，床沙中值粒径的横向变化与沿程变化等。如果以水面坡度代替能坡，是会产生误差的。阻力系数与能坡的沿程变化趋势是相似的，而这种沿程变化趋势又与床沙代表粒径变化趋势总体相一致。不同坡度的沿程变化如图9-21所示，阻力系数的沿程变化如图9-22所示。
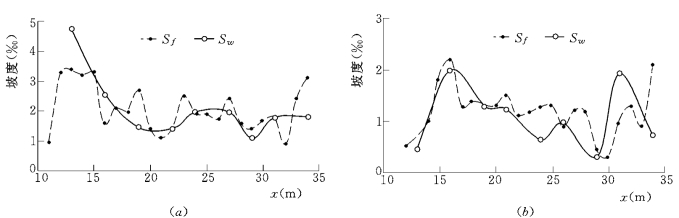
图9-21 不同坡度的沿程变化
(a)归槽水流;(b)漫滩水流
图9-23为清水作用下全动床复式河槽输沙率随时间的变化关系图。从该图可以看出，在清水作用下，输沙率表现出两种趋势，即先随时间单调递增，而后随时间单调递减。这种趋势可以表达为
图9-22 阻力系数的沿程变化
(a)归槽水流;(b)漫滩水流
即
图9-23 输沙率随时间的变化特性(https://www.chuimin.cn)
河道急剧展宽发生在清水作用初期，而且作用时间很短。在特定的试验条件下，全动床复式河槽滩岸侵蚀速率在空间上变化趋势为:越往下游，同流量下的滩岸侵蚀速度越小。与初始河道相比，主槽床面沿程始终处于淤积状态，而主槽两侧均处于冲刷状态。冲刷或淤积面积均有沿程减小的趋势，这与流速总体沿程减小相一致。尽管初始断面是对称的，床沙初始级配是相同的，但主槽两侧断面冲刷面积并不相等。
运用仙农熵 (Shnnon Entropy)的概念与理论，推导了清水作用下粗化过程中推移质输沙率公式。
无论是输沙率单调递增段还是单调递减段，推移质输沙率公式都具有相同的表达形式。
据此，导出了随机变量X 表达式的一般形式。假如Y 属于区间 [A，B]。根据随机变量X 在区间[A，B]上的变化特点，可以将区间分为N 个单调区域，则式 (9-34)也可以表达为
假定这里讨论的随机变量(如输沙率，粒径，纵向流速，稳定床面的横向坡度等)均为正的那类，即X＞0，从式(9-35)可知
这说明，参数ki的取值与曲线X =X(Y)凹凸的关系。若曲线上凹，ki取负值;反之，若曲线上凸，ki取正值。
推移质输沙率计算结果与实测结果如图9-24所示。
图9-24 清水冲刷过程中推移质输沙率随时间变化
(a)归槽水流;(b)漫滩水流
无论是归槽水流还是漫滩水流，推移质中值粒径均有先随时间大幅度增大的趋势，后随着时间的增加中值粒径增加的幅度减小，最终将趋于某一恒定的值。这种变化特性可用X 一般形式的表达式进行预测。全动床复式河槽推移质运动不仅存在纵向的沿程分选，还存在横向的沿断面分选。
另外，Liu et al. (2005b)在小型水槽也进行了全动床复式河槽的试验研究。根据水槽复式断面动床实测资料，分析垂线流速和紊动强度分布，以及处于稳定状态的断面形态分布。在某一相对高度以上，垂线流速服从对数分布。在该相对高度以下，流速随水深线性变化。对于不同的流量，纵向、横向和垂向紊动强度具有相似性。先随着水深的增加而增强，当到过最大紊动强度后，其变化趋势相反。经过四个流量连续作用后处于稳定状态的床面形态也进行了分析。在河宽调整的过程中，由于清水作用，主槽淤积和主槽边坡与滩地冲刷。通过分析发现，处于稳定状态的床面形态满足抛物线分布。
相关文章
- 详细阅读
- 详细阅读
-
分析EPC系统的动态特性详细阅读
由系统的传递函数框图可得EPC系统的开环传递函数为式中 k——开环放大系数，。将算得的ωh、ξh、k代入式，可据此画出EPC系统的开环伯德图。图12-18 改造前后CP机组EPC系统的开环伯德图由图12-18可得系统的性能指标为：①穿越频率：ωc=2.4Hz；②幅值裕量：h=16dB；③相位裕度：γ=75°。可见实测值和理论分析值比较接近，说明上面建立的EPC系统的数学模型和确定的参数是正确的，是可以作为预测改造后系统性能的依据的。......
2025-09-29
-
山区河流水沙基本特性探析详细阅读
山区河流复杂的水文泥沙特性可以川江为例。川江自宜宾至宜昌全长1045km，为山区河流。表9-1川江河段平均水文特征值表山区河流水沙运动的非恒定性、卵石运动的随机性和间歇性是山区河流的突出特点。......
2025-09-29
-
各位置平面投影的特性分析详细阅读
前两种属于特殊位置平面。两投影均为原图形的“类似形”。图2-49与投影面的垂直的平面的投影特性铅垂面；正垂面；侧垂面2.5.2.3一般位置平面一般位置平面指与H、V、W 均倾斜的平面，其投影特点是：V、H、W 投影均为原图形的“类似形”，任一投影均不能直接反映出平面与某投影面的夹角，也不能直接反映出平面的实形。......
2025-09-29
-
开断特性仿真分析详细阅读
图8-3为额定电流为16A的微型断路器，当短路电流通过瞬动电磁铁线圈时，铁心向左移动，顶动脱扣杆，使机构脱扣。图8-3 微型断路器现对上述微型断路器描述其仿真过程。为了验证计算准确性，在预期电流Ip=10.2kA，U=232V，cosφ=0°，βv=4.5257×10-7条件下进行了开断试验，试验结果与计算机仿真进行了对比，如图8-7所示。......
2025-09-29
-
动触头受电动斥力分析详细阅读
如上所述，在触头未斥开前，作用在动触头上的电动斥力包括触头间由于电流收缩产生霍姆力FH和导电回路产生的洛伦兹力FL。断路器导电回路上洛伦兹力FL一直存在至电弧熄灭，与电流的平方近似成正比关系。忽略涡流的影响，采用恒定场的方程来计算电流密度和磁通密度的分布，这样可以分三步来完成电动斥力的计算。图2-17 洛伦兹力计算流程图而对于低压断路器来说，动触头一般是在一个对转动轴的力矩M的作用下打开的，如图2-18所示。......
2025-09-29
-
典型装甲目标的特性分析详细阅读
图4.1披挂ERA的主战坦克图4.2ERA抗弹防护原理目前，俄罗斯、美国、德国、英国、法国、以色列、中国等国均已发展了系列化ERA，其中又以俄罗斯“接触/K”系列ERA最具代表性。图4.6美国“福特”级航母结构布局现代大中型......
2025-09-29
相关推荐