复式河槽阻力系数分析

2023-06-22 理论教育版权反馈

【摘要】：该研究表明:9.3.1.2阻力系数阻力系数在估算复式河槽过流能力、平均流速和确定垂线平均流速横向分布等方面起着重要作用。在光滑复式河槽中，滩槽局部阻力系数基本上为常数，但大小不同。对于滩槽粗糙不同的或非对称的复式河槽，滩地的局部阻力系数不再保持不变。对于所有系列而言，滩槽局部阻力系数都将随着相对水深的增加而减小。

9.3.1.1　漫滩河道紊流横向扩散特性

复式河道是天然河流中常见的河流类型，其水流泥沙运动与单一河道明显不同。当水流由主槽漫入边滩后，不仅是过流断面发生了改变，而且水流流态也发生了改变。复式河道水流具有明显的三维特性，各种水流参数(如流速、切力、扩散系数等)均随空间位置不同而各异。通常，实际应用时，更关心的是这些参数沿边界和横向的变化(断面形态如图9-10所示)。刘兴年和Knight(2000)，Liu et al. (1999)引用了大量的SERC—FCF(英国科学工程研究会洪水水槽)试验资料分析了漫滩河道紊流横向扩散特性。

1.单一河道紊流扩散系数的横向变化

在单一河槽中，河道紊流扩散系数是水流平均流速u、水深h、水面宽度w、摩阻流速u*、水密度ρ和粘性系数μ 的函数，可表示为:

通过量纲分析得:

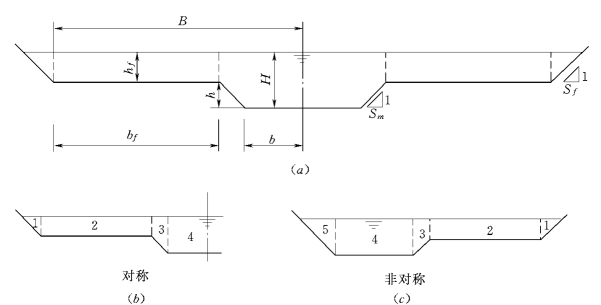
pagenumber_ebook=446,pagenumber_book=430

图9-10　复式河槽断面形态及区域分划

pagenumber_ebook=446,pagenumber_book=430

图9-11　无量纲紊流扩散系数ε/(u*h)和相对宽度、阻力系数的关系

2.漫滩河道紊流扩散系数的横向变化试验成果

试验在英国HR WALLINGFORD、伯明翰大学和四川大学进行，水槽宽度2m 和10m。水深0.1～0.7m，相对水深0.05～0.5。紊流扩散系数:

pagenumber_ebook=446,pagenumber_book=430

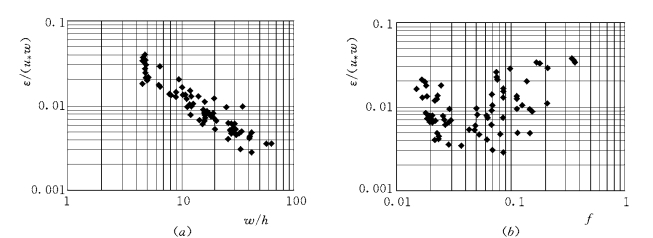
pagenumber_ebook=447,pagenumber_book=431

图9-12　无量纲紊流扩散系数ε/(u*w)和相对宽度、阻力系数的关系

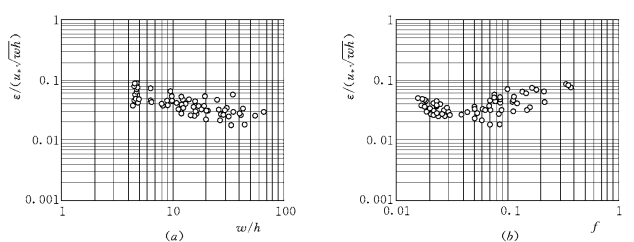
pagenumber_ebook=447,pagenumber_book=431

图9-13　无量纲紊流扩散系数ε/(u*wh)和相对宽度、阻力系数的关系

根据试验资料，点绘漫滩河道紊流扩散系数的横向变化，如图9-14所示。由此可见，当相对水深Dr=(H-h)/H 较小时，漫滩部分的紊流扩散系数比主槽大得多。随着相对水深加大，漫滩与主槽的紊流扩散系数渐渐接近。主槽水流紊流扩散系数和相对水深的关系，近乎为常数0.07。

3.漫滩河道相对宽度、深度对紊流扩散系数的横向变化的影响

pagenumber_ebook=447,pagenumber_book=431

9.3.1.2　阻力系数

阻力系数在估算复式河槽过流能力、平均流速和确定垂线平均流速横向分布等方面起着重要作用。Yang et al. (2005)通过分析SERC-FCF的大量的试验资料 (其断面形态如图9-10所示)，建立了达西—韦斯巴赫综合阻力系数、局部阻力系数及曼宁系数与不同断面形态、不同床面粗糙度的关系，并分析了传统方法不能正确估算过流能力的原因在于:传统方法忽略了滩槽交界面的表观切应力(其实质是增大了附加阻力)。该研究表明:

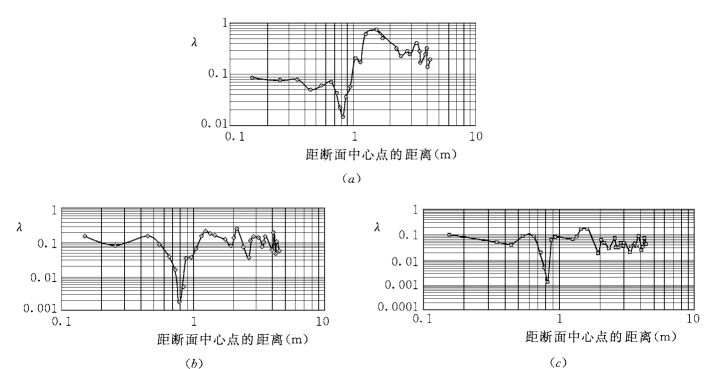
pagenumber_ebook=448,pagenumber_book=432

图9-14　漫滩河道紊流扩散系数的横向变化

(a)SERC-FCF 010201(Dr=0.10 和B/b=6.67);(b)SERC-FCF 010401(Dr=0.2 和B/b=6.67);
(c)SERC-FCF 010601(Dr=0.2 和B/b=6.67)

(1)复式河槽达西—韦斯巴赫局部阻力系数与滩槽宽度比、主槽边坡、对称性、滩地粗糙度等有关。在光滑复式河槽中，滩槽局部阻力系数基本上为常数，但大小不同。对于滩槽粗糙不同的或非对称的复式河槽，滩地的局部阻力系数不再保持不变。对于所有系列而言，滩槽局部阻力系数都将随着相对水深的增加而减小。

(2)二次流将影响垂线平均流速及床面剪切应力的横向分布，如图9-15所示。如果忽略二次流，滩槽床面平均剪切应力相对误差分别为17.6%、15.3%;如果考虑二次流，则滩槽相滩误差的平均值将减至4.4%与4.3% (Liu et al.，2005c)。

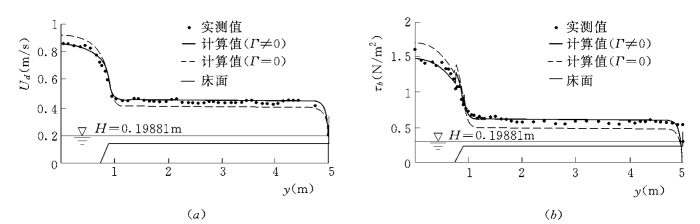
pagenumber_ebook=448,pagenumber_book=432

图9-15　二次流对垂线平均流速及床面剪应力横向分布的影响(阻力系数采用实测值，λi均取0.13，SERC-FCF 010501)

(a)垂线平均流速横向分布;(b)床面剪切应力横向分布

(3)复式河槽滩地、主槽曼宁阻力系数也分别与滩槽宽度比、主槽边坡、对称性、滩槽床面粗糙差别等有关。对于所有系列而言，基本上存在相同的变化趋势:滩地糙率(nf)、综合糙率(nc)都是先随着相对水深的增加而减小，后随着相对水深的增加而增大;而主槽糙率(nm)变化趋势则相反。与床面粗糙度相同的单一河槽相比，基本上是复式河槽的滩地曼宁阻力系数比单一河槽的小，而主槽的比单一河槽的大，如图9-16所示。

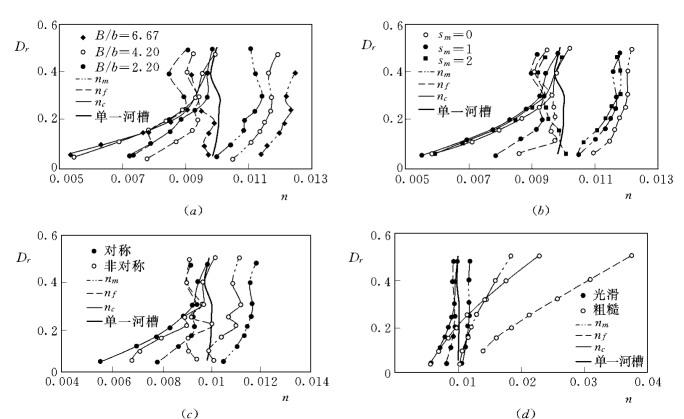
pagenumber_ebook=449,pagenumber_book=433

图9-16　曼宁阻力系数受相对水深、滩槽宽度、主槽边坡、光滑与粗糙复式河槽等的影响

(a)曼宁阻力系数随相对水深和滩槽宽度比的变化;(b)主槽边坡对曼宁阻力系数的影响;(c)非对称性对曼宁系数的影响;(d)光滑与粗糙复式河槽的曼宁阻力系数随相对水深的变化

9.3.1.3　复式河槽阻力系数

SERC-FCF的试验资料表明尽管断面形态不同，但主槽区[即图9-10 (b)的区域4]平均Darcy-Weisbach 阻力系数f4，随相对水深的变化趋势是相似的，如图9-17(a)。当Dr＜0.25，f4随着相对水深的增加而增加。当Dr＞0.25时，f4的变化趋势却相反，即随着相对水深的增加而减小。因此，主槽区Darcy-Weisbach 阻力系数f4，与相对水深为Dr=0.25时的阻力系数f4(0.25)的比值遵循某种关系。图9-17 (b)表明对于SERC-FCF 的试验资料而言，它们的比值满足抛物线分布。图9-17 (c)表明，对于所有不同的断面形态，滩槽平均阻力系数之比与相对水深有关，均随着相对水深的增加而减小(杨克君等，2005b)。

复式河槽阻力系数分析

相关推荐