分析具有代表性的6组试验的推移质颗粒的单步运动，对大量粒子的运动规律进行统计分析。图1-34典型跃移轨迹xz平面图1-33、图1-34中L 为粒子跃移的单步步长，L1为颗粒起跃至达到最高点的长度，H 为跃高，d 是颗粒单步运动横向摆动幅度，uo、vo、wo分别为起跃点的纵向、垂向和横向速度，ue、ve、we则为降落点的纵向、垂向和横向速度。......
2023-06-22
推移质运动的特点及应用
【摘要】：由实际资料适线，得K1=1.15，K2=10，则式中:K1、K2为待定系数。
9.2.2.1 非均匀泥沙起动
对于泥沙起动临界条件的表达方式，传统上有两种方法，即起动切力和起动流速，两者既是统一的，也存在明显的差异。起动切力具有明显的、直接的物理意义，但实测时难以获得准确的坡度资料和床面切力资料，因此在实际应用时相对困难一些。起动流速虽作为间接的起动因子，但以其天然河流中易于观测(平均流速)而独具优势，起动流速的表达方式得到更为广泛的应用。
然而，宽级配非均匀沙的起动复杂，特别是处于冲淤交替过程中的非均匀床沙的起动更是具有特殊性，有许多问题有待进一步深入探讨。每一条河流由于其来水来沙条件的不同，床沙起动的补给条件不同;即使是同一条河流在枯水期和汛期，汛前和汛后，洪峰前和洪峰后，其床沙的位置特性也不尽相同。因而目前已有非均匀沙起动流速公式还不能概括这些与粗化细化过程有关的起动流速特点，需要在卵石河道冲淤计算中考虑补给条件不同对非均匀沙起动流速的影响特性。
1.补给不足对非均匀沙起动特性影响分析
均匀床沙在一定的水流条件下，可能处于静止、部分可动和全部可动状况。非均匀沙某级粒径的临界可动条件不仅与水流条件有关，也与泥沙级配组成有关，还与床沙位置、上游来沙有密切的关系。各条河流的水沙过程和床沙组成不同，致使其床沙粗化状态也不尽相同，因此临界起动条件亦具有相异的特点。以水槽试验为例，把非均匀沙 (宽级配)铺在床面上，放入流量Q 的清水(流速为U)，清水冲刷床面至达到粗化稳定层形成;停水，然后再放入同一流量Q 的清水，则水槽中的床沙将会保持不动。再停水，可获取床沙表层粗化层级配，按此级配重新配沙铺在水槽中，并放入同样水流，则部分细沙会被起动输移。这就反映出同样水流条件和床沙级配下，由于床沙位置不同，而产生了起动流速不同。目前的临界起动公式还不能概括上述现象。
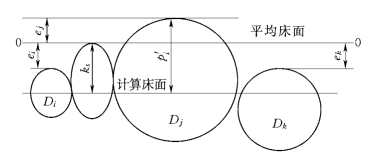
图9-6 床沙暴露度示意图
在卵石浅滩整治工程中河道冲刷计算时，由于上游补给条件的不同，整治河段可能出现冲淤交替而产生床沙位置特性经常变化。同样，不同的河流，由于来水来沙条件各异，床沙的位置特性也不尽相同。因此，应考虑床沙特性如何影响非均匀沙起动临界流速条件。
2.考虑床沙粗化及隐暴作用的起动流速
通过水槽实验和野外实测，获得非均匀沙部分可动和全部可动条件下的暴露度和粒径关系的资料。根据对这些资料的分析，床沙暴露度的定义如图9-6所示。
全部可动时
其中
部分可动时
式中:ei是粒径为Di的颗粒的暴露高度;ΔPi为i 粒径组所占床沙百分比;N、M 分别为全部床沙的分级数和Di＜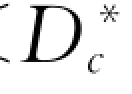
的分级数;DA为床沙代表粒径;
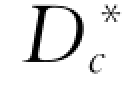为床沙调整的最大可动粒径;A 为床沙位置特征参数。
A 值越大，粗化程度越强(上游泥沙补给不足)，细颗粒泥沙受到的荫蔽作用也越强。A 是表征床沙位置关系和上游泥沙补给条件的重要特征参数。
非均匀沙的起动流速，可在均匀沙起动流速的基础上，引入粗细颗粒间相互影响的参数后获得。对于均匀沙粗细颗粒的起动流速，分别有许多计算公式。华国祥于1964年提出了一种均匀沙起动流速计算方法。通过受力分析并采用指数流速公式，可以获得粗颗粒和细颗粒的起动流速表达式的统一形式:
式中:K1、K2为待定系数。由实际资料适线，得K1=1.15，K2=10，则
图9-7点绘了式 (9-10)和实验资料的对比，说明起动流速公式 (9-10)是可用的。
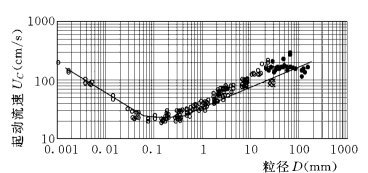
图9-7 起动流速公式与实测资料的对比 (水深H≈0.15m)
与均匀沙相比较，细颗粒 (Di＜DA)位于平均床面之下¯ei，要达到和均匀沙时同样的起动，则Di(Di＜DA)粒径的颗粒的粒径需要加大到Di=¯ei-Di=A(DA-Di)，才能使其顶部达到平均床面，与均匀沙时有同等的起动条件。因此，非均匀床沙中细颗粒泥沙与均匀沙时相比的等效粒径为
对于粗颗粒泥沙 (Di＞DA)，位于平均床面以上ei，要达到与均匀沙时同样的起动，则Di粒径的颗粒需要减小至Di-A(Di-DA)=Di+A(DA-Di)，才能使其顶部位于平均床面上，与均匀沙时有同样的临界起动条件。而对于Di＞
的颗粒的等效粒径，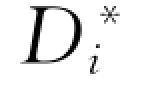
=Di+A(DA-
)。
综上所述，非均匀沙等效粒径可表达为
式(9-13)就是考虑粗细颗粒间隐暴作用的非均匀沙分组起动流速公式。
9.2.2.2 宽级配沙卵石推移质输移特性
山区卵石滩航道整治过程中，河床会发生冲刷使床沙逐渐粗化，降低河道的输沙能力。因此，在一定的边界条件下，可进行水沙调节，使水沙相匹配，恢复河道的输沙能力，让河道朝有利的方向发展，减少减缓河道的淤积。可以用例子来简要说明粗化细化对输沙能力的影响:在水槽上铺一定厚度的粗细泥沙，施放清水进行冲刷使其完全粗化稳定，此时粗化程度达到最大，输沙率为零。然后，取下粗化层级配，并按此级配重新配沙并铺在水槽中，施放与前述粗化稳定时同样的水流，则输沙率显然不为零，粗化程度则为零。两者的主要差异在于粗化细化程度不一样，前者粗化程度最高，后者则反之。这就反映出，粗化程度的不同导致不同的输沙强度 (或输沙率)。反过来讲，作为粗化过程的反过程——细化过程，在水流相同条件下，细化程度越大，则输沙强度亦较高。冲刷粗化过程的输沙强度明显小于淤积 (细化过程)的挟沙强度。另一方面，粗化细化是一连续过程，冲刷中有着不同的粗化程度，细化中亦存在不同的细化程度，不同程度的粗化细化，其输沙规律也不一样。
床沙粗化伴随河床床面粗糙加大，伴随细化而来的是床面光滑。粗化过程的最终状况是粗化稳定层的形成，此时粗化程度系数亦定义为1。当然粗化也许不形成粗化稳定层。粗化开始时的粗化程度则认为是零。细化过程作为粗化过程(冲刷)的逆过程，淤积细化开始时细化程度为零。
非均匀沙颗粒的运动，存在着大小颗粒间的相互影响，造成大小颗粒间相互影响的原因是非均匀沙颗粒在床面上的位置关系。颗粒处在床面上的位置不同，则颗粒所受水流力也不同，从颗粒的受力大小，颗粒的跳跃运动及其实际测量等方面考虑，引入如图9-6所示的暴露高度ei的概念。
由图9-6可见，暴露高度就是基线0—0到颗粒顶点的竖向距离。基线0—0为床面表层泥沙平均暴露高度面，即平均床面。这样，位于平均床面上的颗粒的暴露高度也刚好为零;暴露高度也可是正，也可为负，取值为正时表示突起于平均床面之上，为负时表示低于平均床面。
由图9-6可知，这种暴露高度，不仅反映了某一颗泥沙在床面上的位置，也反映了与该颗泥沙相邻颗粒在床面上的位置，相邻颗粒间的相对位置关系正好反映了非均匀沙大小颗粒间的相互影响关系，因而反映了非均匀沙颗粒在床面上的位置特性。下面介绍暴露高度的实测方法及暴露高度与颗粒大小的关系。
暴露高度的实测在活动玻璃水槽进行，水槽长20m，宽40cm，高50cm。实测时，用一块10cm×10cm 的小板，用一无尖测针与板面垂直连接，将测针架固定在所测断面上，在板面上涂一层薄薄的白乳胶，将测针连同小板安装在测针架上，调节测针向下移动，至床面起最高部分颗粒时，记录测针读数，并将板面上所粘泥沙洗下，烘干、筛分出各级泥沙的重量，这便是这一测针读数下暴露颗粒的重量;重复以上过程，直至测完表层颗粒为止，就可以得到不同测针读数下各级泥沙的重量。同时，在岷江都江堰河段进行了床面泥沙颗粒的暴露高度的测量。
在非均匀沙中，从平均角度来讲，大颗粒位于平均床面上，其暴露高度大于零，受到暴露，细颗粒泥沙暴露高度小于零，故小颗粒输沙受到隐蔽。从实测可知，刚好位于平均床面，即暴露度刚好为零的颗粒也恰好是输沙刚好不受隐蔽的颗粒，同时也不受暴露。这种暴露高度为零的颗粒的粒径称为非均匀沙的代表粒径，以DA表示。
非均匀沙大小颗粒在床面上的暴露高度有着它自身的规律。用上述方法对床面颗粒暴露高度进行实测，由多组实测资料的结果表明:暴露高度和床沙粒径间存在两类典型的关系，如图9-8所示。
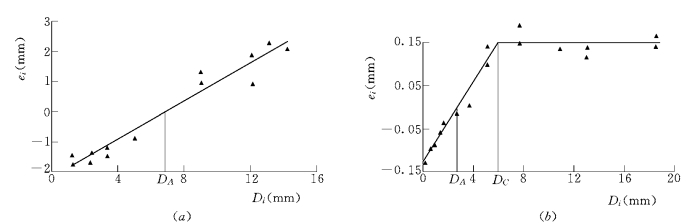
图9-8 床沙暴露高度与粒径的关系
(a)床沙全动时;(b)床沙部分可动时
图9-8 (a)所对应的是床沙全动时的暴露高度和粒径的关系，由图可知，暴露高度随粒径线性增长，表达式如式(9-4)～式(9-6)。
式(9-4)中的常数A 是表征床面粗糙程度的参数，A 值愈大，则大小颗粒的暴露高度相差亦大，床面愈粗糙。反之，A 值愈小，大小颗粒的暴露高度相差亦小，床面也就愈平滑。A 值是反映各条河道的床面粗糙程度的参数，对不同河道亦不同，这也正是各条河道输沙特性不尽相同的原因之一。从都江堰水文站及青衣江梯子岩水文站资料可推得这两处河道的A 值在0.3～0.5间变化。
参数A 越大，床面粗化程度也大，A 趋于零时，床沙趋于刚发生粗化。因此，A 间接地表征了床沙粗化程度的大小，曾用梯子岩、都江堰实测资料，反求两条河流的A 值在0.3～0.5之间，说明两条河流均处在粗化过程中。事实上，河流一般均处在粗化过程中的某一粗化程度(或细化程度)，不会达到完全粗化状况。床沙位置特征参数A 一般不会达到1，而会在某一较大值时粗化稳定层趋于完成，此时床沙位置特征参数为Am;定义此时的粗化程度为1。因此，可以简化认为粗化程度:
虽然这是从粗颗粒泥沙测量得到，对于细颗粒床河也有类似特点。关于细化过程中的细化程度有待进一步研究。
在引入粗化程度概念后，可以考虑粗化程度对输沙能力的影响。由于Einstein公式应用广泛，可以引入粗化程度参数修正、导出宽级配非均匀卵石推移质输沙率公式如下:
其中
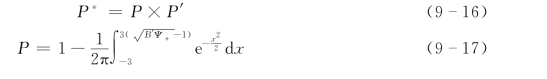
式中:P 为起动概率。
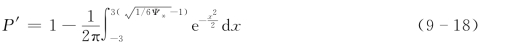
式中:P′为跃过下游颗粒的概率。
式中:gbi为i径组推移质输沙率;Pi为i粒径组床百分数。
由实验资料适线得:B′=0.046，A*=1.6。
粗化程度影响参数
上述宽级配推移质输沙率公式与其他公式的不同之处，在于引入了粗化参数A。不同的A 值，隐蔽参数不同，这正反映出不同河流卵石推移质输沙规律不尽相同的事实。
粗化程度对宽级配推移质输沙率的影响主要表现在对于隐蔽参数的影响，不同粗化程度的隐蔽参数ζ不一样，如图9-9所示。图中点绘了床沙位置特征参数A=0.1，0.2，0.4和0.6时的隐蔽参数ζ的计算值和实验资料对比的情况，关系符合尚好。说明隐蔽参数ζ随粗化程度变化而变化。
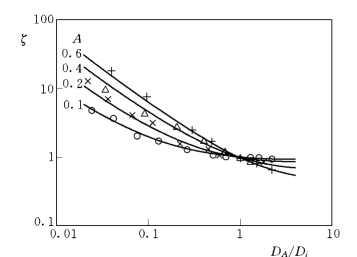
图9-9 隐蔽参数和粗化程度关系
为了便于计算，在原有公式和资料的基础上回归得到非均匀沙推移质输沙率公式如下:
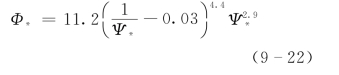
式中:
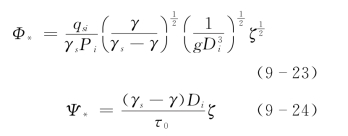
式中:τ0=γH J，为河床床面切力;γs，γ，Di，H 和J 分别为床沙比重，水比重，i粒径组粒径，水深和能坡;Pi为床沙中i粒径组床沙所占比例;ζ为非均匀沙推移质输沙隐蔽系数，由下式决定:
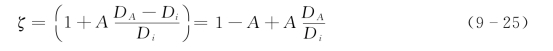
式中:DA为代表粒径:
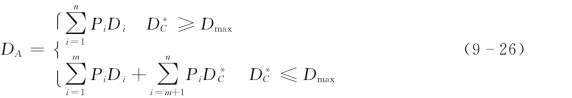
式中: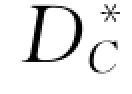
为最大起动粒径;Dmax，m 和n 分别为床沙最大粒径，小于
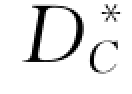的分组数和总的分组数;A 为床沙位置特征参数，是反映床面粗糙程度的参数，取值为0～1，在西南地区河流中取值为0.3～0.5。
粗化细化过程存在不同的粗化细化程度，其输沙能力各异。粗化细化对输沙能力影响很大，而各条河道的粗化程度不尽相同，因而输沙能力相差很大;同一河段的不同时期，粗化细化也不相同，输沙能力也不相同，实际计算中应特别注意。
有关泥沙研究进展的文章
- 详细阅读
-
观测推移质运动的三维测速方法及其应用研究详细阅读
现有的三维测速多数是对水流结构及悬移质的测量，对推移质运动的观测则非常少见。对此Muste et al. 对毫米量级的粗颗粒泥沙运动进行了试验研究，所得的两相速度差在纵向和垂向上基本都与ω在同一量级。刘大有等将近壁颗粒的脉动划分为两种形式，即除了跟随水流的湍流脉动外，还存在颗粒跃移与壁面碰撞等方式引起的非湍流脉动。Muste et al. 对粗颗粒泥沙的观测也表明，近壁区流体的垂向脉动强度要小于颗粒脉动。......
2023-06-22
-
推移质颗粒三维运动的平均特性分析详细阅读
采用三维粒子示踪测速技术，通过分别改变示踪粒子的粒径、比重以及水力比降等条件，观测了10种不同水沙条件下推移质颗粒的三维运动。对推移质颗粒的平均运动规律进行统计分析，探讨粒径、比重及水力比降对推移质运动速度的影响，并分别根据Einstein和Bagnold的研究方法从实测资料得出推移质纵向平均速度的表达式。由图1-12可知，随着坡降的增加，推移质颗粒的速度明显增大，颗粒与水流的相对运动速度减小。......
2023-06-22
- 详细阅读
-
推移质起动概率分析详细阅读
表面淬火只对表面层进行加热，所以淬火后变形不大，对于精度要求不是很高的齿轮常不需要磨齿。冲击载荷很大时应采用渗碳淬火。渗碳层厚度一般取齿根厚度的 10%～15%，但不大于1.5 mm。但由于硬化层很薄，承载能力不及渗碳淬火齿轮。由于铸铁较脆，为避免载荷集中而引起的齿端局部断裂，齿宽一般应取小些。表6.4常用齿轮材料及其力学特性图3.1-32起动概率随相对水流强度参数的变化趋势......
2023-06-21
-
推导推移质公式详细阅读
推移质公式推求当运动泥沙与床面泥沙的交换达到平衡，即单位时间内自单位床面上冲刷外移的泥沙数量正好与沉积下来的泥沙数量保持相等时的输沙率。Einstein 经过推导得出在单位面积上将有重量为的泥沙被冲刷外移，其中A1、A2为与泥沙颗粒形状有关的系数。图1-2修正的Einstein公式与实测资料的对比图1-2修正的Einstein公式与实测资料的对比......
2023-06-22
-
桥涵水文学-推移质输沙率详细阅读
起动流速是推移质运动产生的条件，沙波运动是推移质运动的主要形式，而推移质运动的强烈程度则用推移质输沙率来表示。推移质输沙率的大小，对河流的冲刷和淤积有着重要意义。推移质输沙率的计算方法，有几种不同的研究途径。目前我国的桥下一般冲刷中，采用以流速为主要参数的推移质输沙率公式，这种计算方法认为影响推移质输沙率的主要因素是水流的流速。......
2023-11-20
-
推移质多年平均输沙量的估计方法详细阅读
但目前由于实测推移质资料短缺，使推移质输沙量直接计算有一定难度，现有估算方法如下。若具有多年推移质资料时，其算术平均值即为多年平均推移质年输沙量。——多年平均流量，m3/s；J——原河道的平均比降，‰；Ms——悬移质输沙量模数，t/km2。......
2023-06-21
相关推荐