图8.2-1三峡水库各研究方案不同区间下泄流量年平均出现天数泥沙冲淤影响计算采用第5章一维非恒定流不平衡输沙水流泥沙数学模型研究成果。表8.2-5三峡水库泥沙冲淤计算方案8.2.3.1 水库泥沙淤积影响不同汛限水位方案运用50年,水库淤积量计算结果见表8.2-6和图8.2-2。......
2023-06-21
8.4.3.1 泥沙对硝酸铵扩散的影响
图8-12比较了0.5m/s流速下硝酸铵在清水中和含沙量分别为5kg/m3、23.5kg/m3的含沙水流中扩散的试验结果。从图8-12可以看到,随着含沙量的增大,硝酸铵的扩散速度并没有明显的规律性变化。
8.4.3.2 含沙量对沙掺混的影响
图8-13比较了不同含沙量的水流中沙掺混试验的结果。从图8-13中看到,在相同的流速下,沙掺混速度与水流含沙量关系不明显。
8.4.3.3 泥沙对铜扩散的影响
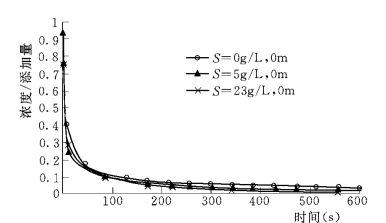
图8-12 相同流速 (0.5m/s)下硝酸铵在清水和含沙水流中扩散的比较

图8-13 相同流速 (0.5m/s)不同含沙量水流中沙掺混的比较
图8-14、图8-15比较了相同流速下铜在清水及不同含沙量的水流中的扩散过程,从图中看不到含沙量对铜的扩散速度有统一的规律性的影响,而且清水、不同含沙量的水流中的扩散速度的差别也比较小,因此可以认为在试验含沙量范围内,铜(总量)在清水中和不同含沙量水流中的扩散速度是相近的。
含沙水流中铜的迁移扩散是由三个同时进行的过程耦合而成的,即溶解态铜的迁移扩散,沙对铜的吸附解吸反应,以及吸附态铜随沙的掺混。
根据前面的试验,在本试验含沙量范围内,沙的存在不影响硝酸铵的迁移扩散。由此可以推测,含沙水流中溶解态铜的迁移扩散规律与清水中铜的迁移扩散是相近的。被吸附的铜随吸附沙粒在水中的掺混过程而发生迁移扩散,前面的分析已表明沙掺混过程的速度受水流含沙量影响不明显,而且和铜在清水中的扩散速度没有显著差别,因此,被吸附的铜的迁移扩散和溶解态铜在清水中的迁移扩散速度也是相似的。
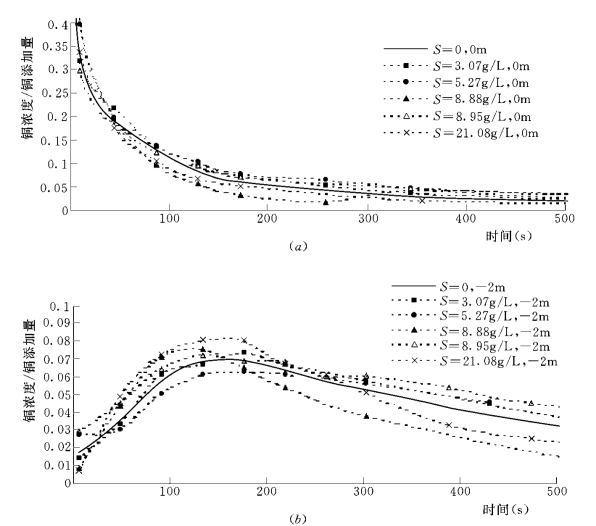
图8-14 相同流速 (0.5m/s)不同含沙量水流中铜扩散的比较
这样,溶解态铜和吸附态铜在水中迁移扩散的速度都和铜在清水中的迁移扩散速度相近,因而总铜的迁移扩散速度必然和清水中铜的迁移扩散速度相近,而且不受铜在两相间分配比例的影响,也就是说,在不同的含沙量(本试验含沙量范围内)和吸附过程下,总铜的迁移扩散速度都是相似的。
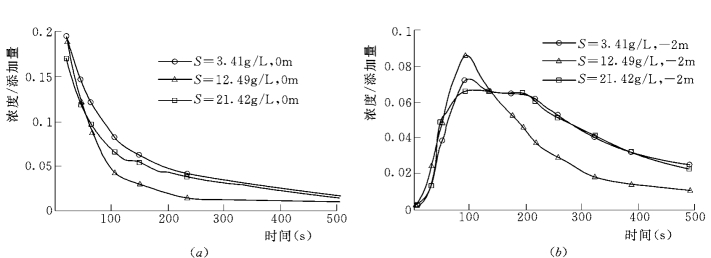
图8-15 相同流速 (1.0m/s)不同含沙量水流中铜扩散的比较
8.4.3.4 挟沙水流中铜扩散的数值计算和分析
Taylor(1953,1954)研究了圆管层流和紊流中瞬时点源下游的纵向离散问题,得到了与试验资料基本一致的理论成果,为后来的一维纵向离散的研究打下了基础。根据Taylor的讨论,在以断面平均流速U 下移的运动坐标系中,圆管中的纵向离散可用下式描述

式中 K 称为综合扩散系数或混合系数(mixing coefficient)
![]()
Taylor推导得出的纵向离散系数(弥散系数)、紊动扩散系数和综合扩散系数分别为

式中:r0为圆管半径;u*为摩阻流速。
从式中可见Dt≪DL,因此实际计算中经常忽略Dt,以离散为主。根据式 (8-15)和摩阻流速公式,结合本实验的具体条件,可以把混合系数描述为下面的形式
![]()
1.铜迁移扩散中的总量变化过程
为了得到本实验条件下混合系数的数值,采用以水流平均流速U 向下游移动的运动坐标系,以式(8-11)为基础进行循环管道中一维离散的数值计算。
把整个管道划分为等长的m+1段,分别标记为L0,L1,…,Ln,每段长为Δx,整个计算时段划分为等长的T 段,分别记为T0,T1,…,TT,每段长为Δt,Li管段在Tn时段的扩散质浓度记为Cin。将中心差显示应用于式(8-11),得

计算中共有Q、U、α和Δx 四个参数。注意到计算中用的是运动坐标系,U 只用于和α 一起计算混合系数K;Q 的取值不影响扩散规律;Δx 的取值并不影响结果只要直观上合理即可。因此,计算中Q 一律取1mg,以与作了归一化的实验数据相对应,Δx 一律取0.05m,这样,真正有意义的参数只有U 和α,特别是α。
计算了流速分别为0.25m/s、0.5m/s、1.0m/s、2.0m/s时的离散,在每个流速下α均取10.1、20.2、30.3、40.4、50.5五个值,即Taylor的理论推算值10.1的1~5倍,把这些流速下的扩散试验实测值与计算值相比较,见图8-16~图8-18。
从以上各图可以得到以下几点认识:
(1)实测数据与计算结果基本吻合。说明本试验中所研究的问题基本可看作一维恒定均匀流中的离散问题,上面的计算方法是可信的。
(2)0m 线实测数据与计算结果的吻合程度稍好于-2m 线。-2m 线实测值与计算值的分歧突出表现在扩散初期,实测值的增长速度明显慢于计算值。
(3)硝酸铵和铜在清水和浑水中扩散的试验中,α一般在20.2~30.3之间;沙在清水中扩散的试验中,α大致在40.4~50.5之间;沙在含沙水流中掺混的试验中,α 大致在20.2~30.3之间。
(4)在上面某些图中,实测的扩散过程线陆续切过计算出的过程线,有的偏离还比较大,但这种现象并无统一的特征,其产生可能和多种因素有关,可能反映了混合系数在扩散发展的不同阶段有变化,也可能是由于试验中的偶然误差、系统误差,以及数值分析中的问题等原因造成的。
(5)在硝酸铵的四种流速试验数据中,流速低的与计算结果吻合好,流速越高,实测值与计算值吻合程度越差,而且流速为1.0m/s和2.0m/s的试验数据似乎与物质守恒原理有较大偏差。但试验中并无严重滴漏问题,而且采样之外的扩散质偶然损失也和试验流速无关。据计算,采样造成的管道中扩散质总量损失,在14次有效试验中,有9 次在10%以内,其余5次在10%~17%之间,而流速为1.0m/s和2.0m/s的硝酸铵扩散试验的采样损失均在10%以内。因此,上述现象似乎与管道中扩散质总量不守恒无关,其原因有待进一步分析。
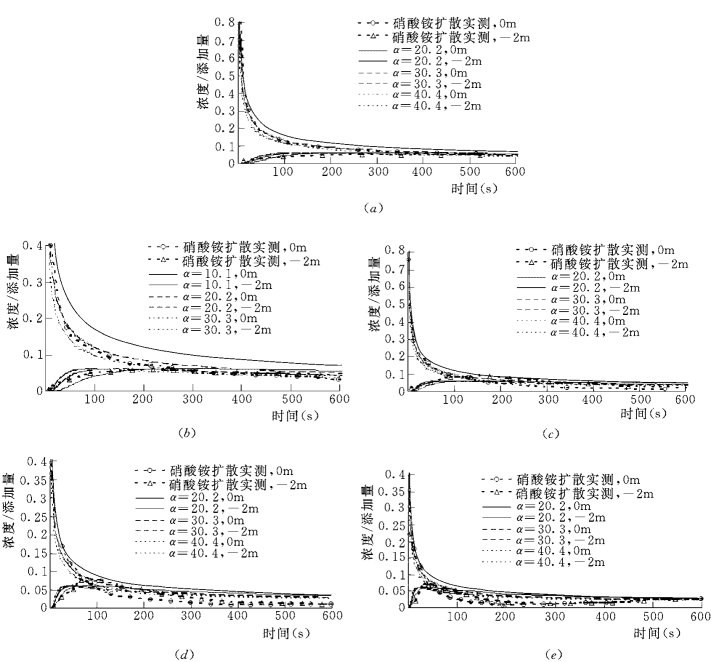
图8-16 硝酸铵扩散实测数据与数值计算结果的比较
(a)U=0.25m/s,清水;(b)U=0.5m/s,清水;(c)U=0.5m/s,含沙水流,S=23g/L;(d)U=1.0m/s,清水;(e)U=2.0m/s,清水
2.铜迁移扩散中的液相浓度变化过程
在天然河流中,重金属主要吸附在悬浮物和底泥上,以溶解态存在于水中的量很少。但溶解态重金属恰是生物活性大、危害最严重的部分,理所当然地受到特别关注。
如前所述,含沙水流铜扩散试验中的三个主要过程是液相迁移、吸附解吸反应和吸附相迁移。液相铜浓度变化过程作为整体过程的一部分,受到其他两个过程的直接影响。
已知液相铜的扩散和吸附相铜的扩散机理如式 (8-11)所示,吸附解吸反应方程如式(8-2)所示,若以c,N 分别表示液相铜浓度和泥沙的吸附量,则有
![]()
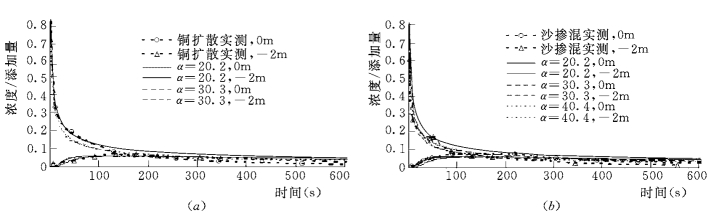
图8-17 沙扩散和沙掺混实测数据与数值计算结果的比较
(a)U=0.5m/s,清水;(b)U=0.5m/s,含沙水流

图8-18 铜扩散实测数据与数值计算结果的比较
(a)U=0.5m/s,清水;(b)U=0.5m/s,含沙水流,S=21.1g/L;(c)U=1.0m/s,含沙水流,S=21.4g/L
![]()
式中:K1和K2分别是液相铜扩散和沙掺混的混合系数,这里取K1=K2。
类似地,对流速0.5m/s,含沙量分别为2.18g/L、4.74g/L、9.53g/L、18.70g/L四种情况计算了液相铜浓度的变化过程。式(8-19)、式(8-20)中参数b、k1、k2取值参照表8-10。并取
![]()
图8-19是四种含沙量水流中液相铜变化过程的计算结果。从图8-19中看到,不同含沙量的水流中,液相铜浓度的变化过程差异不很大,而且不同含沙量水流中相同时间相同位置的液相铜浓度并不是随着含沙量的增大而定向变化的。其主要原因可能是由于所用的计算参数中吸附速率系数随含沙量增大而减小。由于计算结果受到k1和k2取值的巨大影响,如果不同含沙量下k1和k2的取值与本试验的测量值呈现不同的规律,含沙量对计算结果的影响就可能有很不同的表现。

图8-19 含沙水流中液相铜浓度变化过程的计算结果
图8-20比较了含沙水流中总铜的实测值与液相铜的计算值,二者显示出明显的差异:在扩散初期,液相铜和总铜的变化过程相近,当扩散进行了一段时间以后,液相铜浓度迅速降低,明显低于水沙两相铜的总浓度。这是因为扩散初期扩散质纵向浓度梯度大,扩散迅速,吸附作用相对慢得多,总铜中吸附态铜所占比例较小。当扩散发展了一定时间,纵向浓度梯度已大大降低,扩散速度变慢,吸附反应的速度相对来讲不可忽视,吸附作用造成的液相浓度降低就逐渐显现出来。根据图8-20,在扩散进行了550s时,液相铜浓度(计算值)约占总铜浓度(实测值)的1/8。
计算了与图8-20同一过程中0m 点和-2m 点的液相铜浓度占总铜浓度的百分比(以下记为θ),示于图8-21。图8-21清楚地显示了θ从接近1逐渐下降,直到趋于稳定的过程,而且对水流中不同位置,θ几乎完全相同。t=1000s时θ=0.03434。
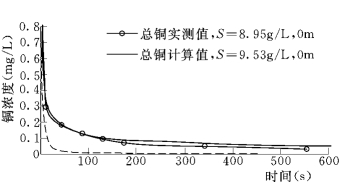
图8-20 含沙水流中总铜实测值、计算值及液相铜计算值的比较 (U=0.5m/s)
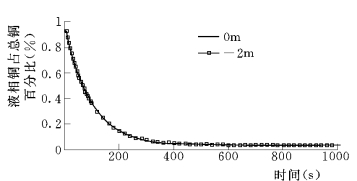
图8-21 含沙水流中液相铜占总铜百分数的变化过程
实际上,图8-21中θ所趋向的最终稳定值可以通过简单的计算得到。因为试验管道封闭,当时间足够长时,可以认为扩散质在管道中已达到均匀分布。分别以S、Q、A、L、Cl和Ct表示含沙量、加入的扩散质总量、水流断面积、管道总长度、 (水流中某一点)液相铜浓度和水沙两相铜总浓度,显然有
![]()
由于时间足够长,铜在水沙之间已建立平衡,由式(8-1)得
![]()
联立以上两式,并把各参数值代入,得到θ=0.03435。
现在看无限长直管一维恒定均匀流中的离散。仍在符合本试验结果的“沙掺混与液相铜离散的混合系数相同”这种简单情况下,将式(8-19)、式(8-20)中的K1和K2统一用K 表示,式(8-19)+式(8-20)×S,得

因此有解析解
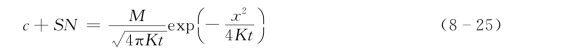
把上式右边记为Ct(x,t)。因为时间足够长,可认为铜在水沙间已建立平衡,根据式(8-1)有
![]()
将式(8-26)代入式(8-25)解得
![]()
于是

由于
![]()
对上式应用罗必达法则,得
![]()
上式可用来计算一维恒定均匀流中重金属迁移扩散较长时间后在水沙两相之间的分配比。上式反映了如下特点:
(1)经过足够长时间,吸附反应达到平衡后,虽然不同位置的Cl、N 和Ct可能各不相同,而且由于流场为一维无限长,各点的Cl、N 和Ct还在继续减小,但水流中各处重金属总量中液相部分所占的比例达到同一个极限值θ。
(2)θ值与极限吸附量b、吸附强度k以及水流含沙量S 有关,其中b和k 基本上是由重金属和沙的本性决定的,S 属于水流中的外部条件。
(3)由式(8-30)容易看到,θ与b、S 成负相关,与k 成正相关,或者说,与解析速率系数k2成正相关,与吸附速率系数k1成负相关。总之,与促进吸附的因素成负相关,与抑制吸附的因素成正相关。
式(8-30)是在一些比较理想化的前提条件下得出的,这些假设条件主要包括:
(1)水流条件可近似看作一维无限长恒定均匀流,含沙量也要求是均匀、稳定的。
(2)泥沙全部悬浮,没有和底泥、边壁的交换,吸附性扩散质初溶解部分外,只被悬移沙所吸附,没有其他源汇项。
(3)沙掺混的混合系数与水中溶质纵向离散过程的混合系数相等或十分相近。
通过对试验数据的定性分析、定量解析和数值计算,在试验的水流条件下和含沙量范围内,得到以下主要结论:
铜的吸附可用Langmuir吸附等温式和吸附反应动力学方程来描述,对试验数据的拟合效果较好;极限饱和吸附量用(非饱和)试验数据拟合似乎不如用饱和吸附试验直接测定来得可靠;本试验中得到极限饱和吸附量和吸附强度基本与泥沙浓度无关,而吸附速率系数和解析速率系数则随泥沙浓度增大而减小。
在本试验水流条件下和含沙量范围内,水沙两相铜总量的迁移扩散规律在清水中及不同含沙量的含沙水流中基本相同,其原因主要是由于本试验中沙掺混速度与水中溶质离散速度相近。
铜在含沙水流中迁移扩散时,溶解态铜浓度的变化规律与水沙两相铜总浓度的变化规律明显不同。如果铜是以溶解态进入水流中的,则在扩散初期,溶解态铜在铜总量中占大部分,溶解态浓度变化过程与总浓度变化过程相近;随着扩散的发展,吸附作用迅速进行,溶解态浓度迅速减少,铜以沙为主要载体进行迁移扩散,表现出含沙水流对重金属污染物的自净作用。
导出了一维恒定均匀流中重金属水沙极限分配比的计算公式,公式表明:重金属污染物在含沙的一维恒定均匀流中迁移扩散足够时间后,水流中各处的重金属水沙两相分配比达到同一个稳定值,该值由泥沙和重金属的吸附特性参数和水流含沙量决定。
(本章作者:倪晋仁 张泽蒲)
有关泥沙研究进展的文章

图8.2-1三峡水库各研究方案不同区间下泄流量年平均出现天数泥沙冲淤影响计算采用第5章一维非恒定流不平衡输沙水流泥沙数学模型研究成果。表8.2-5三峡水库泥沙冲淤计算方案8.2.3.1 水库泥沙淤积影响不同汛限水位方案运用50年,水库淤积量计算结果见表8.2-6和图8.2-2。......
2023-06-21

图14.25葛洲坝坝区河段示意图14.5.4.1对水力条件的影响水库蓄水后,坝区水力条件将发生明显变化,主要体现在水面比降变缓、流速减小。图14.261998年、2005年庙河断面流量—输沙率关系图14.5.4.3对泥沙冲淤特性的影响进入水库的洪水过程一般是非恒定流,使坝前流量、含沙量等发生变化,对坝区河段泥沙冲淤变化也产生了一定影响。......
2023-08-23

从图6.46可看出,点火位置布置方案1和2的电热塞处于燃烧室前部的单向流区,方案3的电热塞处于燃烧室前部的滚流区。图6.46不同电热塞布置方案的流场图6.47和图6.48给出了方案2和方案3燃烧过程中的温度场变化过程,方案1的温度场已经在图6.41和图6.43中给出。三种火花塞布置方案的燃烧传播已有明显的不同,随着燃烧过程的进行,火焰从燃烧室前侧向后侧迅速发展。......
2023-06-23

在火花塞布置方案采用方案1,原始点火提前角60°的基础上,对比分析了不同点火提前角对缸内燃烧过程的影响。图6.51所示分别为点火提前角为40°、50°时,在上止点前20°时的温度场和NO浓度场。即随着点火提前角的提前,在上止点时剩余的未燃混合气减少。从图6.53可以看出,随着点火提前角的增大,火焰发展期和快速燃烧期的相位不断提前。从图6.54缸内压力曲线可看出,点火提前角为上止点前60°时的压力峰值最大。......
2023-06-23

如图2-5中,工件旋转一周的时间,刀具正好从位置Ⅰ移到Ⅱ,切下Ⅰ与Ⅱ之间的工件材料层,四边形ABCD称为切削层公称横截面积。切削层实际横截面积是四边形ABCE,AED为残留在已加工表面上的横截面积,它直接影响已加工表面的表面粗糙度。图2-5切削层参数切削层形状、尺寸直接影响着切削过程的变形、刀具承受的负荷以及刀具的磨损。......
2023-07-01

图2-1床沙质含沙量与无量纲单位水流功率参数的关系为了说明大水深河流和水深较小的实验室水槽中输沙能力的不同,图2-1点绘了床沙质含沙量与无量纲的单位水流功率参数的关系。小水深水槽试验和大水深河流雷诺数的差别达到两个数量级,这种差别必然会影响到水流阻力和与之相关的泥沙输移过程。图2-3的结果再次说明,由于实验室水槽的水深变化范围有限,依据实验室水槽资料建立的输沙关系,不能够代表大河流的输沙关系。......
2023-06-22

产品的可装配性与产品的结构要素密切相关,主要包括材料、形状、连接方式、精度等。根据产品的装配工艺过程,可以对不同产品的设计对最终的装配工艺的影响进行分析。不同的连接方法一般还要求采用特定的装配工装和装配工具完成最终的装配,也对装配的工艺安排有一定的影响。......
2023-11-22
相关推荐