铜在水沙两相间的分配随着扩散的进行和时间的推移而变化，其主要控制因素就是沙对铜的吸附、解吸反应速率，以及反应速率与扩散速度的对比情况。因此需要研究试验条件下铜的吸附速率，并与扩散速度进行比较。对于本试验所关注的问题而言这也是合适的。试验中振荡一定时间后迅速离心，测定液相铜浓度，并计算相应的吸附量。表8-8铜吸附速率实验的实验条件......
2023-06-22
铜吸附速率实验结果和分析
【摘要】：图8-4不同含沙量下铜的吸附过程曲线表8-9铜吸附实验的实验条件和实验结果图8-4不同含沙量下铜的吸附过程曲线表8-9铜吸附实验的实验条件和实验结果从表8-9中看到，在铜初始浓度相同的情况下，反应进行相同时间后的相对吸附率随含沙量的增大而增大。黄委会进行了粒度为0.01～0.025mm 的花园口断面混合悬浮物对Cu的吸附实验，得到Cu的t1/2是30s。利用Langmuir吸附等温式，对4组吸附实验数据，分别计算其k值，计算结果列于表8-10。
实验得到4个不同反应时间的液相铜浓度和泥沙铜吸附量，吸附过程如图8-4所示。根据图中各曲线，可以认为实验结束时已达到吸附平衡，计算了反应进行不同时间铜的相对吸附率(吸附量与平衡吸附量之比)，与其他实验数据一同列于表8-9。
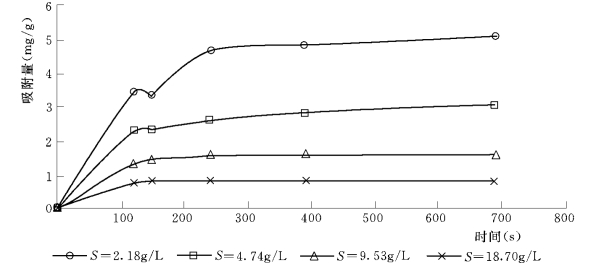
图8-4 不同含沙量下铜的吸附过程曲线
表8-9 铜吸附实验的实验条件和实验结果
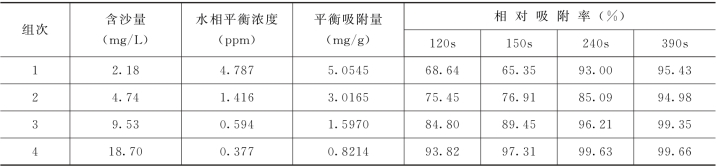
从表8-9中看到，在铜初始浓度相同的情况下，反应进行相同时间后的相对吸附率随含沙量的增大而增大。在实验含沙量范围内，Cu达到50%相对吸附的时间t1/2在100s以内。因为试验取样时间不够密集，还不能对t1/2作出更准确的估计。黄委会进行了粒度为0.01～0.025mm 的花园口断面混合悬浮物对Cu的吸附实验，得到Cu的t1/2是30s。因此，与本节流动试验中的扩散过程相比，吸附过程是很快的，吸附和扩散两个过程同时进行，对铜的迁移都产生重要影响。
下面利用吸附模型方程对试验数据做进一步的定量分析。
描述河流泥沙对重金属污染物的吸附常用Langmuir型、Freundlich型及Henry型等温吸附模型方程。这些吸附模型方程主要包括吸附等温式(线)和吸附(反应)动力学方程。吸附等温式表达一定温度下单位质量泥沙平衡吸附量和水相平衡浓度的关系，描述的是一种平衡状态，根据这一关系可以绘出吸附等温线。吸附动力学方程表达吸附速率与液相重金属离子浓度、泥沙吸附量等影响因素之间的关系，描述的是一种瞬时状态。
上述三种模型都已得到广泛应用但各自的假设条件和适用对象有所不同。由于Langmuir吸附等温线是根据单分子层吸附理论导出的，能较好地适应各种浓度，而且式中每一项都有明确的物理意义，因而已被广泛应用于土壤对溶质吸附和河流泥沙对重金属污染物吸附中。黄岁梁(张玉清等，1987)通过实验研究，认为Langmuir型吸附模型方程能适应较宽的重金属浓度范围 (包括高含量重金属浓度范围)，适于描述泥沙对重金属的吸附。
Langmuir吸附模型方程的吸附等温式和吸附动力学方程分别如下:
式中:N∞和c∞分别为单位质量泥沙的平衡吸附量和水相平衡浓度;N 为单位质量泥沙的瞬时吸附量;c为水相瞬时浓度;b为吸附达到饱和时的最大极限吸附量;k1和k2分别为吸附速率系数和解吸速率系数;k值相当于吸附量达到饱和吸附量的一半时的水相平衡浓度，也称为吸附强度，实际上等于解吸与吸附速率系数之比 (k =k2/k1);t为时间。N∞，N 和b 单位是mg/g，c∞和c单位是mg/L (ppm)，k1单位是1/ (ppm·s)，k2单位是1/s，t单位是s。
一般情况下的泥沙吸附重金属反应过程可用下面一组方程描述:
(1)Langmuir吸附动力学方程，即式(8-2)。
(2)反应器内质量守恒方程
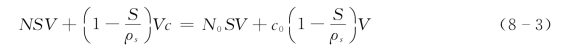
式中:ρs为泥沙密度;V 为容器容积。
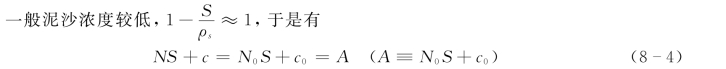
式中:S 为含沙量，g/L;N0和c0分别是泥沙初始吸附量和水相初始浓度。
(3)初始条件
黄岁梁导出N0=0条件下吸附过程中任一时刻泥沙吸附量为
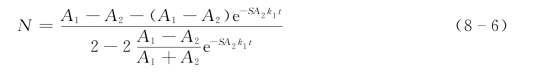
式中
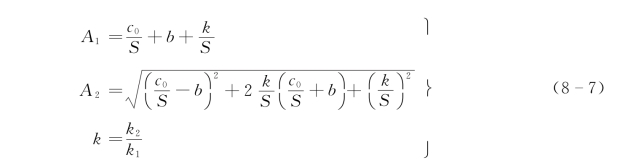
根据上文所述，试验中制备的示踪沙均已饱和吸附了铜，根据对示踪沙含铜量的测定，试验用沙对铜的饱和吸附量b=18.0176mg/g。利用Langmuir吸附等温式，对4组吸附实验数据，分别计算其k值，计算结果列于表8-10。
确定了b和k 之后，对于4组吸附实验中的每一组，式(8-6)中的A1和A2都是定值，泥沙吸附量N 是吸附速率系数k1和反应时间t的函数。把式(8-6)变形为
令上式左边为y，则y 与t成正比。将实验数据按上式回归，回归参数k1连同由k=k2/k1计算出的k2列于表8-10，实测的和拟合的吸附过程曲线如图8-5所示。
图8-5 实测的和拟合的吸附过程线
表8-10 吸附等温式和吸附动力学方程回归参数
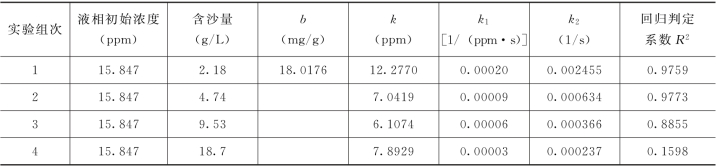
从表8-10中看到，除饱和吸附量b显然是泥沙自身吸附特性，与含沙多少无关外，对不同的含沙量，吸附强度k没有规律性的变化，与黄岁梁“泥沙浓度不影响吸附等温式参数”的实验结论相符。但随着含沙量的增大，k1和k2有减小的趋势，这与黄岁梁“可以认为泥沙浓度对(镉)吸附速率系数k1无影响”的实验结论不同，与金相灿等“(铜吸附反应中)吸附剂浓度增大，吸附速率系数增大”的实验结论相反。
这里最大极限吸附量b是根据饱和吸附了铜的示踪沙的吸附量直接得出的，吸附强度k则是对含沙量不同的各组实验数据利用吸附等温式计算得到，这样，b值为18.0176，k值从6.10到12.28不等。因为不同含沙量下的k 并无趋势性变化，不同含沙量下k 亦可统一取一值。表8-10中四个k的平均值是8.3298。若以式 (8-1)对实验数据回归 (b取定为18.0176)，则得k为10.5257。如果不利用示踪沙的吸附量数据，仅以式 (8-1)拟合实验数据，则得到b和k 值分别为7.2270和2.0562。
当b和k 均通过数据拟合得到时，实验数据与吸附等温式的符合程度最好，这也是理所当然的。但在这样的b、k 值基础上拟合吸附过程曲线，效果则很差。因此，b 和k 的求取仍采用上文所述的做法。值得注意的是，用实验数据拟合得到的b值和饱和实验实测值存在明显差异，其中原因有待进一步讨论。
有关泥沙研究进展的文章
- 详细阅读
-
图像检索实验和结果分析详细阅读
考虑到Corel-10K图像数据库有100个样本类别，共有10 000个样本图像，所以图7-8和图7-9的检索结果展示了本节设计的基于粗略颜色信息和灰度纹理特征相融合的图像检索系统具有良好的检索性能。接下来，给出本节设计的图像检索系统的综合性能评价指标，即查准率和查全率。本节提出的图像检索系统在Corel-10K数据库和Corel-5K数据库上的平均查准率和平均查全率分别如表7-4和表7-5所示。最后，对本节提出的图像检索系统的实时性进行分析。......
2023-06-29
-
实验与实验结果分析详细阅读
之后计算求得该组5个制品减重百分数的平均值xi，作为该组实验的结果。表6-9 实验结果表6-10 实验结果表6-11 实验结果表6-9～表6-11中，每一行为一组实验数据，各因素下为对应的水平号。表6-10～表6-11中实验号5、13、14的实验结果明显小于其他数据，后续数据处理中保留了这些数据，没有作为奇异项处理。图6-32 一个注塑周期的实验数据图所有数据统一在一个时间轴下记录，为后续数据分析提供了便利。......
2023-07-02
-
煤层气储层中CO2和CH4竞争吸附实验分析结详细阅读
5.4.2.2CO2和CH4混合气体的吸附解吸规律研究确定好CO2和CH4两种气体的保留时间和峰比系数之后，本节进行了二氧化碳和甲烷这两种气体在不同的围压下的吸附解吸规律研究。......
2023-11-18
-
实验结果及分析：煤层气吸附解吸规律及压裂液增详细阅读
图5-5甲烷吸附量与孔隙压的关系图图5-6甲烷吸附量与孔隙压的关系图图5-7甲烷吸附量与孔隙压的关系图图5-8甲烷吸附量与孔隙压的关系图本次实验进行了吸附和解吸两个部分。......
2023-11-18
-
切削温度结果分析：车削实验结果分析详细阅读
切削温度计算值与测试值之差相对误差也在5%的允许范围内，见图4-21b。图4-22 车削时切削温度与切削深度、进给量的特征曲面以及切削温度特征曲面等值线图a）切削温度与切削深度、进给量的特征曲面 b）切削温度特征曲面等值线图2.铣削实验结果分析由图4-23a可知，切削温度模型拟合得也较好。......
2023-06-27
-
实验方法及结果分析详细阅读
实验中触头预压力FK保持为25.1N。表6-5为两组实验和仿真的详细结果数据。图6-21为峰值电流为11.3kA时的电流和电动斥力实验波形。表6-5 实验和仿真结果比较在仿真中，表征触头接触情况的参数ξ取值为0.45。而电流峰值为9.0和11.3kA时，对应的触头压力分别为35.4和55.9N。根据式（6-1），可得导电斑点的半径分别为0.158和0.199mm。因此，引入导电桥模型，采用有限元静态分析的方法计算电动斥力是合理的，也是有效的。......
2023-06-15
-
仿真实验及结果分析详细阅读
选取任务数量为64的场景进行仿真，采用静态资源调度算法获得初始调度方案。表9-7新增任务具体参数2）动态调度结果分析采用抢占式快速动态调度算法对动态调度问题进行求解。表9-9不同场景算法调度结果对照表由表9-9可知，抢占式快速动态调度算法的调度结果具有调度收益高、方案变化少和调度速度快的优势。......
2023-07-02
相关推荐