植被侵蚀动力学方程组的研究

2023-06-22 理论教育版权反馈

【摘要】：植被覆盖度抑制降雨侵蚀，而侵蚀又破坏植被，二者的相互作用遵循一定的动力学规律，同时又受到各种生态应力的干扰。在植被—侵蚀动力学中，植被对侵蚀率的控制作用反映在侵蚀率的长期变化上，所以应该采用滑动平均值。

植被覆盖度抑制降雨侵蚀，而侵蚀又破坏植被，二者的相互作用遵循一定的动力学规律，同时又受到各种生态应力的干扰。如果只模拟降雨侵蚀和植被覆盖度的演变过程，可以仅考虑致死应力的作用，因为损伤应力不直接造成植被覆盖度的减少。致死应力如火山爆发、森林砍伐、森林火灾等都是发生在极短的时间内。植被覆盖度因为现有植被的繁殖扩散、遮蔽和涵养水分的作用而增加，由于土壤侵蚀的作用而减少，另外又由于各种生态应力影响而变化，再假设这些生态应力对植被的影响是相互独立的，这样就可以得出植被覆盖度在各种应力作用下的动力学方程:

式中:E 代表侵蚀率，通常取为每年单位面积内泥沙侵蚀量;Kiδ(t0)是发生在t0时的致死生态应力;VR代表人类植树造林对植被覆盖率的影响;a、c为特征参数，参数a 代表着植被涵养水分、繁殖扩散作用下植被的增长率，其值依赖于当地的降雨、环境条件和植物构成，要通过调查资料来确定，参数c代表着侵蚀对植被的破坏作用，相当于每年每平方公里1t的土壤侵蚀量对植被的破坏率，c值的大小依赖于土壤条件和植被的构成，如果土层很薄，少量的侵蚀就会造成植被的严重破坏，c值较大。

应该说明，此处侵蚀率E 是通过长期作用影响植被发育的侵蚀率值，相当于某种滑动平均值。例如取滑动周期为10年，则第10年的E 值等于第6年到第15年的实测侵蚀率的平均值，而第11年的E 值等于第7年到第8年的平均值，以此类推。因此，E 不是实测侵蚀率那样剧烈波动的随机变量。E(t)曲线是反映趋势性演变的光滑曲线。为了方便，仍称E 为侵蚀率。安家沟是黄土高原祖厉河支流东河右岸的一条支沟，位于甘肃省定西县。图7-12是安家沟流域径流量、侵蚀率和侵蚀率10年滑动平均值的实测曲线。可见侵蚀率随径流量波动的脉动变量较大，而滑动平均值则平稳得多，只反映侵蚀率的长期趋势性变化。在植被—侵蚀动力学中，植被对侵蚀率的控制作用反映在侵蚀率的长期变化上，所以应该采用滑动平均值。

pagenumber_ebook=374,pagenumber_book=358

图7-12　黄土高原安家沟流域实测径流量、侵蚀率和侵蚀率10年滑动平均值的变化曲线

土壤侵蚀影响植被发育，反过来又受到植被的影响。式 (7-14)中侵蚀项随植被覆盖度变化而变，因此，必须寻找另一个方程来求解植被覆盖度和侵蚀率两个未知函数。Thornes(1985)对于植被与侵蚀的相互作用过程提出了耦合数学方程组，可以利用其中的侵蚀率变化方程并引进人类活动对侵蚀率的影响加以改造得到:

式中:ER为人类活动对侵蚀率的影响值，包括开矿、修路、耕作等引起的侵蚀率的增加和修梯田、固坡、筑拦沙淤地坝等造成的侵蚀率的减少;b和f 为特征参数，土壤侵蚀松动了土表层，破坏了土壤中的植物根系，会进一步促进侵蚀，参数b代表了这种作用增大的侵蚀率。植被发育稳定土层，限制侵蚀，参数f 代表了植被对侵蚀率的减少率。

将式(7-14)、式(7-15)联立，得到植被—侵蚀动力学方程组(王兆印等，2003b):

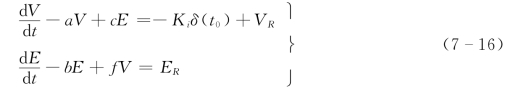
pagenumber_ebook=374,pagenumber_book=358

如果知道t0、ER和VR，且确定了参数a、c、b、f 和Ki，则在生态应力作用下的植被演化就由式(7-16)确定。方程中t的因次为[T]，E 的因次为[M/AT]，参数a 和b 的因次为[1/T]，c的因次为 [A/M]，f 的因次为 [M/AT2];VR的因次为 [1/T]，ER的因次为[M/AT2];其中T 代表时间，A 代表面积，M 代表质量。式中参数a、c、b、f 是气候、降雨量、土壤和地貌的函数，应该根据实测资料并采用试算法来决定。

式(7-16)是非齐次线性微分方程组，可以推导得出理论解:

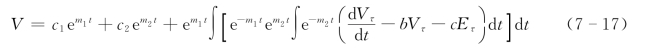
pagenumber_ebook=374,pagenumber_book=358