1977年龙门-利津河段水流模拟计算

为了能精确计算有断面资料部分河道的水沙运动，干流河段不再用上述6.4节介绍的精确扩散波模型，而是采用水动力学法计算。

目前，一维泥沙数学模型因计算速度快，在模拟长河段、长时段的河床变形问题时仍起重要作用，在理论和实践上都比较成熟。考虑在数字流域框架中，模拟的河段范围较长，时间序列也较长，因此，应用于一级河道的水动力学模型采用一维模型，即将所研究河道简单划分为若干个短河段，计算各断面上水沙要素以及冲淤厚度的沿程变化及因时变化情况。一维非恒定泥沙模型中，基本控制方程组包括水流控制方程组和泥沙控制方程组，其中水流控制方程组包括浑水连续方程和运动方程，泥沙控制方程组则包括非平衡悬沙输移方程及河床变形方程(谢鉴衡，1990)。

水流方程组属于一阶拟线性双曲型偏微分方程组，在一般情况下不能得到解析解，需要采取一定的离散方法求其近似解。对一维圣维南方程组的求解方法有特征线方法、差分方法及有限元方法和有限体积方法等。目前在不恒定流的模拟计算中，应用效果比较好的是Preissmann四点偏心隐格式(杨国录，1993)，该格式为一阶精度的隐格式，具有较好的数值稳定性。黄河的洪水期间，一次高含沙洪水过程中含沙量变化迅速，陡涨陡落，常用的迎风格式不能很好地将此类情况考虑进去的，这里采用巨江(1995)提出的方法进行泥沙方程计算。

采用显式格式求解河床变形方程。在计算过程中，分别计算出每个断面、各个子断面的含沙量和挟沙力，从而可以计算其冲淤厚度。考虑到高含沙水流 “淤滩刷槽”的特性，冲刷和淤积具有不同的处理模式:各个子断面都可以有淤积，而只有主槽部位才存在冲刷。

关于基本方程和数值格式可见相关章节及参考文献，这里不再介绍，只对特殊处理做出说明。

6.6.3.1　概况

1977年是典型的枯水丰沙年，三门峡年水量仅307亿m3，年来沙量达20.8亿t，且沙量主要集中在7～8月连续发生的两次高含沙洪水过程，占年沙量的69%。7月洪水主要来自渭河、北洛河、延水等支流的暴雨，龙门站最大实测流量为14500m3/s，实测最大含沙量为690kg/m3，小浪底站最大流量为8100m3/s，最大含沙量为535kg/m3;8月上旬洪水主要来自龙门以上偏关河至秃尾河之间的暴雨，龙门站最大实测流量为13400m3/s，实测最大含沙量为821kg/m3，潼关站整编后洪峰流量15300m3/s，最大含沙量821kg/m3，渭河华县站相应流量还不足100m3/s，其他支流也仅有约300m3/s的流量加入，小浪底最大流量为10100m3/s，最大含沙量高达941kg/m3，花园口站实测到历年最大含沙量809kg/m3。两场高含沙洪水的悬沙组成均较粗，且8月洪水尤为突出。

7～8月两场高含沙洪水在黄河下游河道中均产生了槽冲滩淤现象，由于滩地淤积量远远大于主槽冲刷量，因而整个河道表现为严重淤积，且淤积部位主要发生在高村以上的宽浅游荡性河段，占黄河下游总淤积量的90%以上。洪水过后，边滩淤高，主槽刷深，塑造出相对窄深的断面形态，因此在整个洪水过程中水位变化比较剧烈。

计算范围为中游的龙门站至利津站。因缺少1977年三门峡至小浪底之间的小浪底水库修建之前的实测地形资料，无法进行两站之间河道的水沙计算。经过对比分析两站实测水沙过程可以发现，由于两站距离较短(仅130km)，1977年三门峡站的水沙过程和小浪底的水沙过程基本一致，包括洪峰过程及峰值 (如图6-60和图6-61所示)。可以将需要模拟的河段分为两段:龙门至三门峡河段，长约243km;小浪底至利津河段，长约740km。三门峡至小浪底河段不进行洪水演进计算，假设洪水传播过程保持不变。

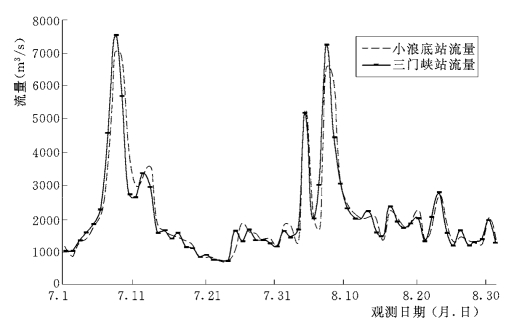
图6-60　1977年7～8月三门峡站与小浪底站实测流量对比图

6.6.3.2　关键问题处理

由于控制方程个数少于未知变量的个数 (即方程组不封闭)，以及黄河下游河床冲淤演变极其复杂，需要引入一些补充关系式来满足方程组求解。

1.边界条件

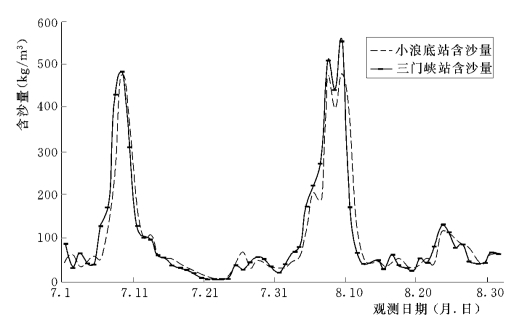
图6-61　1977年7～8月三门峡站与小浪底站实测含沙量对比图

在进行径流演进的一维数值模拟时，由圣维南方程组的特点，须给出问题的初始条件和上下游边界条件，一般来说，上下游的边界条件可由一过程线给出，水流的边界条件是:

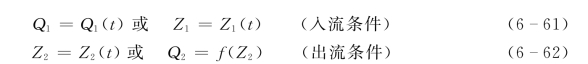
式中:Q1为入流流量过程;Z1为入流水位过程;Q2、Z2分别为出流的流量、水位过程。

上边界给定水流、泥沙及悬沙级配过程，在下边界若为河道则给定水位流量关系，或水位过程，或流量过程，若是水库则需要根据水库的库容曲线和调度方式计算坝前水位。

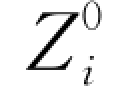各断面的初始条件则根据恒定流计算出初始计算时刻的各项值，并给定相应初始时刻沿程各站的悬沙级配及床沙级配。初始条件对计算结果的影响很大，可能会导致计算结果不收敛。一般情况下，可先进行该河段恒定非均匀流水面线计算，即以某一初始的典型的流量沿程过程，计算出各断面在恒定非均匀流下的水位，以此作为计算的初始水位和流量。当两次迭代值满足给定精度时，此次迭代便可结束，计算则可进入下一个时段。一般而言，其误差在正确边界条件情况下能迅速消失。此外，还包括支流的水、沙及级配过程，以及沿程各站的引水、引沙过程。

2.断面滩槽划分及“二级悬河”处理

在黄河下游段，存在典型的“二级悬河”断面，即主槽平均高程高于滩地平均高程。因此必须划分滩槽，以保证非汛期小水时水流仅在主槽内演进。断面过水情况为:当水位低于平滩水位时，滩区不过水;当水位高于平滩水位时，滩槽均过水。断面划分为3种类型:主槽、嫩滩和高滩。图6-62是黄河下游典型的“二级悬河”断面示意图。

在黄河的下游河段模拟中，若存在“二级悬河”这一特殊地形，则用堰流加水库模式处理。

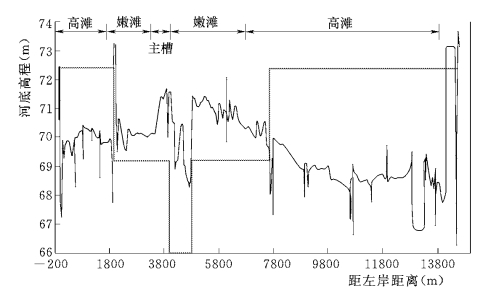
图6-62　黄河典型 “二级悬河”河道横断面示意图

在该河段的“二级悬河”部分，以水箱模式处理，即生产堤 (堰顶高程)外视为水库，在涨水情况下具有存储水量的功能，而在退水情况下，则其储存的水量逐渐恢复运动。即根据堰顶高程、主流水位以及堰外水位，水流的演进情况可分为:没有堰流情况且仅在主槽运动、仅在主槽运动但是有堰流情况以及没有堰流时在全断面运动三种情况，在后两种情况交界的临界点处，需要将滩外存储水量逐渐加入主流。

3.糙率

在一维数学模拟中，通常用曼宁糙率n来表征冲积河道的阻力大小。计算时，只有事先给定糙率，才能进行河道的非恒定流计算。

由于黄河中、下游河道河型变化大，床面形态极为复杂，尤其在下游的游荡河段，河宽变幅较大，而且存在明显的 “二级悬河”情况，沿程各计算断面的形状和面积相差很大，在计算中将糙率作为常数，一般不能满足实际要求。此外，各计算断面的水位、流量变化幅度很大，在同一计算河段用一个不变的糙率不能反映整个流动过程的综合水头损失，也就是说，计算中要使用变糙率，其随河段、水位或流量而变化。但由于在整个需要计算的河道中，各断面的高程总体是沿程下降的，如使糙率随水位变化，在实际中很难操作。因此，通常建立以河段为参数的、糙率与流量的函数关系。

糙率曲线中的流量是流动中若干具有代表性的流量，称为流量级。根据整个河段的实际水流情况，使用了100m3/s、300m3/s、500m3/s、1000m3/s、1500m3/s等19 个流量级。河段则一般选取主要水文测站形成的控制断面。从而使糙率随河段、流量的变化而发生相应的变化。其余断面的阻力，可由各个控制断面的阻力沿程插值求出。

调整和计算糙率的思路是:针对具体的恒定流流量 (流量级)，根据恒定非均匀流方法，反算各计算河段的糙率。实际计算中，整理已有的水文断面资料，根据一维水动力学模型的计算结果，调整这些水文断面在不同流量级下的河道糙率变化曲线，使计算得到的这些水文断面水位—流量关系最能符合各站实测关系。调整完毕后，即可根据当时的流量从已给出的糙率曲线中插值计算应有的糙率，代入圣维南方程组进行河道的非恒定流计算。

另外在计算中，由于下游“二级悬河”(如图6-62所示)等滩槽区别明显的断面的存在，还必须进一步划分滩槽阻力。对于主槽糙率，可由上述已知的流量与糙率关系求得;对于滩地糙率，可按固定值选取，一般取0.035～0.040。此外，遇冲淤变幅很大的情况，床沙级配会有较大改变，根据实际情况对糙率进行微调。

4.下游端为水库泄流控制

若下游端为水库控制，下游的边界条件不能给出水位、流量关系曲线，只能根据水库的库容曲线给出坝前水位，再根据泄流曲线给出下泄流量。

洪水进入水库后形成洪水波运动，是一种具有自由表面的长波，其水力学性质属于明渠渐变非恒定流动。受库周、库底阻力和水库调蓄作用，洪水波形状自入库断面到坝址逐渐坦化，其运动规律可用圣维南方程组来描述。

一种简化处理认为洪水进入水库后，过水断面面积很大，水流流速很小，可近似假定库区流速为零，库面趋近于水平。这样，水库洪水的非恒定流问题可近似地作为恒定流来处理，即略去运动方程，仅考虑坝前水位水平线以下的库容对洪水进行调节，称为“静库容法”。

采用试算法根据水库的库容曲线计算坝前断面的水位和库容，并根据水库泄流曲线可以给出相应的水库泄流的流量过程。试算法是一种概念清楚、适用面广的水库调洪计算方法，尤其是当计算时段不固定和多种泄流设施组合使用时，试算法更具有其灵活性。虽然试算工作量较大，但因有计算机作为计算工具，使得操作计算快捷而准确。

5.其他

泥沙数学模型中悬移质挟沙力是一关键问题。其公式的合理选取，直接影响河床冲淤计算的合理性。天然河道中，影响悬沙挟带能力的有水流、床沙条件。

考虑到可能存在高含沙水流，根据前人经验，这里采用张红武的半经验性挟沙力计算公式。

天然河流中挟带的泥沙往往为非均匀沙，影响非均匀沙的挟沙力的因素一般包括水流、泥沙条件，床沙条件及上游来水来沙条件。这里利用窦国仁(1960)的挟沙力分配模式计算非均匀沙的分组挟沙力。

黄河下游断面极不规则，滩槽水力特性差异较大，若不考虑含沙量在滩地和主槽的区别，用断面平均含沙量计算，将会带来一定不合理性，也不符合实际。参考韦直林等(1997)的悬移质含沙量的横向分布，可由断面平均含沙量推求各子断面平均含沙量。

采用韦直林(1997)的三层床沙级配调整模式对下一时刻各断面的床沙级配进行调整。即将河床分为上、中、下三层，其中，上、中两层保持厚度不变，粒径组成则按照冲淤的不同有不同的处理方法。

在河床变形的计算中，恢复饱和系数的取值，直接影响着河床冲淤量的大小，是悬移质输移计算中一个十分关键的参数，反映了不平衡输沙时，含沙量向水流挟沙力靠近的恢复速度。其值的选取与来水来沙条件有关，也与河床边界有关，是很复杂的参数。但如何确定其具体数值目前尚无定论，不同学者的取值相差很大。这里主要根据率定结果取值。

在计算过程中，分别计算出各个子断面的含沙量和挟沙力，从而可以计算其冲淤厚度。考虑到高含沙水流“淤滩刷槽”的特性，冲刷和淤积具有不同的处理模式，目前简化为:淤积发生在全部断面，冲刷仅发生在断面主槽部位。

本节应用一维水沙动力学模型，将6.6.2节中龙门站的计算结果作为输入条件，模拟计算1977年龙门至三门峡河段的水沙过程，然后用1977年龙门站和小浪底站的实测水沙过程模拟计算龙门至利津河段的洪水演进。

6.6.3.3　计算边界条件

悬沙和床沙的粒径分组一致，分组粒径为0.005mm、0.01mm、0.025mm、0.05mm、0.1mm、0.25mm、0.5mm 和1mm。取当前分组粒径及其前一个分组粒径的几何平均为该粒径组的中值粒径。由于泥沙颗粒的最小粒径为0.002mm，所以第一个分组粒径的中值粒径为0.005mm 与0.002mm 的几何平均值。

上、下段存在的支流入汇(上段的汾河、渭河以及下段的伊洛河、沁河，相应的水文站为河津、华县和黑石关、小董)，取同期的实测水、沙过程，存在引水、引沙的下段也相应考虑了同期的引用量。

此外，因缺少1977年三门峡站的水库库容曲线，以及水库泄流曲线，上段的下游端条件，按照三门峡站的历年水位、流量关系给出，不进行水库计算。

根据选用的龙门站水沙过程的不同，模拟分为计算水沙过程与实测水沙过程两部分。

1.计算水沙过程

上段龙门站的入流条件按照6.6.2节中计算的结果 (图6-58、图6-59)给出，演进至三门峡。由于上游的产流、产沙计算暂未给出入流的悬沙级配，入流泥沙过程的级配按照实测沙量过程中的同期悬沙级配给定。

由于上段的模拟都只有进口站的水沙过程，初始条件需要的初始时刻沿程各站的流量、含沙量、水位情况均无法获取，这里简化为沿程各个站的流量、含沙量与进口站一致，而水位则根据沿程流量用恒定流计算得出。初始各站的悬沙级配及床沙级配按照实测沙量过程中的同期悬沙、床沙级配给定。初始条件的不准确，将给计算结果带来较大误差。

模拟时间范围为1977年7月1日～8月31日。

2.实测水沙过程

在该部分的模拟中，上、下段的入口条件均取实测水沙过程，即分别用龙门站和小浪底站的水沙过程为入流条件演进至三门峡站和利津站，入流的悬沙级配也取相应值。初始时刻沿程各站的流量、含沙量及悬沙、床沙级配，均取实测值。水位根据沿程流量用恒定流计算得出。

为了正确对比冲淤量，模拟时间范围为1977年6月1日～10月31日，但在绘制计算与实测水沙过程则选择汛期突出比较。

6.6.3.4　模拟结果

1.上段

上段属于黄河中游的下段，河道宽浅，滩槽不明显，在渭河汇入处干流河道突然收缩进入三门峡峡谷河道，潼关断面河谷宽仅850m，形成天然卡口。潼关以下至三门峡段属于山区峡谷型河道，断面较为规则，长约113km，河谷宽1～6km，河槽宽度500m 左右，平均比降约为0.35‰，潼关河段位于水库回水的末端。

上段长约244km，计算初始地形选用龙门—三门峡的60个汛前实测资料。断面为典型的复式断面，断面宽约为3910m，主槽宽约为1850m。初始各个断面的悬沙、床沙组成，按照汛前龙门、潼关、三门峡站的实测悬沙、床沙组成，通过内插和外延求得。

用1977年实测水沙过程资料率定出的各个流量级下的糙率一般在0.01左右，各个河段变化不大。

支流汾河的同期含沙量、流量较小，就不绘制过程图，而支流渭河的同期流量、含沙量过程中的最大含沙量达700kg/m3，流量达3610m3/s，具体过程如图6-63所示。

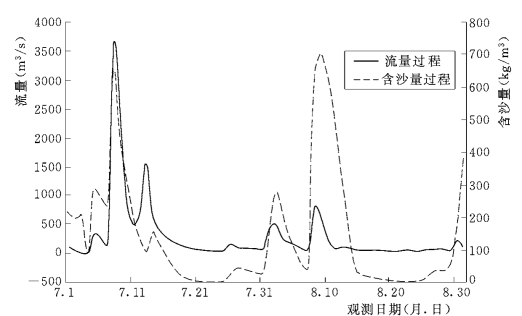
图6-63　1977年7～8月支流渭河的实测水、沙过程 (华县站)

(1)计算水沙过程的模拟。以6.6.2.5节中的龙门站计算结果图6-58、图6-59为入流条件，潼关站和三门峡站的模拟计算结果与实测资料的对比如图6-64～图6-65所示。

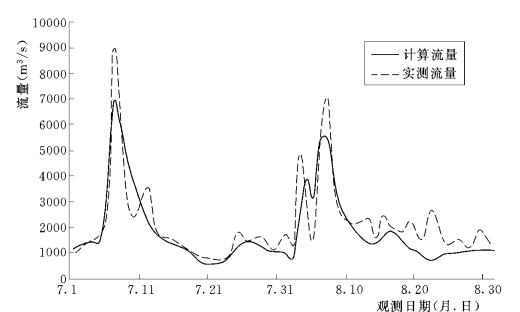
图6-64　1977年7～8月潼关站计算与实测流量的对比图 (计算水沙过程)

通过对计算与实测流量过程的对比可以发现，两个控制站的流量过程的峰值偏小，但是峰现时间基本一致。从表6-7可以看出，流量的峰值差别均较小，且呈逐渐递减的规律;沙量的峰值差别较大，与实测值的误差也逐渐扩大。经分析认为，输沙计算与入口条件及初始条件关系较大，而此次计算的初始条件简化取为各站的含沙量一致，不符合实测各站的悬沙分布规律。

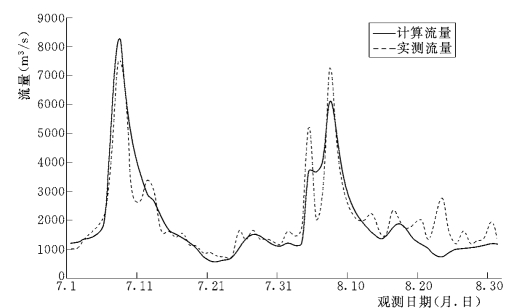
图6-65　1977年7～8月三门峡站计算与实测流量的对比图 (计算水沙过程)

表6-7　1977年7～8月龙门至三门峡河段计算与实测的流量、输沙率峰值对比表

(2)实测水沙过程的模拟。以实测龙门站的水沙过程为入流条件，其水沙过程如图6-66所示。

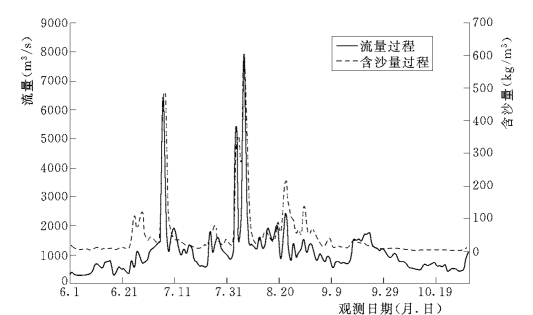
图6-66　1977年6～10月龙门站实测水沙过程图

对该河段进行演进计算，并截取潼关、三门峡两控制站的洪峰段模拟结果与实测水沙过程的对比，如图6-67～图6-69所示。

可以看出，潼关站和三门峡站的计算与实测水沙过程基本一致，模拟结果较好。

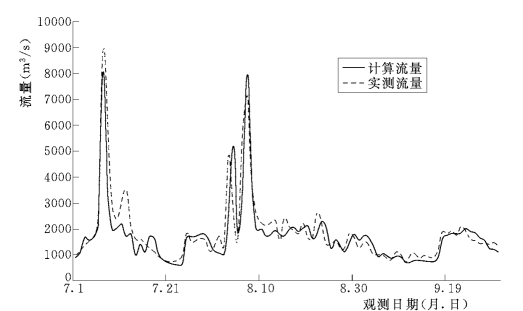
图6-67　1977年汛期潼关站计算与实测流量的对比图 (实测水沙过程)

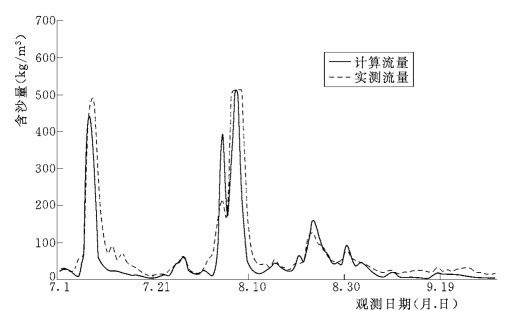
图6-68　1977年汛期潼关站计算与实测含沙量的对比图 (实测水沙过程)

2.下段

下段中的河南铁谢-山东东明高村河段属于游荡性河道，河床宽浅，存在 “二级悬河”，冲淤变化迅速。河道长约299km，堤距宽5～20km，河槽宽1～3.5km，河道比降0.0172%～0.0265%，滩槽高差在2m 以下，平均弯曲系数约为1.15。高村以下则是过渡段及弯曲段。

下段长约740km。计算初始地形选用铁谢—利津的88个汛前实测资料。断面为典型的复式断面，断面宽约为5188m，主槽宽约为1840m。模拟时间范围内最大洪峰流量为7050m3/s。初始各个断面的悬沙、床沙组成，按照汛前花园口、夹河滩、高村、孙口、艾山、洛口、利津7站的实测悬沙、床沙组成，通过内插和外延求得。

伊洛河、沁河两大支流的水、沙量不大，最大流量为477m3/s，最大含沙量仅为64kg/m3。这里就不绘制过程图了。

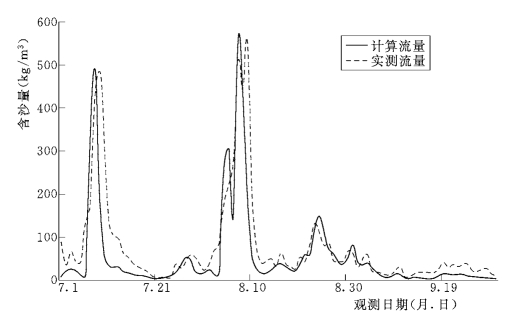
图6-69　1977年汛期三门峡站计算与实测含沙量的对比图 (实测水沙过程)

将小浪底站的实测水沙过程(如图6-70所示)作为进口条件，应用于下段，计算下段河道的洪水演进。

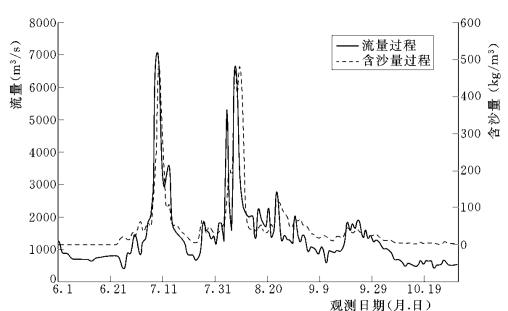
图6-70　1977年6～10月小浪底站实测流量、含沙量过程图

考虑1977年黄河下游各个控制站之间都有引水引沙，这里也增加考虑了引水引沙。简化处理引水闸门的引水方向为垂直于当地河流的主流方向。1977年7～8月的月均引水引沙数据如表6-8所示。

表6-8　1977年铁谢—利津河段的引水引沙

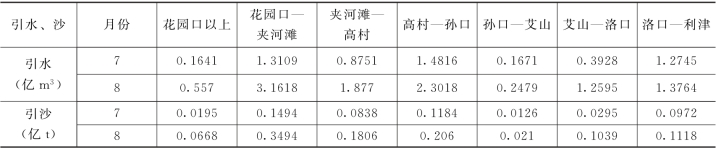
下段的控制站包括小浪底、花园口、夹河滩、高村、孙口、艾山、洛口、利津8站。选取了具有代表性的两站，即高村和利津，分别位于河型转换的过渡段和出口部位，两站洪峰段的计算水沙过程与实测的对比如图6-71～图6-74所示。

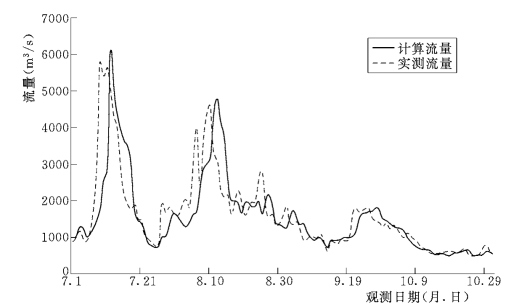
图6-71　1977年汛期高村站计算与实测流量的对比图

图6-72　1977年汛期高村站计算与实测含沙量的对比图

由图可以看出，水沙过程拟和较好。

图6-75给出了小浪底至利津河段的计算冲淤量，与用输沙量法计算的冲淤趋势基本一致。河床演变分析表明，下游是典型的冲积型河道，床沙组成较细，基本为上淤下冲，模拟结果能较好体现这一特点。

从流量过程看，模拟计算出的流量过程与实测的基本一致 (峰现时间)，洪峰峰值差别不大，其差别与模型中糙率的取值方法有关，还与支流控制站的选取有关，如渭河取华县站的水沙过程为汇入黄河主干的水沙过程，而忽略了华县到入汇口段的冲淤变化及演进时间。从沙量过程看，含沙量过程的峰现时间略微滞后，峰值差别不大，拟合程度较好，与上述两个因素有关，也与冲淤分配方式等有关。

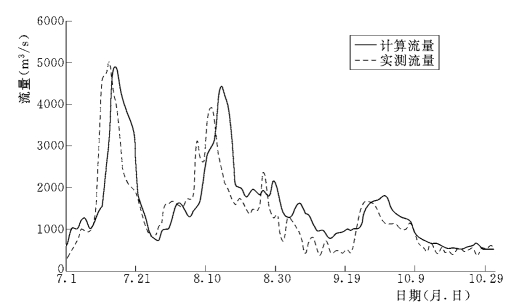
图6-73　1977年汛期利津站计算与实测流量的对比图

图6-74　1977年汛期利津站计算与实测含沙量的对比图

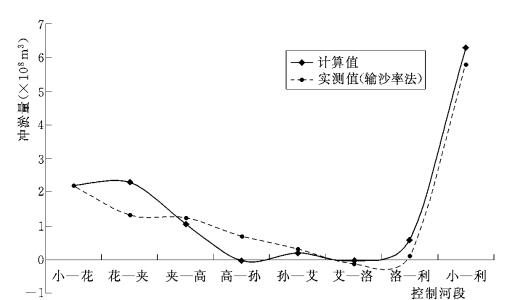
图6-75　1977年汛期小浪底—利津河段计算冲淤量与实测值的对比图

(本章作者:王光谦、李铁键，受国家自然科学基金委创新研究群体基金(50221903资助)