图6-21黄土沟坡重力侵蚀物理图形在垂直坡面方向将沟坡土体分为表层土和中层土。土体重力在降雨期间随土壤含水量发生变化，其两个分量分别是构成下滑力和抗滑力的主要力学因素。该力对土体稳定造成不利影响。沟坡重力侵蚀是在上述各力的作用下，达到临界平衡条件导致的失稳破坏。要正确模拟沟坡重力侵蚀，必须同时对这两类因素加以考虑。沟坡重力侵蚀模型流程如图6-22所示。......
2023-06-22
探析沟坡失稳的不确定性因素
【摘要】：图6-25沟坡失稳问题的模糊性6.5.3.2沟坡失稳的模糊性分析分析沟坡失稳的模糊性，就是要确定该问题中的模糊事件、模糊集以及隶属度函数3个要素。
上述沟坡稳定问题的力学分析中一个隐含的假设是:各力学因素及其相互作用是确定的，或者其不确定性足够小，可以忽略。事实上这是不符合实际情况的，因为沟坡稳定问题不仅包括大量随机因素，而且即使是计算出的安全系数本身也具有一定的不确定性，因此，进行不确定性分析就成为沟坡失稳能否正确模拟的关键问题之一。
6.5.3.1 不确定性的含义
不确定性是自然界各种事物中广泛存在的一种属性。按照其产生条件及表现形式不同，不确定性包括4种类型 (王清印等，2001):随机性、模糊性、灰色性、未确知性。其中灰色性是指由于噪声的干扰和接收系统能力的限制，使得人们只能获取系统的部分信息量的性质。付炜等将灰色系统理论引入重力侵蚀研究并得到一些定量结果。未确知性与主观认识的系统误差有关，该性质与重力侵蚀研究相关性不大且不易量化。随机性和模糊性则反映了重力侵蚀研究中不确定性的两个主要方面，本模型中主要考虑这两类不确定性问题。
(1)随机性。随机性是指由于客观条件的不充分或者偶然外因的干扰，导致对已经明确的结果集合(可能是离散集合或者连续集合)，在某次实际试验中无法预测其在结果集中的位置或值。在沟坡失稳问题中，从严格的意义上讲，由于量测误差、微观物理化学等作用影响，力学因素中的粘聚力、摩擦角等即使对于同一土体，也不是完全确定的值，而是在一定范围内变化的随机变量，由这些量推导出的组合物理量因此也就表现出一定的随机分布特征。
(2)模糊性。模糊性是相对于精确性而言的，是事物类属不分明性以及由此引起的判断上的不确定性，其特点是:对于该事物是否具有某种性态，是否属于某个类别无法用“非此即彼”的唯一确定性来回答，它从属于某一类到不属于该类是逐步过渡而非突然改变的。利用安全系数对失稳与否进行判别就明显具有这种性质，如图6-25所示。
从图6-25中可以看出，安全系数作为安全性的一种特征来评价沟坡失稳状况时，存在一个模糊区间，在此区间外问题具有确定性，例如可认为安全系数小于0.7时失稳一定发生。当数值落入此区间时，安全系数只具有间接反映失稳可能性大小的作用，而不能直接由其数值对失稳事件进行明确判断。所以，这也是需要对沟坡稳定问题进行模糊分析的原因。
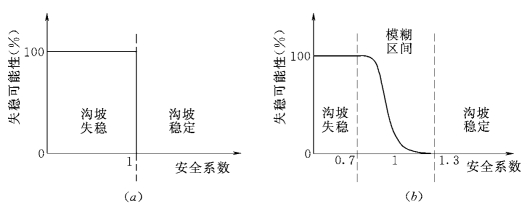
图6-25 沟坡失稳问题的模糊性
6.5.3.2 沟坡失稳的模糊性分析
分析沟坡失稳的模糊性，就是要确定该问题中的模糊事件、模糊集以及隶属度函数3个要素。
1.模糊事件的定义
本问题中，将模糊事件定义为:“该安全系数Fs表示沟坡失稳”，并记为S。因此沟坡失稳问题转化为确定模糊事件S 的不确定性问题，即可利用模糊数学中的理论方法进行分析计算。
2.模糊集和隶属度的定义
设安全系数Fs在某个区间 [0，+∞]内连续变化，则该区间构成问题的一个论域F。于是定义:
式中:A 为从论域F 到区间[0，1]上的映射，构成模糊集，其意义表示Fs在论域中变化时，沟坡失稳的可能性;A(Fs)为定义在论域F 上的隶属度;当Fs为连续型变量时，A(Fs)为隶属度函数。
理论上，问题的论域为 [0，+∞]。但在本问题中，一般情况下由力学分析得到的Fs可能在区间[0，f]上变化，其中f≤2，因此为了计算方便，将该区间定义为问题的实际论域。
3.隶属度函数的确定
上述定义中，沟坡失稳的隶属度函数A(Fs)是将论域中的模糊事件量化为失稳可能性的桥梁，是对模糊集性质的刻画，因此也是沟坡稳定性模糊分析的关键所在。
本问题中，设Fs变化于区间 [0，f]，同时有f1，f2，f3∈ [0，f]且f1＜f2＜f3，则隶属度函数应该满足如下条件:
当 0≤Fs≤f1有A(Fs)=1;(条件1)
当f1≤Fs≤f2及f2≤Fs≤f3时，有0＜A(Fs)＜1;且A(Fs)为分段连续单调减函数;(条件2)
当Fs＞f3有A(Fs)=0。(条件3)
图6-26 不同隶属函数在区间上的分布
在上述条件2中，隶属度函数有多种形式，其选择具有一定的主观性和经验性(胡宝清，2004)。但在模糊分析中为了最大限度客观地反映其中存在的模糊性，模糊分析领域已经将其归结为以下几类:正态分布、Cauchy (柯西)分布、岭型分布、Z型分布等。由于失稳隶属度随着安全系数的增大有减小的趋势，因此可选择上述几类分布中的下降分支。
通过对4种模糊隶属度分布函数在试验区间上([0，1.5])进行数值试验，得到其函数形态如图6-26所示。
对于Z 分布，经过数据对比，需要将原分布中的2 次方替换为4 次方，即如下式所示:
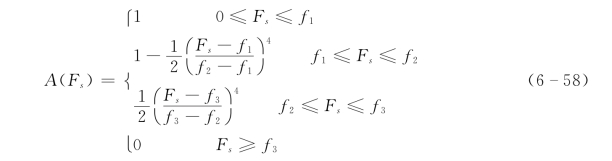
式中:f1、f2、f3分别为Fs在论域上相对于隶属函数值为1，中值和0值的分界点。
由图6-26中可以看出，当安全系数Fs在论域中减小时，Z 分布的失稳隶属函数值趋近于1的速度最快，而当安全系数Fs在论域中增大时，其失稳隶属函数趋近于0的也较大，这种函数形态比较符合实际中当安全系数减小到一定程度，失稳可能性急剧增加，当安全系数增大到一定程度，失稳可能性急剧降低的经验。因此，在上述安全系数变化区间内，Z 分布更接近实际经验，可采用这种分布作为模糊隶属函数。
6.5.3.3 沟坡失稳的随机性分析
沟坡失稳的随机性表现在:其各种影响因素都具有随机性，这些随机因素又相互消涨，使沟坡稳定性总体上也呈现出随机性。罗文强等(1998)将一次二阶矩方法应用于斜坡稳定性概率评价中，并讨论了安全系数与破坏概率的关系;徐卫亚等(1995)利用蒙特卡罗方法对破坏概率进行了分析，并对水布垭坝址基岩的稳定性进行了计算;罗文强等(2000)对矩估计、蒙特卡罗法、函数连分式等几种斜坡可靠度模型进行了对比分析，指出这些方法在精度和难易程度上各有特点。
随机性是用随机变量的概率分布密度来刻画的。沟坡安全系数作为随机变量，其分布特性是由其组成因素的分布特性决定的。
下面讨论安全系数概率密度的确定。
陈立宏和陈祖煜等(2004)利用大量资料，证明了土 (岩)体的粘聚力c和摩擦角φ均可接受正态分布或对数正态分布，同时指出由于正态分布隐含了粘聚力c可能出现负值的情况，与参数本身的物理含义不符;而且粘聚力c本身受含水量影响较大，导致其变异性较大，采取对数正态分布更为适合。此外刘春等 (2003)利用多种概型拟合检验方法，得到了一致的结果。
由式(6-55)及式 (6-56)可知，沟坡稳定安全系数实际上是上述因子的线性组合。因此，可以认为安全系数Fs也是服从对数正态分布的随机变量，其概率密度函数可表示为
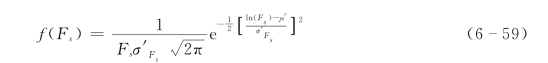
式中:μ′为ln Fs的均值，即为由力学模型计算所得安全系数Fs的自然对数;σ′Fs为ln Fs的标准差，可根据经验或者有关资料选择;Fs＞0;其余各量同前。
实际上，式(6-59)所示的对数正态分布属于偏态分布，较正态分布更能反映各因素的变异性。同时，由于随机变量Fs还位于分母上，从而使得安全系数趋近较小值时的概率有所增大，而当Fs趋近较大值时的概率有所减小，使计算所得结果偏于安全。
6.5.3.4 沟坡失稳的模糊概率
由前面分析可知，安全系数既具有模糊性又具有随机性。要同时刻画这两种不确定性，可以通过计算该变量的模糊概率来实现。
将模糊集合中的事件在其概率空间上进行积分，可以定义该模糊事件的模糊概率测度为
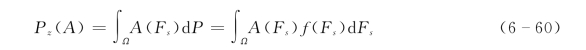
式中:Pz(A)为模糊事件A 的概率;Ω 为概率空间;A(Fs)为安全系数Fs的隶属度函数，由式(6-58)确定;f(Fs)为安全系数的概率密度函数。
6.5.3.5 模糊概率的性态分析
当模糊变量Fs在论域[0，f]上变化时，在隶属度函数与概率密度分布函数的共同作用下，模糊事件“该安全系数Fs表示沟坡失稳”不确定性的变化规律如何，对于沟坡重力侵蚀最终的模拟效果有一定影响，因此，从不同方面分析其变化性态是必要的。
通过假定多组分布参数，可以研究其分布性态的变化特征。下面以一组参数为例，说明其规律。
基本参数:式(6-58)中的f1、f2、f3分别取0.8，1.1，1.5;方差为0.1;计算不同安全系数下的模糊概率分布。
当力学方法计算得到沟坡某时刻的安全系数Fs后，以其对数为均值的模糊概率密度分布，反映了该安全系数在随机因素和模糊因素影响下预示出的失稳趋势，计算结果如图6-27～图6-29所示。
对于不同安全系数的失稳概率分布，模拟计算了两种情况:一是单纯对数正态分布的概率分布情况，即为未记入模糊隶属度的影响;二是同时记入了模糊隶属度以及对数正态分布的情况。
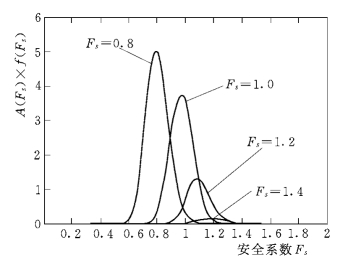
图6-27 记入隶属度影响时不同Fs的概率分布
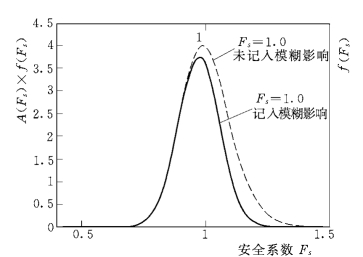
图6-28 Fs=1.0时的失稳概率分布
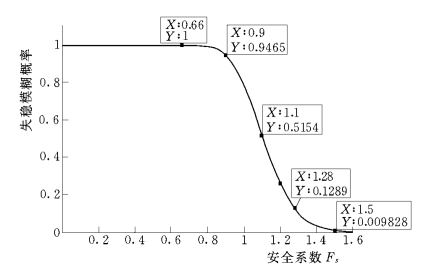
图6-29 各安全系数的失稳模糊概率
从图6-28中可以看到，当未记入模糊隶属度影响时 (如图中虚线所示)，随着均值Fs的增大，峰值有所降低，且峰值所在位置的横坐标为相应的均值Fs，同时曲线由 “窄高”变为 “矮胖”型。而记入隶属度影响的概率分布曲线 (如图中实线所示)，在区间 [f2，f3]上峰值衰减很快，说明随着安全系数的增大，其失稳的概率连续减小的速率也较快。对于同一均值的情况，记入隶属度影响的曲线在安全系数较大的情形下与未记入隶属度影响的曲线相比，其峰值明显偏向安全系数较小的方向，这反映出由于考虑了模糊因素，即使用力学模型计算出了较大的安全系数，但随机可能出现的数值较小的安全系数对失稳的影响仍然被充分考虑进去了。
有关泥沙研究进展的文章
- 详细阅读
- 详细阅读
-
淀粉回生及其影响因素探析详细阅读
淀粉回生是相邻淀粉分子之间羟基基团形成氢键，而发生重结晶的过程。淀粉回生在早期阶段是由直链淀粉引起的，淀粉回生与直链淀粉含量、脂质结合程度和直链淀粉的分子量有关。支链淀粉重结晶是引起淀粉回生的主要因素，且与支链淀粉链长分布关系密切。稻米淀粉的糊化和回生，除与温度密切相关外，水分含量也有显著影响。玉米淀粉中直链淀粉长度接近此值，所以最易回生。......
2023-06-20
-
回应性不足的因素结构的原因探析详细阅读
基于司法国情的现实制约，审判独立在我国尚未实现，多层级主体行使审判权的现状，导致审委会、院庭长都可作为审判权行使主体，对案件处理提出意见。此外，审委会、院庭长对案件审理的指导职能，一定程度上也导致了部分法官产生惰性，依赖于审委会、院庭长对裁判结果的结论，自身不对案件裁判做更深入、透彻的思考，在此情况下法官也难以进行充分说理。囿于激励机制的缺失，是说理招致诟病的另一因素。......
2023-07-18
-
胶接机理及其影响因素探析详细阅读
胶接过程是一个复杂的物理、化学过程。胶接力的大小，不仅取决于胶粘剂和被粘物表面的结构和状态，而且和胶接过程的工艺条件等密切相关。吸附理论把胶接主要归结于胶粘剂与被粘物分子间力的作用。吸附力是提供胶接力的普遍因素，但不是唯一因素。......
2023-06-26
- 详细阅读
-
矿山安全工程学：影响边坡稳定性的因素分析详细阅读
了解和掌握引起边坡破坏的因素和影响程度，对确定边坡的稳定性和预防管理方法非常重要。表示弱面呈水平，此时的边坡比较稳定。因此抵消了作用于滑动面的正应力，最终导致滑动面上的摩擦阻力减小，这是不利于边坡稳定的。动水压力是推动边坡向下滑动的，一般能使下滑力增加24%，因此它对边坡的稳定性是极为不利的。......
2024-07-05
-
公路设计与施工：纵坡和坡长的重要规定详细阅读
表2-10 《标准》中规定的各种设计车速下的最大纵坡坡度表2-11 《标准》中规定的各种设计车速下的公路纵坡长度限制2.6.4.2 国内外对纵坡和交通事故等方面的研究日本规定纵断面线形应连续，避免生硬而剧烈变化的线形。很明显在积沙路段，纵坡6%的阻力比纵坡5.5%的大1.41倍；纵坡7%的阻力比纵坡5.5%的大1.84倍。......
2023-09-22
相关推荐