验证沟道水沙计算的有效性

2023-06-22 理论教育版权反馈

【摘要】：采用高含沙引水渠道的实测资料验证上述沟道水沙计算模型。恢复饱和系数取为0.1。图6-20部分实测资料的τB～Sv关系从更深的层次讲，沟渠中的高含沙水流与干流河道的水流不同，容易出现非牛顿体伪均质流的现象。可以看出，在这一判别准则下，沟道高含沙水流很容易进入到非牛顿体状态，从而使沟道水沙模型需要包含非牛顿体模型以反映真实的物理图景，这将成为进一步的研究方向。

采用高含沙引水渠道的实测资料验证上述沟道水沙计算模型。洛惠渠位于陕西关中东部，水源为北洛河。北洛河发源于陕北定边县白宇山区，为黄河多沙支流之一，多年平均流量25.7m3/s，年输沙量9.5×107t，汛期最大含沙量接近1100kg/m3(状头站)。总干渠由状头引出至义井分为东、中、西三条干渠。其中东干渠比降1∶3000，渠道为梯形断面，底宽2.2m，边坡1∶1.5。设有东干渠义井测验断面，距渠首884m (人民引洛渠高含沙量浑水淤灌组，1978)。

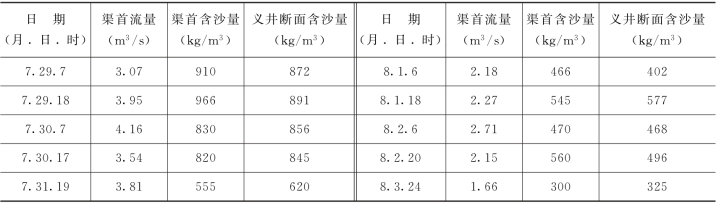
采用1974年7月29日～8月3日东干渠渠首与义井断面实测水沙过程，实测资料如表6-1所示。

表6-1　1974年洛惠东渠实测资料

pagenumber_ebook=314,pagenumber_book=298

仍将渠道断面简化为Ⅴ形，并根据当时断面实测情况取m=2，糙率n 取为0.04，中值粒径为0.035mm，上限粒径取为0.080mm。时间步长取为12min，空间步数为2，入口水沙过程线性内插。恢复饱和系数取为0.1。计算结果如图6-18 所示。可以看出，张红武公式和费祥俊公式都能较好符合实测资料，并与渠段淤积的情况相一致。

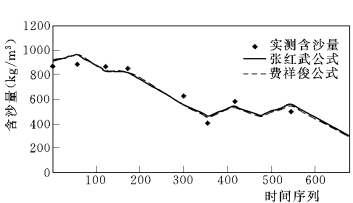
pagenumber_ebook=315,pagenumber_book=299

图6-18　出口断面的含沙量过程验证

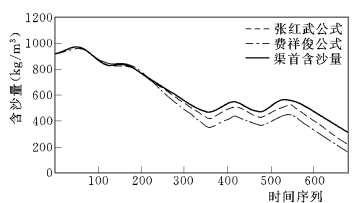
pagenumber_ebook=315,pagenumber_book=299

图6-19　恢复饱和系数置为1时的出口含沙量过程

为较为直观地分析影响两个挟沙力公式计算数值的主要因素，将恢复饱和系数取为1，此情况下的计算结果如图6-19所示。费祥俊公式的含沙量计算结果略小于张红武公式，这可能与其公式率定的水力半径值较小 (R=0.05～0.10m)有关。然而，从挟沙力公式的形式上看，费祥俊公式沉速的幂次较高，通过ω90的形式更多地反映了来沙情况的影响，更能符合黄土高原产沙区沟道多来多排的输沙特征。

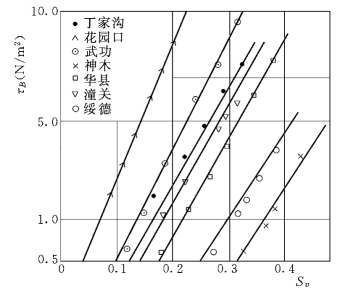
pagenumber_ebook=315,pagenumber_book=299

图6-20　部分实测资料的τB～Sv关系 (费祥俊，1991)

从更深的层次讲，沟渠中的高含沙水流与干流河道的水流不同，容易出现非牛顿体伪均质流的现象。对于非牛顿体的水沙运动，费祥俊(1991)以τB=0.5N/m2作为牛顿体过渡到非牛顿体的判别准则，并得到部分实测的非牛顿体含沙量如图6-20所示。可以看出，在这一判别准则下，沟道高含沙水流很容易进入到非牛顿体状态，从而使沟道水沙模型需要包含非牛顿体模型以反映真实的物理图景，这将成为进一步的研究方向。

验证沟道水沙计算的有效性

相关推荐