但需要注意的是，连续方程式和运动方程式是相互耦合的。连续方程和运动方程的离散方程中，当采用线性化方法处理时，系数可由当前时刻的流场计算得到。第②、③步组成PISO循环，直至校正流速与预测流速之间的误差小于给定阈值。在PISO循环结束后，调用紊流模型和水质模型进行模拟，然后转入下一时间步的计算。......
2023-06-26
精确扩散波汇流模型的优化方法
【摘要】：这一条件为以上即为贡日提出的马斯京根形式的扩散波方法。
6.4.1.1 马斯京根—贡日法
圣维南方程是描述明渠一维非恒定流动的基本方程，水深h 形式的方程如下:
式中:t为时间;x 为沿河坐标;u 为流速;B 为水面宽度;S0为河底坡降;Sf为摩阻坡降。
贡日(Cunge)讨论了马斯京根法与水动力学法的关系 (杨国录，1993)，在扩散波方程和马斯京根法之间建立了联系。令扩散波方程D=0，则为更简单描述水流运动的运动波方程。贡日指出，运动波方程的空间偏心四点离散求解方法具有马斯京根法的形式，即:
其中
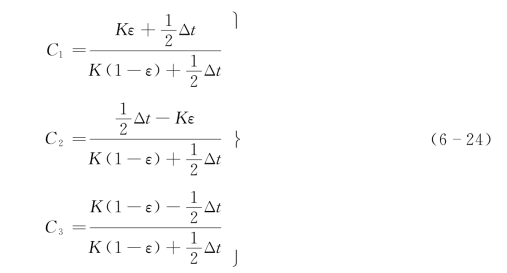
通过数学推导证明，式(6-23)的数值格式在一定的条件下是二阶逼近式 (6-22)的。这一条件为
以上即为贡日提出的马斯京根形式的扩散波方法。其稳定条件为
通过式(6-25)可以看出，在Q，B，C，Δx，Sf＞0的正常情况下，算法的稳定性是无条件的。同时，对算法收敛性的研究表明，柯朗数r=CΔt/Δx 越接近1，其收敛性越好。
6.4.1.2 时空步长的选择
模型的时间步长是在运算前约定的，为小时的整数分之一，如10min、6min、3min、1min等。为获得更高的模拟精度，需要选择较小的时间步长;而在一定的问题规模和计算能力下，为使计算耗时能够承受，又不能使时间步长过小。
模型应用时，河网中每个河段的长度不同，所经历的洪峰流量等水力要素也不同，甚至存在着巨大的差异。为在这样的情况下使数值格式的收敛条件能够得到满足，并减少负反应的出现，需要逐河段确定合理的空间步长。
负反应多是伴随C2、C3的负值出现的，为控制负反应，要求式 (6-24)中C2、C3均不小于0，将式(6-25)代入，可解得
另一方面，收敛性要求
以上两式的条件是不冲突的，因此，在计算中取Δx=CΔt，其中C 值以洪峰条件下的波速计算，以使洪峰的模拟具有更高的精度。则特定河段的分段数N 由下式确定:
式中:L 为河段的长度;Int( )为取整运算。
6.4.1.3 水力要素的计算
挟沙能力的计算需要计算点的水力要素值。数值格式中多是取计算网格部分点的均值。在显式格式中，多取已知3点，即(j，n)，(j，n+1)，(j+1，n)的平均值;而包含(j+1，n+1)点在内的4点平均则形成了需要迭代计算的隐格式。Tang X.等 (1999)通过数值实验证明:4点平均的格式在计算结果对时空步长变化的稳定性和水量守衡等方面存在一定的优势。因而，采用如下计算方案:
水力要素计算的核心是波速C 的计算。为由Q 计算C，首先引入断面形状假定。费祥俊(2004)认为，小流域沟道过流断面一般可概化为“Ⅴ”形，如图6-16所示。
在“Ⅴ”形断面下，波速与流速的关系为
式中:U 为流速。
在上述断面假定下
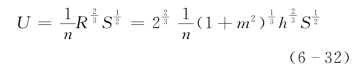
图6-16 沟道过流断面形状假定
式中:n为曼宁糙率;S 为谢才公式的水力坡降。
Cappelaere B. (1997)曾经指出，在扩散波方程系数的求解中，如果假定水力坡降等同于河床坡降，则恰恰忽视了扩散波方法与运动波方法中的本质不同，即对式(6-21)中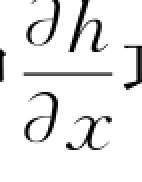
项 的考虑。本方法取
式中:η为系数，其取值范围为
综上所述，通过断面形状假定和谢才公式的应用，得到了直接由流量条件推求扩散波方程系数的方法，从而使扩散波方程能够应用于沟道。
6.4.1.4 验证与对比
将上节中的方法应用于Ⅴ形断面顺直河道，并与水动力学方法和马斯京根法对比。
假定河道参数如下:L=100km，S0=0.00025，m=4，n=0.035。
计算中取Δt=1h，N=15，涨水时η=0.75。计算演进结果如图6-17所示。
需要指出，上述方法的精度并不是扩散波方法所能达到的上限。Cappelaere B.的精确扩散波方法从理论上证明了其精确度，但在应用时仍需要通过统计资料率定重要参数。为舍去参数率定的过程而采用了谢才公式计算扩散波方程系数，从而损失了模拟的精确度。但对于无断面资料与实测资料的沟道而言，这一方法已在有限的已知参数的情况下，尽大可能的提高了水流演进的精度，不失为一种沟道水流演进的精确扩散波方法。
有关泥沙研究进展的文章
- 详细阅读
-
模型验证计算的优化方法详细阅读
模型用于待建工程计算前，应进行天然河道率定。最大输沙率计算值为0.16615kg/s，发生在7920s，沙峰试验值较计算值滞后。最大输沙率试验值与计算值之比1.69。验证计算结果见图9-25。......
2023-06-22
-
CDAR模型优化方法详细阅读
1985年，Seaman 和Curran 采用统计平均的方法，建立了模拟准脆性材料动态拉伸断裂与破碎的微裂纹细观损伤模型，得到了岩石材料在加载过程中的裂纹尺寸及分布的演化［14］。在此基础上，Matheson［20～23］提出了损伤与化学反应耦合模型 。CDAR 模型包括一个黏弹塑性模块和一个拉伸损伤膨胀模块，可以描述含能材料内部脱黏颗粒附近孔洞变化以及黏结剂开裂产生的微裂纹的张开和闭合。塑性体积膨胀应变率表示为......
2023-06-27
-
建立被控对象模型的优化方法详细阅读
炮控系统是一个较为复杂的系统，在研究过程中，可以先以炮塔电动机和其功放部件晶体驱动器为被控对象，进行研究。用示波器观测测速电动机的输出得到控制结果，检验自抗扰控制器的控制性能。图5.4系统原理2.高低向稳定器建模以图5.5所示高低向电液炮控伺服系统为对象讨论并建立其数学模型[106-110]，它由陀螺仪、放大器、液压系统、火炮等部件组成。......
2023-06-24
-
扩散连接设备的组成优化为：扩散连接设备的主要详细阅读
不论何种加热类型的扩散连接设备，均由以下全部或其中的几部分组成。电阻加热真空扩散连接设备采用辐射加热的方法进行连接，加热体可选用钨、钼或石墨材料。扩散连接设备一般采用液压或机械加压系统，在自动控制压力的扩散连接设备上，一般装有压力传感器，以此实现对压力的测量和控制。......
2023-06-26
-
材料本构模型的优化方法详细阅读
炸药颗粒采用各向同性的弹塑性本构模型。式是根据松弛条件本构方程，通过将一点的应变分解为应变球张量和应变斜张量两部分推导得到的。用Prony 级数表示黏弹性属性的基本形式为式中：和Gi为剪切模量；和Ki为体积模量；和为各Prony 级数分量的松弛时间。表7－7剪切松弛模量与松弛时间的关系......
2023-06-27
- 详细阅读
-
建立操作机构仿真模型的优化方法详细阅读
通过ADAMS软件提供的图形接口模块，将三维实体造型软件UG中建立的机构三维模型导入到ADAMS软件中的。考虑到所关心的问题和仿真的方便，对操作机构作适当简化后，用ADAMS软件包建模。约束关系的添加要充分考虑实际操作机构中可能存在的约束，遗漏任何一个约束关系都会严重影响到输出结果。3）仿真过程的控制 在ADAMS软件中，为了实现对仿真过程的控制，需要添加传感器来控制仿真过程的自动终止。......
2023-06-15
相关推荐