悬沙和床沙粒径悬殊范围更大。现在有关数学模型分组挟沙力计算方法和下面的讨论都是相当近似的。......
2023-06-22
挟沙能力公式的应用技巧探究
【摘要】：作者在前面关于挟沙能力公式结构形式分析时，曾经直接拟合张瑞瑾等原始公式，得到张瑞瑾公式的指数应该为式 。
5.6.1.1 挟沙能力公式指数的合理范围
张瑞瑾公式，挟沙能力和泥沙沉降速度成反比，表明泥沙越细、挟沙能力越大这是完全合理的。但是，根据不平衡输沙的河床冲淤方程，单组泥沙冲淤强度具有如下形式:
在上游来沙较少的冲刷情况下，有理由得到
根据这一公式，如果假设不同分组泥沙恢复饱和系数为常数，比如都取1，而且取挟沙能力公式的指数m＜1.0，式(5-112)表明明显冲刷情况下，粗泥沙冲刷强度远大于细泥沙。一般，在实际计算中，较粗沙分组泥沙的沉速比细泥沙分组大几个数量级，可见上述强度差别是非常严重的。换言之，冲刷后床沙将趋于细化。在水流强度比较低、没有进入普遍冲刷状态的范围内，这是明显不合理的。
作者在前面关于挟沙能力公式结构形式分析时，曾经直接拟合张瑞瑾等(1993)原始公式，得到张瑞瑾公式的指数应该为式 (5-37)。在通常情况下(U 3/g Hω ＜1000)指数都是大于1的。而U 3/g Hω ＜1000是长江、黄河主要资料的范围。可见，张瑞瑾等原始公式不会具有上述问题。至于输沙强度极强，所有泥沙都处于高强度冲刷的条件下，是否粗沙更容易冲刷的可能性是存在的，但需要认真研究。但是，目前泥沙数学模型对挟沙能力系数和指数的选取非常混乱。很多泥沙数学模型，包括很多在三峡和黄河重大工程中大量应用的模型都选取小于1的挟沙能力指数，其合理性值得研究。
5.6.1.2 平面二维模型挟沙力计算的问题
张瑞瑾公式是根据重力理论得到结构公式，然后依据断面平均的水沙资料经过回归分析等得到断面挟沙能力。理论上讲，这一公式应该适用于断面任意垂线，但是，由于该公式是非线性的，直接利用这一公式计算断面挟沙能力分布存在严重问题。
对如图5-126所示意的一个河道断面。根据垂线流速直接应用张瑞瑾公式于垂线，可计算出每个垂线的挟沙能力。由断面挟沙能力分布平均得到的断面平均挟沙能力 (图5-126中A)和根据平均流速和水深计算得到的断面平均挟沙能力 (图5-126中B)存在很大差别。通常前者大于后者，二者相差的幅度较大。对于滩槽明显的河道，有时差别可以达到一倍以上。应用这一公式和平面二维模型计算黄河河道冲淤时，常常发现主槽严重冲刷现象。作者发现，其主要原因就在于计算主槽挟沙能力严重偏大。如果假设张瑞瑾公式在一维河道是正确的，则有理由肯定:这一公式不能直接应用于平面二维泥沙数学模型，应用时必须对系数进行修正。关于修正方法，作者在二维数学模型计算中进行了一些初步的尝试和试验，取得一定的改进效果。但是，迄今没有得到普遍适用的公式。如何从理论上系统解决上述问题，仍然值得深入研究。
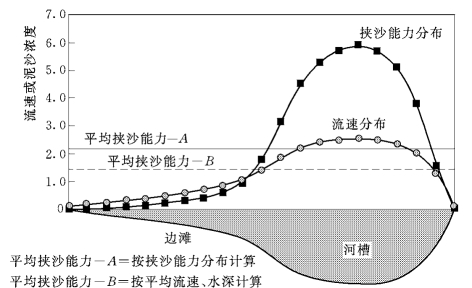
图5-126 根据式(5-36)计算断面挟沙能力分布存在问题示意
或者也有理由反过来认为，对天然河道，断面平均挟沙能力大小应该和断面形状等有关系。张瑞瑾公式的系数和指数不能反映这些特征、过分简化，可能使一维挟沙能力在有些断面情况下也不一定准确，这是公式的缺陷。比如，利用天然河道相对浅水的资料得到的挟沙能力公式(比如长江中下游资料)是否适用于水库泥沙计算 (比如三峡水库)，如果适用，其系数和指数应该如何选取更合理? 这些都是值得深入研究的问题。
有关泥沙研究进展的文章
- 详细阅读
-
大河流输沙能力公式详细阅读
Einstein 认为，水流的输沙能力与水流克服沙粒阻力所要求的能坡J′有关，而不是总能坡J。式表示的关系式与Velikanov、张瑞瑾、窦国仁分别提出的式 (2-2)、式(2-4)、式(2-5)表示输沙能力关系的形式基本相同。因此，在大河流的输沙能力计算公式中，选择合适的阻力公式，将比降表示为速度和水深的函数，是一种较为有效的处理办法。根据表2-1给出的414组大河流输沙资料点绘了Ct与Ψ 的关系，见图2-4。......
2023-06-22
-
水流输沙能力公式的修正方法详细阅读
由此可见，含沙量对水流输沙能力的影响是十分显著的，是造成多沙河流输沙能力不同于少沙河流的重要因素。为了解决生产中所提出的问题，不得不依赖于一些经验性输沙能力公式。......
2023-06-22
-
预测公式的建立方法及应用技巧详细阅读
图3.14抗压强度与水泥土电阻率的关系式中：ρst、ρs7分别为相同浓度下龄期是t d和7d的水泥土电阻率值；t为龄期，天；G、H 为常数。由表3.7中的回归分析可知，特定龄期下水泥土电阻率与浓度的关系可用以下通式表示：式中：ρs为水泥土的电阻率值；C为溶液浓度，g/L；P、Q为常数。式即为含氯化镁污染土的水泥土电阻率预测公式，此关系式的预测值和实测值对比见表3.8和图3.15。图3.15电阻率实测值与预测值对比图......
2023-06-26
-
坡面产沙计算公式详解详细阅读
图6-9坡面侵蚀单元设泥沙颗粒顺坡的平均运动速度为vs，则单位时间内单位宽度坡面上通过观察面流出的泥沙所占面积为vs，即图中阴影部分的面积。将此关系代入式得到在较小尺度的坡面上，由于降雨近似均匀，单宽流量q 与单位面积上的径流量qe存在关系:q=qex，其中x 为沿坡面向下的坐标。由于坡面概化为矩形斜坡，设坡面面积为A，坡长为L，则坡面的宽度B=A/L。......
2023-06-22
-
探究立体投影技巧与应用介绍详细阅读
3-6求半圆球的水平投影及表面上线的投影。3-7分析下列各平面立体的截交线，根据它们的两面投影求第三面投影。3-12画出第三视图，并分析题与题、的对应关系。3-14补画出相贯线的正面投影。3-28补全柱锥相交的水平投影。3-30补全半球被柱面挖切后的正面和侧面投影。......
2023-06-15
-
潮流和波浪对沙的剥蚀能力详细阅读
我国河口海岸多为粉沙和淤泥所覆盖，在风浪和潮流的共同作用下，泥沙极易悬浮和输移。该地区的挟沙能力与风浪和潮流的能量有关。波浪能量的损耗可近似认为与其本身能量成正比。如果用R1和R2分别表示波浪和潮流在单位时间内用以悬浮泥沙所消耗的能量，则根据前述可以写出式中:β2和α0均为系数。......
2023-06-22
-
桥涵水文学：基于输沙平衡原理的公式详细阅读
64-2公式是根据我国桥梁实测洪水冲刷观测资料，参照国外同类公式，依据桥下河槽输沙平衡原理建立的，具有坚实的理论和实践基础，比较符合我国河流桥下一般冲刷的实际情况。根据桥下河槽断面的输沙量平衡条件，可导出一般冲刷计算公式。式与式原理相同，计算结果相差不大，但简明易用，均适用于沙质河槽的一般冲刷，《公路工程水文勘测设计规范》中推荐使用。......
2023-11-20
相关推荐