本节的全三维不恒定流和泥沙数学模型基本方程建立在平面正交曲线坐标和立面σ坐标系下:5.5.1.1水流运动基本方程连续方程平面ξ方向的动量方程连续方程平面ξ方向的动量方程平面η方向的动量方程平面η方向的动量方程垂线σ方向的动量方程垂线σ方向的动量方程动量方程式~式中DP1,DP2,DP3项分别为压力P=pa+ps+pd在ξ,η,σ方向上的梯度项,pa为水面处大气压强,ps为静水压强,pd为动水压强。......
2025-09-29
5.5.6.1 二次流弯道横向冲淤变形的作用
二次环流对悬沙的横向输运的作用 图5-118是根据数学模型计算的典型弯道的二次环流。在二次流的作用下,表面附近水流从凸岸向凹岸运动,在弯道凹岸阻挡下进一步俯冲折向床面,再沿着河底从凹岸流向凸岸沙洲边缘,进一步和弯道的横向流相遇并从河底向自由水面方向运动。这样,二次流将表面含沙量相对较低的水流带到凹岸河床,加速凹岸冲刷。同时,底部的二次流从凹岸指向凸岸,将含沙量相对较高的水流搬运到凸岸,增加凸岸淤积的机会。当二次环流强度较大、悬沙沉速较小时,二次环流的横向混合作用就越明显。这就是弯道河床冲淤演变,形成凸淤、凹冲河型的力学机理。
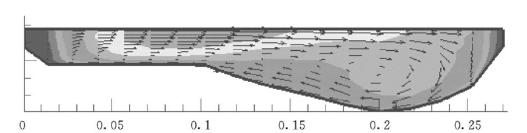
图5-118 根据三维数学模型典型弯道二次流计算结果
图5-119运用本模型计算一个180°弯道的泥沙浓度分布情况。在弯道段,在主流和二次环流作用下的水流含沙浓度平面分布表明,凸岸浓度明显高于凹岸。弯道凸岸泥沙浓度较大,然而由于水流流速小、挟沙力小,泥沙可能处于超饱和状态,因此在凸岸边滩发生淤积;而在弯道的凹岸悬沙浓度小,水流流速较大,紊动较强,水流挟沙力较大,含沙量处于次饱和,因此在凹岸附近区域可能会发生冲刷,在弯顶下部由于主流的冲顶可能使得当地河岸和河床发生较大的冲刷。
二次环流对推移质横向搬运的作用 二次环流对推移质输运作用存在争论,焦点在二次环流对推移质泥沙运动影响程度方面。用三维模型研究了弯道上推移质运动。

图5-119 二次流对悬沙的横向运动的影响 (三维数学模型计算结果)
模型计算da Silva (1995)所做的弯道实验的条件计算推移质运动。实验弯道长1103m,宽20m,弯道断面形态采用梯形概化,床面的边坡为1∶3,河道纵比降为1∶1120,流量为35.2m3/s,出口水深为1.5m。为了便于观察推移质输沙率在弯道上的空间分布,床面没有铺沙,只在进口给定恒定单宽推移质输沙量qb,平衡推移质输沙率采用Van Rijn公式计算。本算例水流计算时间步长0.1s,泥沙计算步长5.0s,泥沙粒径0.36mm。推移质非平衡输沙调整长度Ls=2Δx,Δx 为计算网格长度。
模型计算的底层和表层水流形成的剪刀流分布如图5-120。可以看出,表层水流流速较大并有向弯道凹岸方向运动的趋势,而底层水流流速较小并有向凸岸方向运动的趋势。
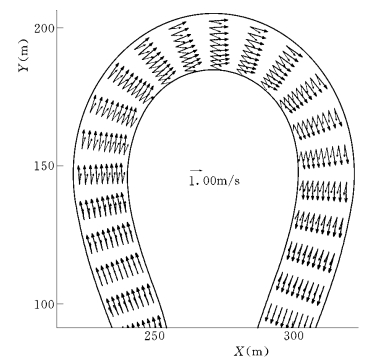
图5-120 弯道底层和表层剪刀流动分布
在考虑和不考虑二次流的情况下,对推移质的运动形态进行了计算。后者是在求解推移质运动时假设水流在横向的流速为0。在考虑和不考虑二次环流输运作用下,推移质输运模型计算的推移质单宽输沙率在某一时刻的空间分布如图5-121所示。在不考虑二次流作用时,推移质从上游以较为均匀的速率运动到下游;而考虑二次流影响时,推移质泥沙就会在底层流速的作用下逐渐向弯道的凸岸运动。从模拟结果可以定性看出弯道二次环流的横向流速分量对推移质的运动有一定程度的影响,如果不考虑弯道二次环流的作用,推移质模型计算中,推移质输运带将不会向弯道凸岸靠近。在许多卵石河床凸岸出现较大的卵石堆积体,也与横向环流有一定关系。
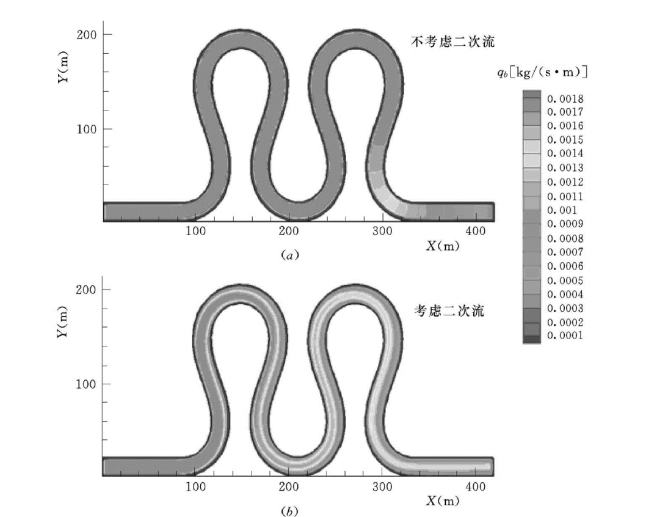
图5-121 数学模型试验:比较二次流对推移质单宽输沙量的影响
5.5.6.2 弯道演化试验及计算对比(https://www.chuimin.cn)
Nagata等(2000)等试验了连续蜿蜒河道的展宽演化过程。利用这一试验来对比和检验具有横向展宽和变形的模型计算结果的合理性。实验的水槽和横断面形状如图5-122所示。水槽长10m,宽1m,深0.2m,弯道的初始形态采用正弦函数生成,波长为2m,初始横断面为梯形,断面的底宽为14cm,顶宽为30cm,河岸高为4cm。实验流量为1.98cm3/s,水深为3.0cm,断面平均流速为33.0cm/s,河道纵比降为1/300。水槽中泥沙比较均匀,平均粒径为1.42mm,![]() 最初的河道比降为弯曲型。试验弯道共包括四个波长,实验数据从第二波长河段获取。实验过程中在水槽上游人工喂沙。泥沙主要以推移质的运动形式存在,计算不考虑悬移质。模型计算设网格260×18×12个,水流计算步长0.01s,泥沙Schmidt数σc取为0.8,泥沙时间步长20s。
最初的河道比降为弯曲型。试验弯道共包括四个波长,实验数据从第二波长河段获取。实验过程中在水槽上游人工喂沙。泥沙主要以推移质的运动形式存在,计算不考虑悬移质。模型计算设网格260×18×12个,水流计算步长0.01s,泥沙Schmidt数σc取为0.8,泥沙时间步长20s。
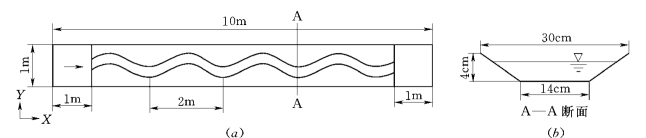
图5-122 Nagata等 (2000)试验水槽平面和弯道横断面示意图
图5-123 (a)是其第一组试验第二个弯段的变化情况。数学模型计算模拟了这一弯道横向变形情况。在这一例子中,由于凸岸流速大,弯道演变的形式主要以凸岸冲刷和展宽为主。而凹岸流速偏小,基本没有发生冲刷。演变过程中河道弯曲程度有所减小。数学模型模拟结果和实验结果吻合良好。
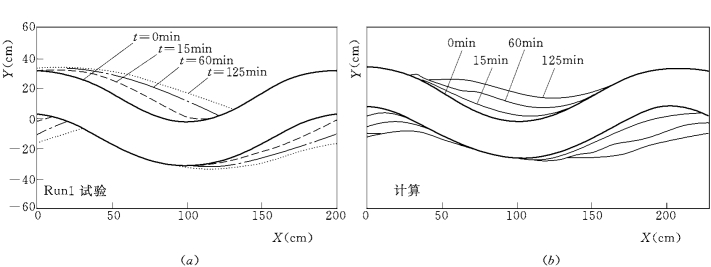
图5-123 实测和模型计算的弯道平面变化对比图
5.5.6.3 河岸固定情况下弯道上浅滩和深槽的形成模拟
河道中浅滩、深槽和对角沙洲的形成和发展是弯道变迁的重要原因,模拟这种河道形态具有重要意义。在固定河岸条件下,应用三维模型来模拟河岸不可冲情况下弯道浅滩和深潭的形成及其发展过程。计算采用Friedkin (1945)试验自由弯道的初始地形,考察河道演变初期浅滩和深槽的形成过程。采用流量0.014m3/s,河道比降为0.007,初始横断面为梯形(表面宽0.6m,底宽0.32m)。模型网格数为220×22×22,取泥沙Schmidt数σc为1.0。泥沙时间步长为20s。模型计算弯道水深变化及其弯道顶部偏下位置横断面(Cs)的形态、主流流速大小分布及二次环流场的分布如图5-124所示。在计算初期,弯道横断面为梯形分布,在整个横断面都有二次环流分布,且二次环流的强度较弱,随着弯道浅滩和深槽的发展,主流流线变得更加弯曲,二次环流的强度越来越大,但二次环流的流动范围只分布在深槽附近区域,在浅滩区域有明显的横向流分布。与此同时,弯道浅滩和深槽有向下游发展的趋势,二次流的冲淤作用在下游直段仍有影响,弯道下游顺直段上也有浅滩和深槽相间的分布。Friedkin (1945)试验完整模拟出自由弯道的发展变化过程,Olsen (2003)也通过数学模型初步计算出上述弯道发展过程。由上述初步结果可见,用本三维可能模拟出自然弯道的发展的基本要素 (浅滩和深槽的形成)。模型模拟Friedkin试验的相关研究正在进行中。
5.5.6.4 蜿蜒河道发展模拟
蜿蜒弯曲河道的发展演化是通过纵横方向冲淤变形产生的移动来实现。模拟计算了da Silva连续弯道的进一步弯曲变形的过程。
在弯道发展过程中凹岸深潭和凸岸沙洲的形成、发展和稳定程度对弯道蜿蜒发展有较大的作用。随着浅滩和深槽的发育,弯道主流流路弯曲程度增加、二次环流的强度变大,在二次环流的横向输运作用下弯道的凸岸浅滩也得到较好的发育(图5-125)。
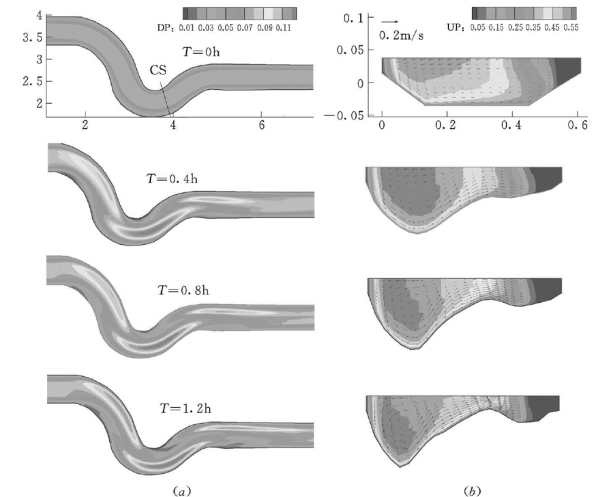
图5-124 固定边岸情况下弯道浅滩和深槽的形成模拟
(a)水深;(b)弯道定点CS从下游向上游看的环流分布
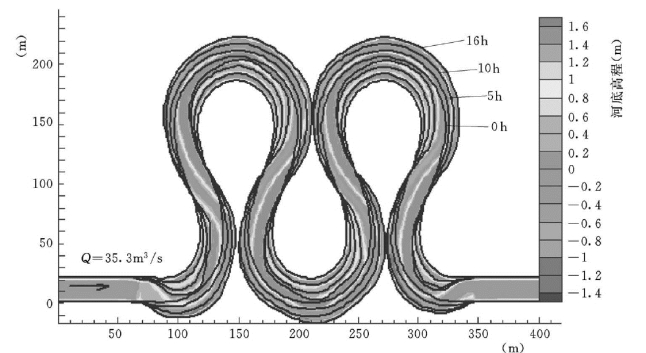
图5-125 成形弯道的发展过程 (模型模拟结果)
相关文章

本节的全三维不恒定流和泥沙数学模型基本方程建立在平面正交曲线坐标和立面σ坐标系下:5.5.1.1水流运动基本方程连续方程平面ξ方向的动量方程连续方程平面ξ方向的动量方程平面η方向的动量方程平面η方向的动量方程垂线σ方向的动量方程垂线σ方向的动量方程动量方程式~式中DP1,DP2,DP3项分别为压力P=pa+ps+pd在ξ,η,σ方向上的梯度项,pa为水面处大气压强,ps为静水压强,pd为动水压强。......
2025-09-29

5.4.3.2杭州湾不恒定流及泥沙计算图5-73用平面二维泥沙数学模型计算三峡坝区泥沙浓度和泥沙淤积情况平面二维泥沙数学模型在计算三峡坝区泥沙浓度收敛过程 ;平面二维数学模型计算三峡坝区泥沙淤积时,比较沿程断面流量守恒情况图5-75杭州湾不恒定流水位、流速和泥沙浓度验证情况5.4.3.3葛洲坝三江上下游引航道的不恒定流验证图5-74杭州湾地理位置和计算区域示意图杭州湾位于钱塘江出海口,如图5-74所示,是一个强潮型河口。......
2025-09-29

图5-112中性物质在弯道中图 ,图 和图 连续排放的平均浓度验证图5-112中性物质在弯道中图 ,图 和图 连续排放的平均浓度验证图5-113试验深槽以及垂向计算网格示意图图5-113试验深槽以及垂向计算网格示意图图5-114计算深槽水流结果与Van Rijn 试验及Alfrink 计算结果比较5.5.5.3深槽水流、 泥沙计算验证图5-114计算深槽水流结果与Van Rijn 试验及Alfrink 计算结果比较5.5.5.3深槽水流、 泥沙计算验证Van Rijn 在进行了多组不同尺寸和流量的水流跨过深槽的水槽实验。......
2025-09-29

在三峡论证期间,确定了三峡工程采用五级船闸结合垂直升船机方案解决三峡枢纽通航。图5-87二维泥沙数学模型计算结果显示,三峡运用后期引航道口门段存在严重的淤积但是,将升船机和船闸同时包括在引航道内又导致船闸充水波动对升船机的影响和引航道内部泥沙淤积和清淤等问题。......
2025-09-29

图5.37混凝土面层爆破及裂纹扩展模型假设爆燃反应气体产物等熵膨胀,裂纹内气体体积可表述为式中,a为裂纹长度;W为活性聚能侵彻体爆燃反应深度。图5.39环向裂纹及抛掷效应分析模型以有效活性聚能侵彻体等效起爆中心为原点,爆燃反应冲击波呈球形在跑道各层介质中传播,产生径向压力波,强度随传播距离衰减。图5.40混凝土面层底部压力分布模型作用于混凝土面层垂直方向的作用力分量可表述为式中,A为混凝土面层反射系数。......
2025-09-29

将前文的颗粒相模型应用到二维明渠恒定均匀流,考察模型在明渠水流中的适用性。表3-3Einstein和Chien和Wang和Qian部分试验组次的流动条件为了模拟上述明槽水流中的泥沙运动规律,应用前文的颗粒相动量方程式、能量方程式和本构关系式、式,液相紊动与颗粒作用关系采用式和式。考虑到表3-3中各组次的C0.1不超过10%,为计算方便,忽略动量方程和能量方程中的碰撞应力、脉动能碰撞传导通量。......
2025-09-29

应急大数据种类多,关系复杂。该混合时空数据模型将应急时空大数据抽象为数据集{时间,空间,事件},如图2.10所示。其中时间轴T为UTC时间,空间轴X为与突发事件相关的空间基础数据,存储形式为CGCS2000坐标系下的大地坐标,事件轴E是突发事件的相关数据,主要包括致灾因子、承灾体、孕灾环境、抗灾体等数据。将X及E投影到时间轴,可视为在某一时间节点上的快照片段数据,表达为该时刻发生事件涉及的空间区域以及应急数据。......
2025-09-29

同时,冲击波传入靶体,在径向产生压应力和应变,在切向产生拉应力与应变。由于混凝土靶体材料的抗拉强度远低于抗压强度,因此靶体首先在拉应力作用下发生断裂,形成径向裂纹。气体产物沿裂纹区扩散,导致裂纹进一步扩展,造成本体功能型硬目标结构爆裂毁伤。图6.33混凝土靶爆裂毁伤计算模型混凝土靶体中最终裂纹长度取决于高压气体产物膨胀,而爆燃压力直接取决于进入侵孔内活性材料的质量。......
2025-09-29
相关推荐