5.4.3.2杭州湾不恒定流及泥沙计算图5-73用平面二维泥沙数学模型计算三峡坝区泥沙浓度和泥沙淤积情况平面二维泥沙数学模型在计算三峡坝区泥沙浓度收敛过程 ;平面二维数学模型计算三峡坝区泥沙淤积时，比较沿程断面流量守恒情况图5-75杭州湾不恒定流水位、流速和泥沙浓度验证情况5.4.3.3葛洲坝三江上下游引航道的不恒定流验证图5-74杭州湾地理位置和计算区域示意图杭州湾位于钱塘江出海口，如图5-74所示，是一个强潮型河口。......
2023-06-22
模型验证：深槽水流和泥沙计算分析
【摘要】：图5-112中性物质在弯道中图 ，图 和图 连续排放的平均浓度验证图5-112中性物质在弯道中图 ，图 和图 连续排放的平均浓度验证图5-113试验深槽以及垂向计算网格示意图图5-113试验深槽以及垂向计算网格示意图图5-114计算深槽水流结果与Van Rijn 试验及Alfrink 计算结果比较5.5.5.3深槽水流、 泥沙计算验证图5-114计算深槽水流结果与Van Rijn 试验及Alfrink 计算结果比较5.5.5.3深槽水流、 泥沙计算验证Van Rijn 在进行了多组不同尺寸和流量的水流跨过深槽的水槽实验。
5.5.5.1 弯道水流计算验证
图5-110 实验弯道示意图 (单位:m)
为了研究弯道螺旋流对物质的混合过程，Chang(1971)对弯道上水流速度和中性物质浓度分布进行了测量，实验水槽(如图5-110)由两个90°弯道组成，弯道半径8.53m，弯道之间由4.27m 直水槽过渡，弯道进出口分别由长为2.13m 的直段过渡，弯道横断面为矩形，宽2.34m。进口平均流速为0.366m/s，平均水深为0.115m，水面比降S=0.00035。流速测量断面位置如图5-110中虚线所示。模型计算网格为354×24×22个，网格大小为0.1m 左右，计算时间步长0.1s。数值试验表明迭代计算1000步接近稳定。
模型验证了弯道13个测量断面上的流速，限于篇幅只列出第二弯道尾部 (PI/2)横断面的验证结果(图5-111)。可见，模型计算纵向流速和横向流速与实测值吻合较好，尤其是在弯道中部附近的流场计算精度相对较高。在弯道凹岸靠近自由面附近区域横向流速计算值和实测值偏离较大，主要是在该区域存在一个与主二次环流旋转方向相反的次生二次环流，而紊流模型不能够模拟次生二次环流。此外，河道边壁网格疏密和壁函数取值可能对边壁流场也有一定的影响。
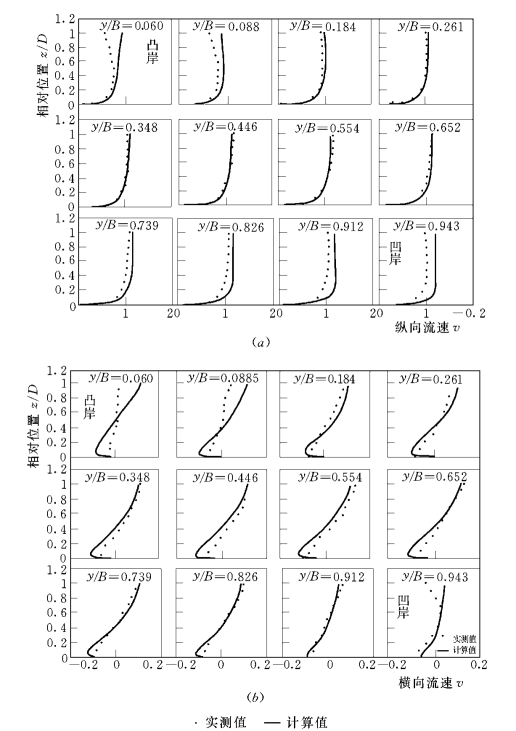
图5-111 PI/2断面沿主流和垂直主流方向流速沿水深分布
y—断面横向坐标;z—与河底距离;D—水深;B—宽度;
5.5.5.2 弯道输运和泥沙计算验证
Chang (1971)试验在第一个弯道进口的左、中、右分别设置中性物质排放点。试验在两弯道过渡段和第二个弯段上13个断面测量中性物质浓度。试验用中性物质密度与水相同且在输运过程中不发生降解，因此中性物质输运方程的源项取为0。对物质在第一个弯道进口中部、右和左岸排放，模型计算横断面三维浓度分布垂向平均值与实测资料对比如图5-112所示。对中部排放，计算值和实测值吻合较好，但在弯道凹岸有一定偏离，这可能是弯道螺旋流误差引起。两侧连续排放，采用S1断面上垂向平均浓度作为进口条件，得到垂向物质平均浓度计算值和对应实测值吻合较好。
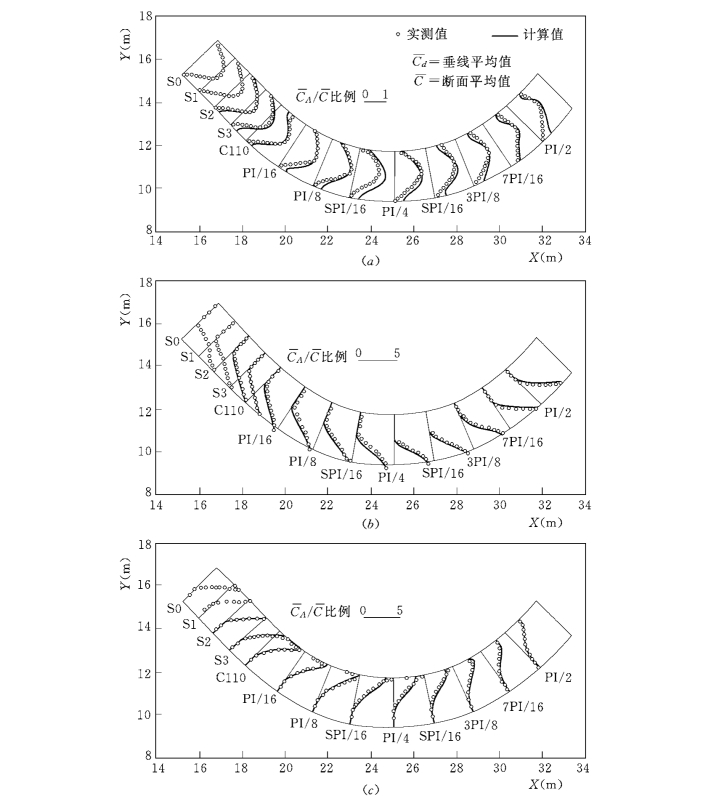
图5-112 中性物质在弯道中图 (a)，图 (b)和图 (c)连续排放的平均浓度验证
图5-113 试验深槽以及垂向计算网格示意图
图5-114 计算深槽水流结果与Van Rijn (1987)试验及Alfrink (1983)计算结果比较
5.5.5.3 深槽水流、 泥沙计算验证
Van Rijn (1987)在进行了多组不同尺寸和流量的水流跨过深槽的水槽实验。深槽几何尺寸见图5-113。试验进口平均流速为0.395m/s，水深为0.204m，床面泥沙平均高度为0.006m，有效的粗糙高度为0.02m。深槽水流测量位置如图5-113中标注。模型的计算网格为(180×12×22)，中间纵向立面计算网格分布如图5-113所示。试验测量了各个断面的纵向流速，紊动动能和切应力分布。同时，Alfrink (1983)对这一试验也进行了模拟计算，结果如图5-114 所示。同时，根据三维模型计算河床摩阻流速:U*=
摩阻流速与实测结果比较见图5-115。可见，本计算和试验流场资料以及他人的计算结果都比较吻合。对于泥沙计算的验证，仍选用Van Rijn (1987)深槽系列实验。深槽几何尺寸同前面，河床表面铺设的泥沙特征参数为:D50=0.16mm，D90=0.2mm。床沙厚为0.2m，进口悬沙输沙率为0.03 kg/sm，推移质输沙率为0.01kg/sm。
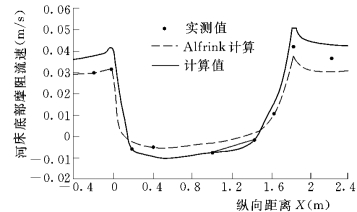
图5-115 模型计算深槽底部摩阻流速和实测资料等的验证比较
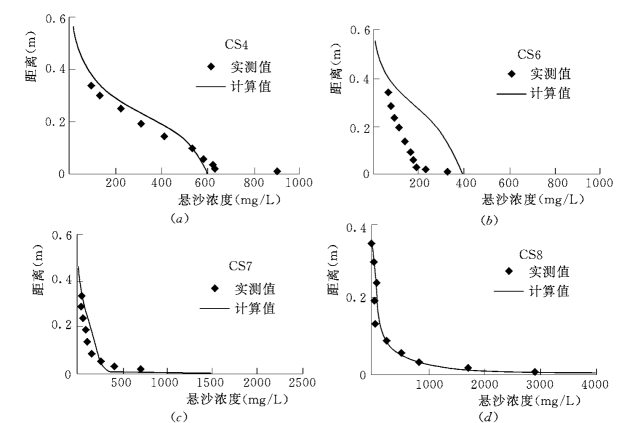
图5-116 模型计算泥沙浓度分布和Van Rijn (1987)实测资料的比较
泥沙浓度计算与实测的比较 (图5-116)可见，含沙量分布在深槽前后边坡和实测值吻合良好，而在深槽中部悬沙浓度计算值与实测值相差较大，误差达到50%左右。水流经过深槽时，由于断面增大、流速减小，河床发生淤积，不断的淤积沙洲随着过程的发展向下游传递;在深槽恢复正常水深后，由于流速减速加大，深槽后部的边坡发生一定冲刷。图5-117给出了在T=0，2，4，6，8，10，12，15h时计算地形的分布情况和T=15h Van Rijn 实测的地形资料及Van Rijn的立面二维模型计算的地形的对比。模型能模拟出深槽地形随时间的变化过程和实测地形比较吻合。
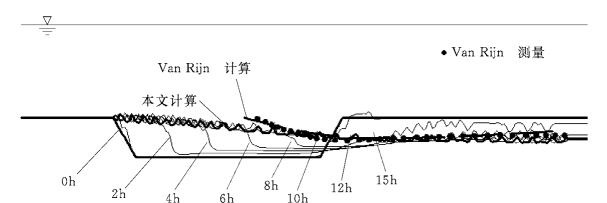
图5-117 模型计算河槽冲淤过程和Van Rijn (1987)实测和计算结果的比较
有关泥沙研究进展的文章
- 详细阅读
-
复式河槽水流泥沙特性分析和优化详细阅读
由于复式河槽滩地植被的覆盖，原本复杂的复式河槽水沙特性更为复杂。复式河槽随着流量增大、水位抬高，当水位超过滩地高程时洪水漫滩，产生一系列水流结构、水流阻力、泥沙输移和河床演变的复杂变化。这种游荡性河流断面形态呈现复式河槽的特点。为了保护堤防的安全，应采取保护岸滩的措施。岸滩种植植被，利用根系保护土壤，避免水土流失，起到固滩固岸的作用。......
2023-06-22
-
初步应用二维水流泥沙模型探究河道演变详细阅读
游荡型河道是多沙河流最基本的形态之一。最近，作者利用已建立的全动床、不恒定、不平衡和不均匀的水流泥沙数学模型对游荡河道的产生和变化进行了初步的计算研究。并且，在河道变化过程中，游荡河流的一些典型的特性得到展现。在天然河道演变中，控制节点通常是非常重要的因素。......
2023-06-22
- 详细阅读
-
大水深和小水深对水流泥沙输移的影响分析详细阅读
图2-1床沙质含沙量与无量纲单位水流功率参数的关系为了说明大水深河流和水深较小的实验室水槽中输沙能力的不同，图2-1点绘了床沙质含沙量与无量纲的单位水流功率参数的关系。小水深水槽试验和大水深河流雷诺数的差别达到两个数量级，这种差别必然会影响到水流阻力和与之相关的泥沙输移过程。图2-3的结果再次说明，由于实验室水槽的水深变化范围有限，依据实验室水槽资料建立的输沙关系，不能够代表大河流的输沙关系。......
2023-06-22
-
模型验证计算的优化方法详细阅读
模型用于待建工程计算前，应进行天然河道率定。最大输沙率计算值为0.16615kg/s，发生在7920s，沙峰试验值较计算值滞后。最大输沙率试验值与计算值之比1.69。验证计算结果见图9-25。......
2023-06-22
-
三维水流、泥沙数学模型的基本方程详细阅读
本节的全三维不恒定流和泥沙数学模型基本方程建立在平面正交曲线坐标和立面σ坐标系下:5.5.1.1水流运动基本方程连续方程平面ξ方向的动量方程连续方程平面ξ方向的动量方程平面η方向的动量方程平面η方向的动量方程垂线σ方向的动量方程垂线σ方向的动量方程动量方程式～式中DP1，DP2，DP3项分别为压力P=pa+ps+pd在ξ，η，σ方向上的梯度项，pa为水面处大气压强，ps为静水压强，pd为动水压强。......
2023-06-22
-
初步应用三维水流泥沙模型的优化方案详细阅读
在弯道段，在主流和二次环流作用下的水流含沙浓度平面分布表明，凸岸浓度明显高于凹岸。用三维模型研究了弯道上推移质运动。本算例水流计算时间步长0.1s，泥沙计算步长5.0s，泥沙粒径0.36mm。利用这一试验来对比和检验具有横向展宽和变形的模型计算结果的合理性。......
2023-06-22
相关推荐