三维水流、泥沙数学模型的基本方程

本节的全三维不恒定流和泥沙数学模型基本方程建立在平面正交曲线坐标和立面σ坐标系下:

5.5.1.1　水流运动基本方程

连续方程平面ξ方向的动量方程

连续方程平面ξ方向的动量方程

平面η方向的动量方程

平面η方向的动量方程

垂线σ方向的动量方程

垂线σ方向的动量方程

动量方程式(5-86)～式(5-88)中DP1，DP2，DP3项分别为压力P=pa+ps+pd在ξ，η，σ方向上的梯度项，pa为水面处大气压强，ps为静水压强，pd为动水压强。DF1，DF2，DF3分别为水流动量方程的扩散项，模型坐标系统下DP1，DP2，DP3，DF1，DF2，DF3的详细表达式见文献(黄国鲜，2006)，水流紊动粘性系数的表达式为:υt=Cμk 2/ε，k，ε分别为水流紊动动能和紊动动能耗散率，采用标准k～ε紊流模型求解水流紊动粘性系数，模型坐标系下k、ε方程具体形式见文献(黄国鲜，2006)。

5.5.1.2　泥沙运动基本方程

将泥沙运动分为推移质和悬移质，在计算中将非均匀泥沙按照粒径的大小分组，同组泥沙按照均匀沙处理，悬移质泥沙的基本方程是:

动量方程式(5-86)～式(5-88)中DP1，DP2，DP3项分别为压力P=pa+ps+pd在ξ，η，σ方向上的梯度项，pa为水面处大气压强，ps为静水压强，pd为动水压强。DF1，DF2，DF3分别为水流动量方程的扩散项，模型坐标系统下DP1，DP2，DP3，DF1，DF2，DF3的详细表达式见文献(黄国鲜，2006)，水流紊动粘性系数的表达式为:υt=Cμk 2/ε，k，ε分别为水流紊动动能和紊动动能耗散率，采用标准k～ε紊流模型求解水流紊动粘性系数，模型坐标系下k、ε方程具体形式见文献(黄国鲜，2006)。

5.5.1.2　泥沙运动基本方程

将泥沙运动分为推移质和悬移质，在计算中将非均匀泥沙按照粒径的大小分组，同组泥沙按照均匀沙处理，悬移质泥沙的基本方程是:

在推移质运动层δb范围内泥沙运动的连续方程为(Van Rijn，1987)

在推移质运动层δb范围内泥沙运动的连续方程为(Van Rijn，1987)

式中:p′为泥沙的空隙率;δb为推移质泥沙运动层厚度;sb为 推移质在δb内平均含沙浓度;Db-Eb为推移质和悬移质运动交界面上泥沙颗粒上扬和沉降引起的净通量;qbx和qby分别为推移质沿x，y 方向的单宽输沙率，qbx=αxqb、qby=αyqb，在河床床面坡度不大的情况下，重力对泥沙的作用可以忽略，推移质的运动强度和运动的路线由床面附近水流流速来决定，其计算公式为:

通常情况下天然弯道和分汊河道局部床面的纵横向坡度较大，推移质的运动强度和运动的路线不仅受到底部流速的影响，而且受到床面坡度的影响，采用Van Rijn (1993)的处理办法来考虑床面坡度对推移质的影响:

(1)床面纵横向坡度改变了泥沙颗粒临界起动切应力，对其修正的公式为

式中:p′为泥沙的空隙率;δb为推移质泥沙运动层厚度;sb为 推移质在δb内平均含沙浓度;Db-Eb为推移质和悬移质运动交界面上泥沙颗粒上扬和沉降引起的净通量;qbx和qby分别为推移质沿x，y 方向的单宽输沙率，qbx=αxqb、qby=αyqb，在河床床面坡度不大的情况下，重力对泥沙的作用可以忽略，推移质的运动强度和运动的路线由床面附近水流流速来决定，其计算公式为:

通常情况下天然弯道和分汊河道局部床面的纵横向坡度较大，推移质的运动强度和运动的路线不仅受到底部流速的影响，而且受到床面坡度的影响，采用Van Rijn (1993)的处理办法来考虑床面坡度对推移质的影响:

(1)床面纵横向坡度改变了泥沙颗粒临界起动切应力，对其修正的公式为

式中:kβ为纵向坡度影响系数，在顺坡时kβ=sin(φ-β)/sinφ，kβ＜1， 逆坡kβ=sin(φ+β)/sinφ，kβ＞1，β纵向坡度，φ 泥沙水下休止角;kγ横向坡度影响系数，kγ=cosγ(1-tan2γ/tan2φ)0.5，γ横向坡度。

这一公式对床面横向坡度大于水下休止角时不再适用。理论上由均匀非粘性沙冲积形成的河道床面坡度不会大于泥沙的水下休止角，但是泥沙介质的非均匀性、河岸边界岩石的分布、二次环流和其他因素的影响可能会使得河床的坡度大于泥沙颗粒的水下休止角，这里的近似处理办法为kγ=cosγ。根据Sheilds在平底河床计算结果，临界切应力τb，cr大小为:τb，cr=ρθcr(s-1)gD50，θcr为临界运动参数，可以根据Sheilds曲线进行分段曲线拟合得到。

(2)床面坡度对推移质输沙率影响的修正公式为

式中:kβ为纵向坡度影响系数，在顺坡时kβ=sin(φ-β)/sinφ，kβ＜1， 逆坡kβ=sin(φ+β)/sinφ，kβ＞1，β纵向坡度，φ 泥沙水下休止角;kγ横向坡度影响系数，kγ=cosγ(1-tan2γ/tan2φ)0.5，γ横向坡度。

这一公式对床面横向坡度大于水下休止角时不再适用。理论上由均匀非粘性沙冲积形成的河道床面坡度不会大于泥沙的水下休止角，但是泥沙介质的非均匀性、河岸边界岩石的分布、二次环流和其他因素的影响可能会使得河床的坡度大于泥沙颗粒的水下休止角，这里的近似处理办法为kγ=cosγ。根据Sheilds在平底河床计算结果，临界切应力τb，cr大小为:τb，cr=ρθcr(s-1)gD50，θcr为临界运动参数，可以根据Sheilds曲线进行分段曲线拟合得到。

(2)床面坡度对推移质输沙率影响的修正公式为

式中:αs=tanφ/cosβ(tanφ±tanβ)， 顺坡取 “-”，逆坡取 “+”;ub，n，ub，s分别为床面附近流速沿横向和纵向的分量;τb，cr泥沙起动临界剪切力;τb，ss 方向的床面剪切力;ε系数(其建议值为ε=1.5)。

式中:αs=tanφ/cosβ(tanφ±tanβ)， 顺坡取 “-”，逆坡取 “+”;ub，n，ub，s分别为床面附近流速沿横向和纵向的分量;τb，cr泥沙起动临界剪切力;τb，ss 方向的床面剪切力;ε系数(其建议值为ε=1.5)。

如果推移质输沙处于平衡状态，推移质单宽输沙率就等于推移质单宽输沙能力，qb=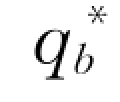 。 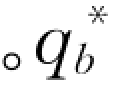可用Van Rijn公式计算:

如果推移质输沙处于平衡状态，推移质单宽输沙率就等于推移质单宽输沙能力，qb=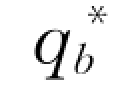 。 可用Van Rijn公式计算:

式中:D50为50%泥沙为细的泥沙粒径;T 无量纲剩余切应力T=(τ′b-τb，cr)/τb，cr;τ′b=αbτb;αb= (C/C′)2;C=18lg(12D/ks);C′=18lg(4D/D90);qb为推移质单宽输沙率;D为泥沙颗粒参数;τb，cr为临界切应力;τ′b为有效切应力;τb为床面切应力 (τb=ρu 2);C 为Chezy系数;C′为颗粒Chezy系数;ks为粗糙高度;D90为90%泥沙为细泥沙直径。

推移质泥沙的不平衡输运方程形式为

式中:D50为50%泥沙为细的泥沙粒径;T 无量纲剩余切应力T=(τ′b-τb，cr)/τb，cr;τ′b=αbτb;αb= (C/C′)2;C=18lg(12D/ks);C′=18lg(4D/D90);qb为推移质单宽输沙率;D为泥沙颗粒参数;τb，cr为临界切应力;τ′b为有效切应力;τb为床面切应力 (τb=ρu 2);C 为Chezy系数;C′为颗粒Chezy系数;ks为粗糙高度;D90为90%泥沙为细泥沙直径。

推移质泥沙的不平衡输运方程形式为

式中:Ls为推移质不平衡调整长度，根据Van Rijn(1987)实验研究Ls=3d50D 0.6T 0.9。在天然河道，它与泥沙颗粒跳跃长度相关，相当于Ls≈100D50。

将上述推移质运动方程转化为正交曲线坐标系统下，得到

式中:Ls为推移质不平衡调整长度，根据Van Rijn(1987)实验研究Ls=3d50D 0.6T 0.9。在天然河道，它与泥沙颗粒跳跃长度相关，相当于Ls≈100D50。

将上述推移质运动方程转化为正交曲线坐标系统下，得到(https://www.chuimin.cn)

求解本方程即可求出推移质输沙率空间分布。

5.5.1.3　河床变形方程

河床变形方程可用泥沙通量守恒法和非平衡输沙法来表示。通量守恒法的方程为

求解本方程即可求出推移质输沙率空间分布。

5.5.1.3　河床变形方程

河床变形方程可用泥沙通量守恒法和非平衡输沙法来表示。通量守恒法的方程为

qTξi，qTηi分别为ξ，η方向上全沙输沙率:

qTξi，qTηi分别为ξ，η方向上全沙输沙率:

式中:αξ，l，αη，l为床面坡度和底流流速分量对第l组推移质运动的影响系数。

当采用非平衡输沙的模式计算时，对推移质不平衡输运引起的河床变形可由式(5-98)确定。在假定推移质运动为均匀运动或无推移质运动情况下可以将方程进一步简化得出由悬移质不平衡输运引起的河床变形方程为

式中:αξ，l，αη，l为床面坡度和底流流速分量对第l组推移质运动的影响系数。

当采用非平衡输沙的模式计算时，对推移质不平衡输运引起的河床变形可由式(5-98)确定。在假定推移质运动为均匀运动或无推移质运动情况下可以将方程进一步简化得出由悬移质不平衡输运引起的河床变形方程为

在床面附近水流的垂向流速分量忽略不计的情况下，对悬移质非平衡输运引起的河床变形可由如下公式进行求解:

在床面附近水流的垂向流速分量忽略不计的情况下，对悬移质非平衡输运引起的河床变形可由如下公式进行求解:

此外，从悬沙上扬和下沉通量的角度也可以列出另一河床变形方程:

此外，从悬沙上扬和下沉通量的角度也可以列出另一河床变形方程:

sb，l为推移质和悬移质运动层边界上第l组悬沙平衡浓度，在实验室均匀沙输运计算中采用Van Rijn (1986)公式求解:

sb，l为推移质和悬移质运动层边界上第l组悬沙平衡浓度，在实验室均匀沙输运计算中采用Van Rijn (1986)公式求解:

式中:a为推移质运动高度;sb为推移质和悬移质运动层边界上悬沙平衡浓度。

在非均匀沙和天然河道泥沙输运计算中涉及到两个重要变量sb，l，sb，l，它们可利用平衡悬沙浓度分布并结合二维挟沙力公式和床面底部第一个有效网格节点上的计算悬沙浓度反求出来。

5.5.1.4　河岸冲刷与横向变形模拟方法

河道凸岸淤积主要是来自上游冲刷的粗泥沙和高洪水位情况下缓流淤积，二次环流横向输运作用也会加速弯道凸岸淤积，在三维模型中不必专门考虑弯道凸岸淤长过程。然而，对凹岸或顶冲点水下大幅度冲刷导致的失稳和坍落需要建立附加模型。

(1)河岸冲刷。边岸直接冲刷与水沙条件和边岸介质特性有关系，采用Osman(1988)模型来模拟河岸在水流直接冲刷下的后退过程，冲刷宽度按:

式中:a为推移质运动高度;sb为推移质和悬移质运动层边界上悬沙平衡浓度。

在非均匀沙和天然河道泥沙输运计算中涉及到两个重要变量sb，l，sb，l，它们可利用平衡悬沙浓度分布并结合二维挟沙力公式和床面底部第一个有效网格节点上的计算悬沙浓度反求出来。

5.5.1.4　河岸冲刷与横向变形模拟方法

河道凸岸淤积主要是来自上游冲刷的粗泥沙和高洪水位情况下缓流淤积，二次环流横向输运作用也会加速弯道凸岸淤积，在三维模型中不必专门考虑弯道凸岸淤长过程。然而，对凹岸或顶冲点水下大幅度冲刷导致的失稳和坍落需要建立附加模型。

(1)河岸冲刷。边岸直接冲刷与水沙条件和边岸介质特性有关系，采用Osman(1988)模型来模拟河岸在水流直接冲刷下的后退过程，冲刷宽度按:

式中:Ce为横向侵蚀系数，决定于河岸介质特性，Osman建议Ce=3.65×10-4;τ水流对河岸的切应力;τc河岸泥沙起动临界切应力，由Shields曲线查取，但由于河岸横向坡度较大，泥沙稳定性在重力分量作用下大为减弱，比平底河床更易起动，因此河岸泥沙临界切应力τc采用Van Rijn (1993)的修正方法。

考虑横向流速影响的河岸切应力为

式中:Ce为横向侵蚀系数，决定于河岸介质特性，Osman建议Ce=3.65×10-4;τ水流对河岸的切应力;τc河岸泥沙起动临界切应力，由Shields曲线查取，但由于河岸横向坡度较大，泥沙稳定性在重力分量作用下大为减弱，比平底河床更易起动，因此河岸泥沙临界切应力τc采用Van Rijn (1993)的修正方法。

考虑横向流速影响的河岸切应力为

式中:yp为临近边壁的有效节点到边壁的距离;up为相应点的流速;nb为河岸糙率;α1为经验系数，与水流流速与河岸夹角有关，当河岸附近流速指向河岸时α1取值要大，反之则小。

(2)水下边岸坍塌。河岸坍塌失稳机理非常复杂，准确模拟还具有一定困难。分别采用水下休止角和内摩擦角稳定方法来近似模拟水面上下河岸坍塌过程。河岸坍塌分水上和水下两种情况。对水下，根据休止角修正水下地形。休止角大小根据泥沙粒径和种类选择，一般介于31°～40°之间。水上河岸根据土体内摩擦角修改地形。干燥土体坍塌面角度一般接近垂直，为了简化计算将模型中露出水面河岸角度一般限制在70°～90°之间。水上和水下坡度稳定和坍塌过程判别和计算是一个试算过程，需要多次判别坍塌位置和地形修正，直到地形和河岸稳定为止。

(3)坍塌泥沙在河床附近分布。水下失稳和河岸坍塌泥沙在水动力学条件作用下如何在水下堆积受很多因素影响。为简化计算，假设失稳坍塌泥沙均匀分布在其下游侧一定范围内的水下节点上。根据计算的失稳和坍塌泥沙体积，按均匀或一定规则等量分摊在下游临近的水下节点上，修改水下地形后，作为新的冲淤计算起始河床。

式中:yp为临近边壁的有效节点到边壁的距离;up为相应点的流速;nb为河岸糙率;α1为经验系数，与水流流速与河岸夹角有关，当河岸附近流速指向河岸时α1取值要大，反之则小。

(2)水下边岸坍塌。河岸坍塌失稳机理非常复杂，准确模拟还具有一定困难。分别采用水下休止角和内摩擦角稳定方法来近似模拟水面上下河岸坍塌过程。河岸坍塌分水上和水下两种情况。对水下，根据休止角修正水下地形。休止角大小根据泥沙粒径和种类选择，一般介于31°～40°之间。水上河岸根据土体内摩擦角修改地形。干燥土体坍塌面角度一般接近垂直，为了简化计算将模型中露出水面河岸角度一般限制在70°～90°之间。水上和水下坡度稳定和坍塌过程判别和计算是一个试算过程，需要多次判别坍塌位置和地形修正，直到地形和河岸稳定为止。

(3)坍塌泥沙在河床附近分布。水下失稳和河岸坍塌泥沙在水动力学条件作用下如何在水下堆积受很多因素影响。为简化计算，假设失稳坍塌泥沙均匀分布在其下游侧一定范围内的水下节点上。根据计算的失稳和坍塌泥沙体积，按均匀或一定规则等量分摊在下游临近的水下节点上，修改水下地形后，作为新的冲淤计算起始河床。