在弯道段,在主流和二次环流作用下的水流含沙浓度平面分布表明,凸岸浓度明显高于凹岸。用三维模型研究了弯道上推移质运动。本算例水流计算时间步长0.1s,泥沙计算步长5.0s,泥沙粒径0.36mm。利用这一试验来对比和检验具有横向展宽和变形的模型计算结果的合理性。......
2023-06-22
游荡型河道是多沙河流最基本的形态之一。游荡河道中重要的次类是辨状河流(Braiding River),也是最复杂的河道流形态。黄河中游和下游河南河段都是以游荡河段为主要河型。游荡河道水浅、滩多、水流分散、滩槽变化频繁,泥沙淤积迅速,河道持续抬高,主流非常不稳定,整治这类河道具有很大困难。而且,由于河道变化复杂,水沙变化起伏大、过程快,受各种尺度相似要求的限制,实体模型试验也难以准确模拟。利用数学模型模拟游荡河道具有重要的科学和实用价值。最近,作者利用已建立的全动床、不恒定、不平衡和不均匀的水流泥沙数学模型对游荡河道的产生和变化进行了初步的计算研究。初步研究表明,本模型可以模拟游荡河道的产生和发展过程。并且,在河道变化过程中,游荡河流的一些典型的特性得到展现。特别重要的是,计算证实在含沙量相对不高、过程相对简单的水沙作用下,游荡河型最终会向单一弯曲型转化,这对认识上游水库调控下的黄河下游治理具有一定的意义。这里介绍的仅是一个初步结果,作者认为这是一个值得进一步深入研究方向。
数学模型以DIVAST 水流模型为基础,利用作者建立的不恒定、不平衡泥沙数学模型对前者进行补充。数学模型的挟沙能力仍按式 (5-36)。该式是最原始的张瑞瑾公式,但它与通常黄河数学模型采用公式的重要差别在于其水沙因子U 3/g Hω 的指数不小于1。这一点具有重要的物理意义,在后面将要讨论。模型模拟不均匀泥沙。考虑泥沙浓度对沉降速度影响:
![]()
根据王兆印等(钱宁,1989)的研究,取指数k=7.0。
模拟游荡型辫状河流的关键在于模拟变动河床动水边界问题和模型对小水深区的准确计算。基于DIVAST 模型中干湿网格计算方法,考虑到河床变形的影响进行了修改。在动边界计算中使用的床面粗糙高度和阻力计算粗糙高度相同,都取为沙粒阻力高度,它和床沙粒径相关:
![]()
其中D65是河床表面65%泥沙粒径。在干湿网格计算中,判断干网格重新淹没的尺度取为常数(Δ≈10~50mm)。在模型中,河道阻力系数(谢才系数)按公式:
![]()
计算。另外,计算冲刷时的挟沙力时需要考虑泥沙起动条件,公式中的水沙因子U 3/g Hω修改为U 2(U-Uc)/g Hω,其中Uc为泥沙起动流速。
5.4.5.1 简单河道
简单河道算例的情况是:河宽2.7km,长33.4km,河道横断面均匀,纵向坡降0.233‰(相当于黄河中游花园口段的坡降)。床沙和悬沙级配按1959年花园口—辛寨河段的实测资料(图5-101)。初始条件下,床沙按给定级配均匀铺设。进口水流和泥沙过程均用,流量和泥沙浓度分别是2500m3/s和45kg/m3,下游出口水位不变。泥沙分成6组,各组泥沙的平均粒径分别是0.0038,0.0074,0.0169,0.0368,0.0736 和0.1694mm,水温按20℃。河床泥沙分成HT=0.4m,HM=1.0m 和HL=10m 三层。计算采用30×372 个90m 的正方网格,计算时间步长ΔT=12s和24s分别模拟水流和泥沙冲淤。
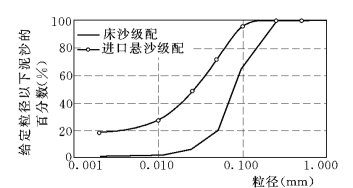
图5-101 黄河花园口1959年9月悬沙及花园口—辛寨河段实测泥沙级配资料
为加速冲淤变化进程,在进口附近设置一道800m 长垂直丁坝作为扰动控制接点。在天然河道演变中,控制节点通常是非常重要的因素。图5-102显示河床泥沙冲淤厚度的变化情况。初期,由于丁坝扰动出现不均用局部冲刷和淤积,然后冲淤过程不断向下游发展。在12h左右形成浅滩和深水交错的河槽,但浅滩都出于水下。进一步随着深槽冲刷,浅滩逐步露出水面,形成辫状发展的游荡河流。但是,由于过程中水沙条件没有发生大的起伏,多汊分流状态难以长期维持,逐步形成强势发展的单一主槽和次槽萎缩现象。单一主槽继续以弯曲蜿蜒方式发展,最后形成完全单一的弯曲河型。当然,如果在过程中水沙条件发生较大变化,多汊型游荡河型将会更长期维持下去。由计算河道演变过程可见,在黄河小浪底水库控制下,下游河道的水沙条件趋于简单,加上泥沙淤积的减少,今后河南河段也可能在一定时期内向弯曲河型发展。

图5-102 模型模拟从简单河道通过游荡向弯曲河型变化的过程(图中灰度深浅代表冲淤厚度m)
在模型中,床沙级配变化对河道冲淤的影响很大,相应床沙级配变化过程的合理性需要考虑。图5-103是与图5-102相应的时序过程中河床表面泥沙粗细的变化情况。可见,冲刷部位与床沙粗化、淤积部位与细化相对应。主槽床沙明显比滩地泥沙粗很多,一些盲肠河汊床沙甚至出现极细的现象。这都是合理的结果。
值得指出的是,本模型是平面二维的。弯道等变化的重要驱动因素——二次流等不能得到反映,所以结果是近似的。但是,对于类似黄河下游河道变化的问题,通常水深比较浅,二次流作用相对较小,河道变化过程主要是泥沙堆积与主槽冲刷之间消长关系的变化而产生。所以,二维模型结果仍然具有参考意义。当然,对类似长江河道变化的问题,依靠平面二维模型模拟的结果可能就会较大偏离实际。

图5-103 河道演变过程中床沙粗细和流场的变化过程
5.4.5.2 花园口—辛寨河段
在上述研究基础上,进一步模拟了黄河下游花园口至辛寨河段的河道情况。本河段由很多宽窄相间的河段组成,河道左右摆动很大,是典型的游荡河段。对这一河段洪水和泥沙冲淤计算都具有很大难度。计算结果还是非常不成熟的内容,主要是想通过下面的介绍反映数学模型在辫状河流模拟方面的结果。数学模型对于黄河演变问题的比较可靠的模拟,研究还有很远距离。
河段长35.2km,最宽的断面大6km。模型计算依据1959年9月11日在本河段测量的35个断面而生成的地形资料(见图5 104)。模型进口水沙条件见图5 105,是1959年汛后的实际过程,辛寨断面的水位也是当时的实测水位;床沙和进口泥沙级配与前例相同。计算采用100m 的正方形网格,水流泥沙计算的时间不长分别是8s和32s。
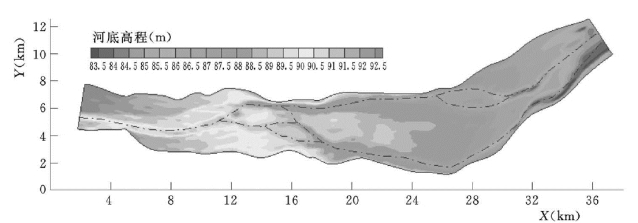
图5-104 1959年9月11日黄河花园口—新寨河段的地形 (模型初始地形)
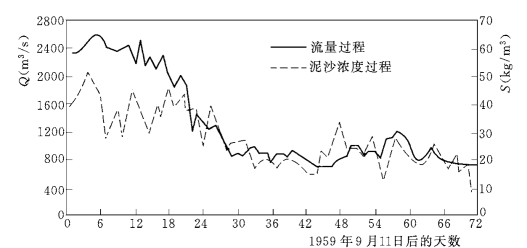
图5-105 1959年9月11日后2.5 月时间里花园口断面的水沙过程
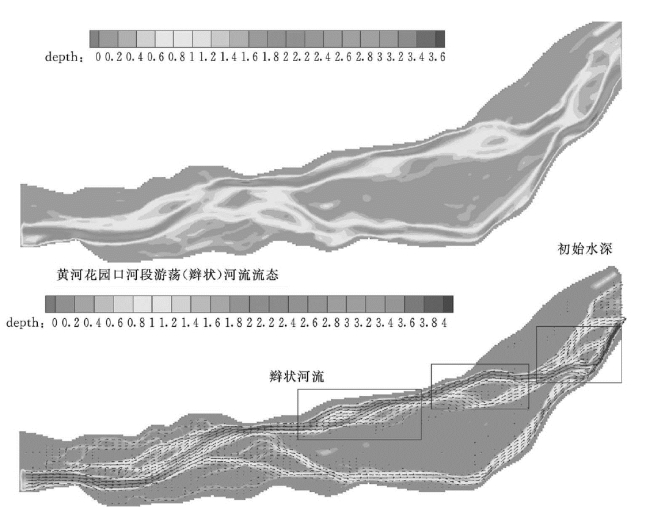
图5-106 黄河花园口—辛寨河段河道演变过程的模拟结果
图5-106是计算给出的初始和经过过20多天冲淤之后本河段的河道变化情况(用水深表示)。可见,在冲淤过程中,本河段辫状河流发展十分活跃,便装河流形态是河道演变的重要台阶。
上述模拟结果和1959年汛后本河段实测的河道变化过程还有很大距离。但是,通过计算结果至少显示,目前的不恒定不平衡泥沙数学模型可以在复杂的河道演变过程的模拟计算中发挥作用。通过进一步的努力,数学模型可以为今后类似黄河下游河道整治工程布置等重要问题研究提供新的工具。
有关泥沙研究进展的文章

在弯道段,在主流和二次环流作用下的水流含沙浓度平面分布表明,凸岸浓度明显高于凹岸。用三维模型研究了弯道上推移质运动。本算例水流计算时间步长0.1s,泥沙计算步长5.0s,泥沙粒径0.36mm。利用这一试验来对比和检验具有横向展宽和变形的模型计算结果的合理性。......
2023-06-22

5.4.3.2杭州湾不恒定流及泥沙计算图5-73用平面二维泥沙数学模型计算三峡坝区泥沙浓度和泥沙淤积情况平面二维泥沙数学模型在计算三峡坝区泥沙浓度收敛过程 ;平面二维数学模型计算三峡坝区泥沙淤积时,比较沿程断面流量守恒情况图5-75杭州湾不恒定流水位、流速和泥沙浓度验证情况5.4.3.3葛洲坝三江上下游引航道的不恒定流验证图5-74杭州湾地理位置和计算区域示意图杭州湾位于钱塘江出海口,如图5-74所示,是一个强潮型河口。......
2023-06-22

在三峡论证期间,确定了三峡工程采用五级船闸结合垂直升船机方案解决三峡枢纽通航。图5-87二维泥沙数学模型计算结果显示,三峡运用后期引航道口门段存在严重的淤积但是,将升船机和船闸同时包括在引航道内又导致船闸充水波动对升船机的影响和引航道内部泥沙淤积和清淤等问题。......
2023-06-22

平面二维水流泥沙数学模型有关泥沙部分的主要理论和方法在前面已经有所介绍。数学模型控制方程由水深平均下的浅水方程和泥沙输运方程构成。在小含沙量的条件下,在水中运动的各组粒径的泥沙之间可以认为是相互独立的,在输运方程中可以单独考虑分组泥沙浓度。有关分组挟沙能力或冲刷函数、恢复饱和系数的计算方法已在前面介绍。但是,不恒定模型计算时段较小,处理起来难度相对较小。......
2023-06-22

图5-112中性物质在弯道中图 ,图 和图 连续排放的平均浓度验证图5-112中性物质在弯道中图 ,图 和图 连续排放的平均浓度验证图5-113试验深槽以及垂向计算网格示意图图5-113试验深槽以及垂向计算网格示意图图5-114计算深槽水流结果与Van Rijn 试验及Alfrink 计算结果比较5.5.5.3深槽水流、 泥沙计算验证图5-114计算深槽水流结果与Van Rijn 试验及Alfrink 计算结果比较5.5.5.3深槽水流、 泥沙计算验证Van Rijn 在进行了多组不同尺寸和流量的水流跨过深槽的水槽实验。......
2023-06-22

对SF6断路器近区故障开断能力进行数值分析,首先应建立开断过程动态数学模型,因为电弧、灭弧室、喷口和动静触头等具有轴对称形状,且以灭弧室中轴线为其对称轴,所建数学模型在空间上为二维轴对称。采用K-ε两方程模型来描述湍流效应。......
2023-07-02

河道泥沙运动研究成果较多,有针对黄河中下游干流的数学模型及应用系统,但受限于实测资料和高含沙水流的特殊规律,动力学模型仅限于在干流的应用,无法向泥沙源区沟道扩展。在借鉴已有研究成果的基础上,完成流域水沙全过程模拟仍然需要重力侵蚀、无断面资料沟道及有断面资料河道的水沙输移等方面的动力学模型研究。......
2023-06-22

本节的全三维不恒定流和泥沙数学模型基本方程建立在平面正交曲线坐标和立面σ坐标系下:5.5.1.1水流运动基本方程连续方程平面ξ方向的动量方程连续方程平面ξ方向的动量方程平面η方向的动量方程平面η方向的动量方程垂线σ方向的动量方程垂线σ方向的动量方程动量方程式~式中DP1,DP2,DP3项分别为压力P=pa+ps+pd在ξ,η,σ方向上的梯度项,pa为水面处大气压强,ps为静水压强,pd为动水压强。......
2023-06-22
相关推荐