图9-23Wireshark在OC和RC中捕获MSRO消息序列在已建立的平台中，我们考虑了实际的应用程序场景和复杂性实验设置，并建立了生成简单业务需求的业务生成器。对于所提的GES，我们预先设定了可调节比重φ、β和γ分别为50%、33%和33%，以避免模拟环境下实验过于复杂。如图9-25所示，相较于其他方案，GES可以有效地提高资源占用率，特别是当网络负载很重的时候。......
2025-09-29
二维水流泥沙模型验证的优化方法
【摘要】：5.4.3.2杭州湾不恒定流及泥沙计算图5-73用平面二维泥沙数学模型计算三峡坝区泥沙浓度和泥沙淤积情况平面二维泥沙数学模型在计算三峡坝区泥沙浓度收敛过程 ;平面二维数学模型计算三峡坝区泥沙淤积时，比较沿程断面流量守恒情况图5-75杭州湾不恒定流水位、流速和泥沙浓度验证情况5.4.3.3葛洲坝三江上下游引航道的不恒定流验证图5-74杭州湾地理位置和计算区域示意图杭州湾位于钱塘江出海口，如图5-74所示，是一个强潮型河口。
这里介绍的验证成果主要针对作者较早的模型 (周建军，1988)，长期以来，作者对该模型进行了较多的验证。其中水流计算程序的验证包括了天然资料，实体模型资料及水槽不恒定流实验资料;泥沙计算程序则主要通过与实体模型进行验证。
5.4.3.1 模型稳定性和守恒性验证
在各种水流条件下模型稳定、收敛性和输运物质守恒性是数值模拟的关键，经过大量试算表明，模型水流计算在柯朗数Cr=(U± g H)ΔT/Δx=0～3.0，糙率n≥0.014时都能处于稳定状态，泥沙计算在对流柯朗数C′r=UΔT/Δx ≤1.0时都是稳定的。
图5-73(a)是计算三峡坝区(坝区情况后面介绍)泥沙输运过程中的情况。对上游给定的台阶变化输沙过程，下游经过一定时间后都可达到稳定过程。表明本模型对泥沙计算具有较好的稳定和收敛性。关于水流计算的质量守恒性，图5-73(b)给出在三峡坝区计算过程中，当计算收敛时，从上游到下游各个断面积分流量的分布情况，可见其偏差仅在1%以内，在图中，流量的沿程脉动是由岸线不规则，边线处流量积分不准确造成的。关于输运量的守恒性，曾进行过沉降速度为0时，进出口浓度的比较，其偏差也在1%以内。
关于模型的灵敏性，通过对糙率变化进行过试验，在三峡近坝区约18km 的河道上，当流量Q=56700m3/s时，水位为145.0m 时，当糙率n=0.017±10%时，上游水位变化仅在10cm 左右，在初期上下游水位仅差60cm，水位变化引起的水深及流速变化完全可以忽略，对泥沙运动也没有影响，其它如扩散系数、时间步长等在一定的范围内变化时，也是可以容许的。初始床沙级配对初期计算影响较大，但初期泥沙呈单向淤积，其影响很快消失。因此可认为模型性能满足工程要求。
5.4.3.2 杭州湾不恒定流及泥沙计算
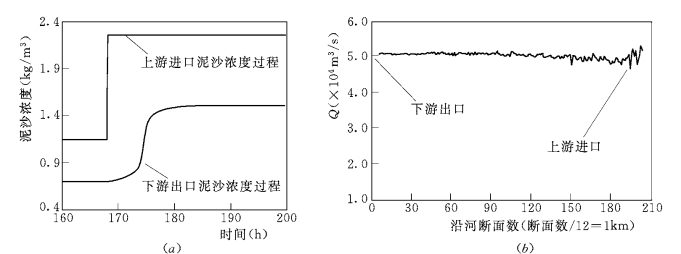
图5-73 用平面二维泥沙数学模型计算三峡坝区泥沙浓度和泥沙淤积情况
(a)平面二维泥沙数学模型在计算三峡坝区泥沙浓度收敛过程 (上游进口泥沙浓度改变后，经10～20h出口断面浓度趋于恒定);(b)平面二维数学模型计算三峡坝区泥沙淤积时，比较沿程断面流量守恒情况
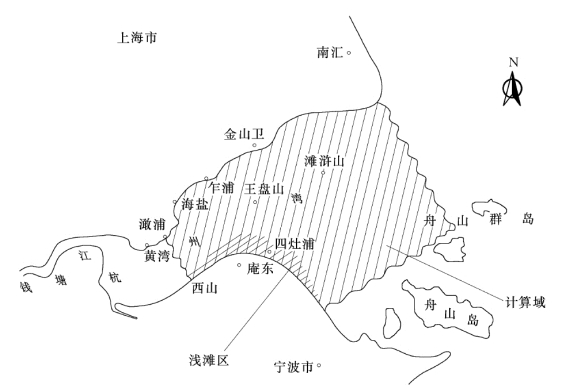
图5-74 杭州湾地理位置和计算区域示意图
杭州湾位于钱塘江出海口，如图5-74所示，是一个强潮型河口。河口在平面上呈收敛形，湾口宽约100km，收缩至澉浦宽约20km，北岸乍浦、金山一带为深水区，岸边地形比较复杂，南岸西山至龙山一带是大片的沙滩，随潮流的涨落出没。河口水流及潮差变化比较剧烈，外海波进入湾口后，由于平面地形收缩引起一定的反射，潮差急剧增大，湾口年平均潮差为2～3m，至澉浦时，增加至5.5m 左右。杭州湾泥沙主要来自外海，从长江口向南飘移而至，主要是粉沙为主，中径在0.02～0.04mm 之间，在沉降过程中有一定的絮凝。由于计算范围不大，泥沙分选不严重，可以按均匀沙来处理，河口内泥沙易于起动，搬运频繁，泥沙运动相当复杂。水流的挟沙能力公式是根据浙江河口海岸研究所提供的经验公式计算:
验证采用浙江河口海岸研究所2025年6月29日～7月31日对杭州湾多测站同步水流及含沙量的测量资料。计算范围如图5-74所示，x 方向最大宽度106km，y 方向最大宽度为70km，为了适应地形，坐标x，y 方向并不与地球经纬度方向一致，全域基本糙率为0.013，考虑了局部阻力变化，在沙滩和水深变化急剧的地方，实际糙率依然较大，有的地方可以达到0.03左右，北岸为垂直岸边界，用边界对称点法模拟，南岸有大片沙滩，用动边界处理，东南方向以及澉浦进口为水位边界。计算网格Δx=Δy=2000m，时间步长为ΔT=600s，计算节点总数约为2000个。由水位、流速验证结果 (图5-75)可见，无论潮位还是流速过程都与实测资料基本吻合，部分点在高水位时较实际过程落后30min左右。与水位相比，流速过程的计算值与实测值的误差要大一些，这是由于流速局部地形变化较大，数值计算受网格大小及计算精度的限制，较难准确模拟出局部地形影响。各测站含沙量计算值和实测值的比较，虽然精度低，但考虑到潮流输沙问题的复杂性，计算过程在趋势上还是能够反映实际问题。
图5-75 杭州湾不恒定流水位、流速和泥沙浓度验证情况
5.4.3.3 葛洲坝三江上下游引航道的不恒定流验证
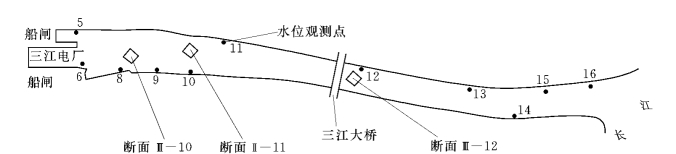
图5-76 三江下游引航道水位及流速测点位置示意图
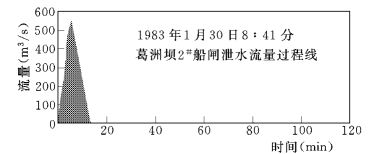
图5-77 验证计算过程中葛洲坝船闸泄水流量条件(https://www.chuimin.cn)
前面的二维水流模型在三峡引航道隔流堤规划、双线船闸取水口位置选取和船闸取水错峰时间等研究中大量应用。之前先选择与研究问题相关的葛洲坝三江引航道上下游的不恒定流实测数据来对模型进行必要的验证。图5 76是三江下游引航道及实测水位和流速位置分布示意图，在图5-77给定的引航道泄水流量作用下，三江引航道产生连续的波动过程，下游出口水位采取长江相应时间的水位资料。图5-78是各个测点计算水位过程与实测过程的比较，计算与实测的各点水位变化完全一致，其中包括下游由于波动变形产生的次波都能很好的吻合。对断面Ⅲ—10、Ⅲ—11 和Ⅲ—12 的流速变化过程验证情况，各点的计算流速过程与实测资料吻合非常好。
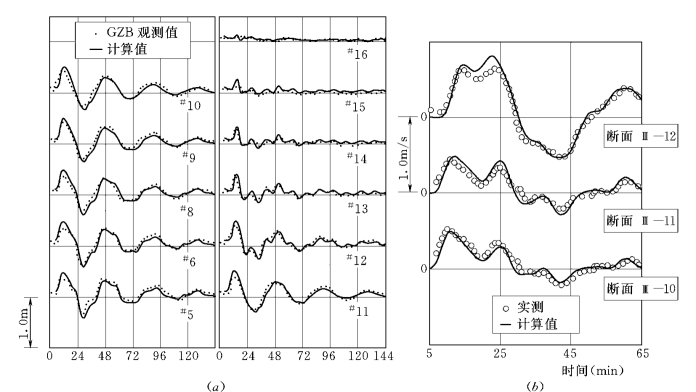
图5-78 计算水位流速过程与原型观测资料比较
5.4.3.4 三峡近坝段河道泥沙淤积验证
三峡坝区模拟河段(图5-79)上起腊肉洞，下至三斗坪，全长17.5km。本段河谷宽阔，洪水河宽一般为600～700m，最大洪水河宽在三斗坪附近，达到1400余m，建库以后，坝前段最大河宽达到3000m 以上。近坝区河段河床为岩石、乱石及卵石组成，河道深泓高程变化剧烈，平均深泓高程10～30m，最低处高程-32.8m，最高处深泓达50m，河底起伏不平，存在倒坡，局部微地形对流态与流速分布具有十分强烈影响(图5-80)。
清华大学在室内对上述河段进行了模型试验，数学模型和模型试验同步开展，边界条件完全相同。水文系列条件采用长科院数学模型计算的1961～2025年自然系列加上1954～2025年洪水，10年系列循环进行。根据“分期蓄水”的运用原则，在水库建成后初期10年，坝前水位按照156m—135m—140m 进行调度，汛期防洪限制水位为135m，自第11年起，坝前水位按照175m—145m—155m 进行调度，防洪限制水位145m。考虑到非汛期几乎没有泥沙到达三峡坝前，在流量流速较大时，才会引起床面冲淤变化。因此，在模型试验和数学模型计算中，主要模拟汛期流量大于15000m3/s以上时段的泥沙冲淤变化。
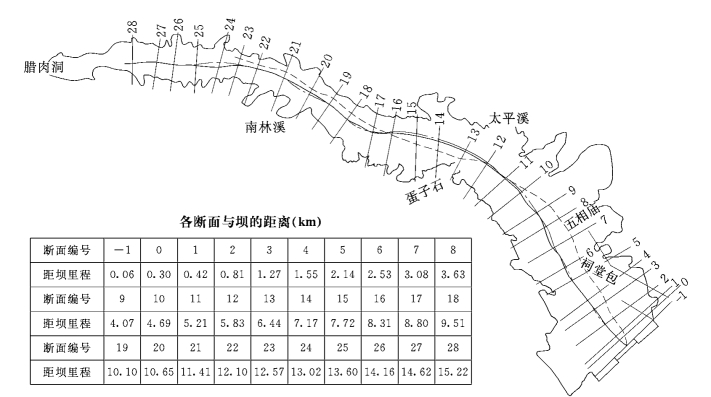
图5-79 三峡坝区河段数学模型计算范围示意图
图5-80 三峡近坝段 (坝前8.5km 左右)范围卫星照片 (2025年蓄水后)
在运行前30年，因水深大、流速小，计算河道进出口水位相差较小，糙率对计算结果影响较小，取为n=0.02。后期河道接近冲积河道，取下游荆江河段糙率n=0.016～0.018。计算中平面动量扩散与泥沙扩散系数相等，采用Elder公式:εm=εs=5.92HU。模型挟沙能力解数与韩其为的一维数学模型采用的一致，即:Ks=0.247，m0=0.92。淤积物干容重近似取γ0=1300kg/m3。另外，在计算中没有考虑淤积泥沙密实过程。由于坝区泥沙较细，各级泥沙的沉降速度按Stokes公式计算，计算中水温按夏季平均水温T=25℃。采用Δx=Δy=75.0m 的正方形网格，全域一共布置约为7000个有效网格点。计算采用与物理模型相同的阶梯型水沙概化条件。水流、泥沙浓度及河床变形计算可以在一个时段里分别进行，水流计算采用ΔT=10s，泥沙计算采用ΔT=30～50s的时间步长，河床变形计算时间步长根据河床变形厚度控制，要求期间冲淤厚度不超过5mm。
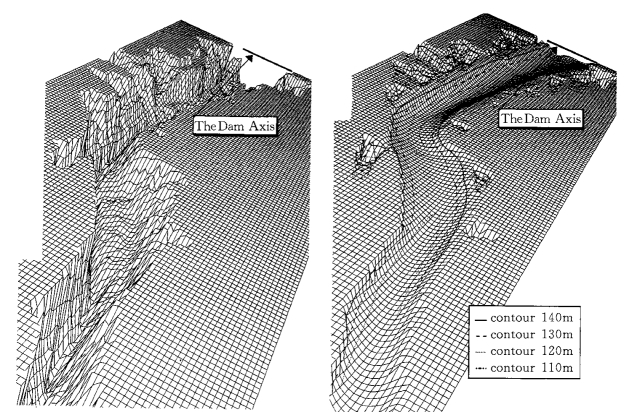
图5-81 初始和水库运行76年后模型计算近坝区地形比较
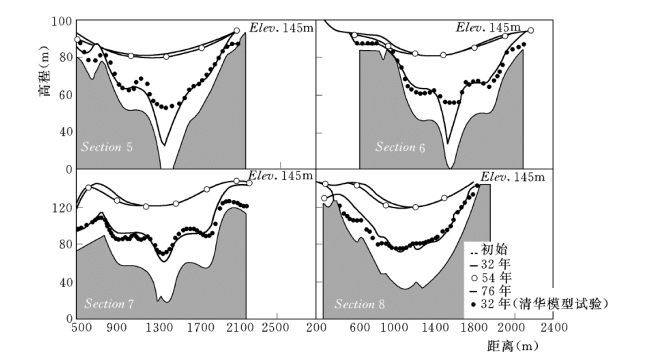
图5-82 数学模型计算河道淤积断面，第32年结果与清华大学实体模型试验比较
图5-81是初始和水库运行76年后模型计算的近坝区地形分布对比，可以看出最初河道地形十分复杂，河谷较为窄深。在水库雍水作用下，河道出现累积淤积，河道变得宽浅并呈现出冲积河道形态。 图5-82给出了第32年时数学模型计算的各个断面与清华大学实体模型得到的相应断面的比较，计算结果总体上和实体模型试验结果一致，只是在具有较明显深槽部位有较大差异，这可能与深槽部位具有复杂三维水沙结构有关，二维模型还不能够准确地模拟出来。图5-83给出水库运行后近坝段累积淤积随时间段的变化过程的计算结果与实体物理模型试验以及一维模型计算结果的比较。可见二维模型与实体模型试验值吻合较好。此外，还给出了运行32年后在坝前水位145m 时回水曲线下各断面的过水面积沿程变化(图5-84)，过水断面计算和试验值吻合很好。
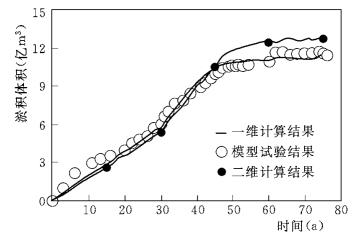
图5-83 三峡水库运行76年过程中，计算坝区河段泥沙累积淤积过程的模型验证
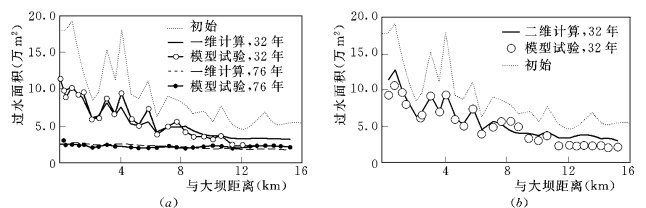
图5-84 汛限水位145m 以下的计算过水面积和实体模型试验结果比较
相关文章
- 详细阅读
-
验证颗粒流模型的可靠性详细阅读
Bagnold 最先在同心圆筒间进行悬浮石蜡颗粒的剪切试验，颗粒直径为1.32mm，比重为1.05g/cm3;以水、酒精和甘油混合成不同比重的溶液来平衡颗粒的自重，当浓度C≥0.3 时，颗粒碰撞作用占优势，Bagnold实验用来验证本文的理论结果。当浓度C 从0.04 增加到0.35 时，两者之比从10减小到0.1，该浓度范围内的颗粒碰撞应力和脉动应力都很重要。......
2025-09-29
- 详细阅读
-
建立操作机构仿真模型的优化方法详细阅读
通过ADAMS软件提供的图形接口模块，将三维实体造型软件UG中建立的机构三维模型导入到ADAMS软件中的。考虑到所关心的问题和仿真的方便，对操作机构作适当简化后，用ADAMS软件包建模。约束关系的添加要充分考虑实际操作机构中可能存在的约束，遗漏任何一个约束关系都会严重影响到输出结果。3）仿真过程的控制 在ADAMS软件中，为了实现对仿真过程的控制，需要添加传感器来控制仿真过程的自动终止。......
2025-09-29
-
数值模型验证：探索真实性详细阅读
Ccond=0.000 1时小流量和设计流量工况下离心泵扬程随有效空化余量变化的非定常数值计算结果与试验结果的比较如图2.6所示。表2.2NPSHc计算值与试验结果的比较在本书的离心泵空化流动数值模拟中，质量输运空化模型的凝结项经验系数取0.000 1进行数值计算。图2.7列出了小流量下NPSHa=1.0m和设计流量下NPSHa=1.6m时，3个不同凝结项经验系数所对应的叶轮内空泡体积率分布。......
2025-09-29
-
验证网络性能的方法详细阅读
图9-1实验测试平台和演示器设置基于测试平台，我们在软件定义的C-RoFN中实验性地设计并验证了MSO的服务。功能请求消息负责定期查询OF-BVOS关于当前状态的监视。此外，在选择目的地之后，CSO策略仅考虑光网络资源并以最小跳数计算路径。GES部分地扩展了BBU中的负载均衡和光网络中的平均跳跃性能，并将它们明显地转化为整体资源利用率的提高和路径配置响应的增强。图9-3算法性能比较......
2025-09-29
-
网络性能验证的方法和步骤详细阅读
表9-2评估参数的值在下文中，评估中使用的性能指标是平均节能。从图9-16可以看出，当网络负载低于50 Mbit时，MH-DBA的平均节能率为0.85，而3M-DBA的平均节能率为0.28。当网络负载超过300 Mbit时，控制器节能率开始趋于平稳。图9-17丢包率与平均节能率当吞吐量趋于稳定时，我们总结出能量效率的结果。随着网络负载的增加，两种机制的节能率降低，这是因为系统触发睡眠机制的概率会随着负载的增加而降低。......
2025-09-29
-
明渠水流模型在实际应用中的优势与挑战详细阅读
将前文的颗粒相模型应用到二维明渠恒定均匀流，考察模型在明渠水流中的适用性。表3-3Einstein和Chien和Wang和Qian部分试验组次的流动条件为了模拟上述明槽水流中的泥沙运动规律，应用前文的颗粒相动量方程式、能量方程式和本构关系式、式，液相紊动与颗粒作用关系采用式和式。考虑到表3-3中各组次的C0.1不超过10%，为计算方便，忽略动量方程和能量方程中的碰撞应力、脉动能碰撞传导通量。......
2025-09-29
相关推荐