图12-9流域水沙资源优化配置数学模型框图流域水沙资源优化配置的方法采用多目标规划法,其优化配置模型目前宜采用多目标线性规划数学模型。根据流域水沙资源多目标优化配置原理,联合水资源优化配置,以泥沙资源优化配置为重点,结合专家调查和层次分析数学方法,构造综合目标函数,深入研究水沙资源优化配置的各种方式,确定配置约束条件,建立流域水沙资源多目标优化配置数学模型。......
2023-06-23
5.2.1.1 基本方程
数学模型的基本方程包括不恒定流方程、不平衡输沙方程、河床冲淤方程和其他辅助方程。明渠一维不恒定水流计算采用圣维南方程,泥沙运动包括悬移质和推移质运动,悬移质运动采用一维不平衡输沙方程计算。数学模型所涉及的方程如下所列,即
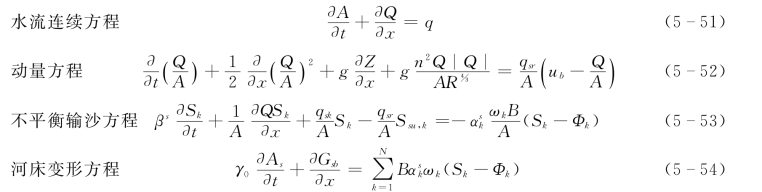
式中:A 为河道过水断面面积;Q 为流量;q=qsr-qsk为单位长度区间汇流和出流量,m3/(s·m);qsr为入流量;qsk为出流量;Z 为水位;B 为断面宽度;x 为距离;t为时间;g 为重力加速度;ub为入流在x 方向的投影速度;R 为渠道的水力半径;n 为渠道的糙率系数;Sk为断面平均分组泥沙浓度;ωk为分组泥沙颗粒的沉降速度;Φk为水流挟沙能力;As为河道冲淤面积;Gsb为推移质输沙率;Ssu,k为随入流入河道的泥沙浓度;N 为泥沙分组数;αsk为泥沙恢复饱和系数。
关于分组水流挟沙能力,在较早的模型中采用冲刷函数的概念:
![]()
Φk是第k 组泥沙的冲刷函数;φk=Pkφ 是分组挟沙能力:模型。

关于床沙级配计算,采用分层储存的计算方法。根据原始床沙级配资料和可冲层厚度,将床沙划分为若干层。表层床沙的级配计算采用下列方法:

模型考虑了推移质,设推移质量的泥沙分组为N+1至M 共Nb=M-N 组,总输沙率:
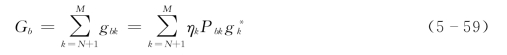
式中: 为第k 组泥沙单独存在时的推移质输沙率,可以根据梅叶—彼得公式计算;ηk为推移质量的组间影响系数,ηk =Dk/D50。
为第k 组泥沙单独存在时的推移质输沙率,可以根据梅叶—彼得公式计算;ηk为推移质量的组间影响系数,ηk =Dk/D50。
虽然推移质计算按平衡输沙方法,但模型中考虑了推移质的传递时间影响。
5.2.1.2 模型参数计算方法
在式(5-53)、式(5-54)中,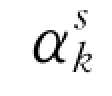 为河道的泥沙综合恢复饱和系数,它与河道断面形态,冲淤状态及水流泥沙运动参数有关,βs为反映断面流速和输沙不均匀分布的系数。它们分别由式(5-27)和式(5-28)确定。
为河道的泥沙综合恢复饱和系数,它与河道断面形态,冲淤状态及水流泥沙运动参数有关,βs为反映断面流速和输沙不均匀分布的系数。它们分别由式(5-27)和式(5-28)确定。
关于断面冲淤分配的计算方法。严格讲,一维数学模型不可能准确计算泥沙冲淤在横断面上的分布。但是,河道断面冲淤的分配又是模型必需的环节,它在很大程度上影响水库冲淤结果。特别是对水库模型,淤积置放在滩地或主槽甚至可在本质上影响水库的动力特性。然而,迄今所有一维数学模型都采用经验方法修改河道断面,比如冲刷和淤积都按湿周分布,或者淤积沿断面均匀分布、冲刷只影响主槽等。经验方法给数学模型带来了较大的任意性。特别是在河道冲淤交替情况下,经验方法甚至人工主观决定了所塑造的断面形态。作者等(Zhou和Lin,1998)依据流管积分和恢复饱和系数的理论体系,提出了冲淤沿断面分配的理论公式(5-31)从理论上定性解决了这一问题。
对水库淤积变化过程,糙率及其变化是非常重要的参数。本模型采用根据淤积厚度与天然突体的关系插值的方法。假设天然河道床面突体高度δb,天然河道糙率n0和冲积床面糙率nf,根据沿断面上各点的淤积厚度,按线性插值可以给出该点不同时候的糙率:
![]()
全断面平均糙率为
![]()
其中,d p 是断面湿周微分,χ=∫d p 为断面湿周长度,天然突体尺度可根据资料率定选取,模型中取δb=10m。由于三峡水库淤积量较大,突体尺度影响的持续时间不长。与韩其为和黄煜龄采用的以淤积面积为参数直接插值相比,本方法给出的过渡期糙率相对要小些,而且对于变动回水区和水库岸边(高水位地方)淤积较少的地方,天然阻力单元的作用可以长期自动地保留下来。
泥沙的沉降速度可按张瑞瑾公式计算:
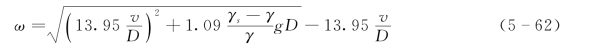

图5-23 根据张瑞瑾等 (Zhang et al,1993)挟沙力系数和指数 (假设m=0.92后)得到月的挟沙力系数
其中,泥沙比重γs=2.65。模型中水下淤积泥沙干容重按1325kg/m3计算。数学模型中也可选择水利部规范规定的沉降速度计算方法。对于不同粗细的泥沙,式 (5-61)和水利部规范的公式有一定的差异。部归入系数,则由式 (5-36)得到张瑞瑾公式在所有指标U 3/g Hω 变化范围 (如图5-23所示),挟沙力系数都小于韩其为等(1988)采用的系数,韩其为等采用的系数是图5-23的最大值。在三峡等水库泥沙淤积计算中,偏大的挟沙力系数会导致计算泥沙淤积数量偏少。三峡水库采用上述系数需要认真研究和检验。最有效的方法是结合三峡水库实测淤积加以检验。
挟沙能力按张瑞瑾公式计算,其系数和指数按韩其为取为KS=0.246,m=0.92。对于在三峡水库的计算,采用这些系数可以保证模型计算成果与中国水利水电科学研究院 (韩其为等,1988)和长江科学院 (黄煜龄等,1988)的成果一致。但是,根据前面关于全沙挟沙力系数和指数的讨论,如果将张瑞瑾公式的指数取为0.92,将其他变数影响全
5.2.1.3 三峡水库一维数学模型的计算条件
模型重要的应用是在三峡水库水流及泥沙淤积计算。三峡水库一维数学模型采用了与中国水利水电科学研究院等完全相同的计算断面。断面资料包括干流三斗坪至朱洋溪长735km 的165个断面、嘉陵江18个断面和乌江14个断面。
水文资料与长江科学院的10年序列相同。即由1961~1970年实际水沙系列资料为典型系列年,10年概化为800时段,按10年一个周期循环。
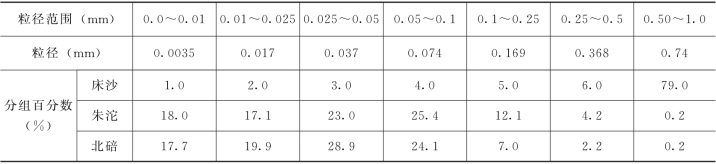
计算只考虑了悬移质。悬移质进入水库的泥沙级配按朱沱、北碚两站的进库资料。悬移质的级配是年内和多年不变的。计算将泥沙分成7组。每组泥沙的粒径范围,床沙级配和进库泥沙级配如表5-1所示。其中床沙级配比较任意,但是对淤积水库而言,原始床沙级配对成果的影响非常小。目前,三峡水库泥沙数学模型都采用了与表5-1类似的级配资料,级配资料都没有随过程变化而变化。
分组泥沙的平均粒径年根据算术平均和几何平均的平均值计算,即
![]()
这样计算的平均粒径小于直接用算术平均得到的数值。
天然糙率和水库淤积平衡糙率资料和韩其为等(1988)的资料完全一样。
表5-1 三峡水库入库泥沙和床沙级配
5.2.1.4 数值计算方法
数学模型不恒定水流计算采用Preissmann四点隐格式。该计算方法可以直接计算不恒定流动,具有很好的稳定性和精度。与常用的推水面线方法相比,该方法可以很好地适应缓流和急流及其过渡计算,对河道中峡谷段可能出现的急流能很好的模拟。Preissmann格式在文献中有详细介绍,在此不拟赘述。
对不恒定情况,不平衡输沙方程直接采用隐式迎风差分方法,计算公式为

上面的差分方法在质量守恒和稳定性方面比较好,也基本上可以达到计算要求的精度。在计算精度要求高的时候,也可以通过分步法首先计算方程的对流部分,采用样条插值等方法(Holly,1977)。剩下的源汇项可以用式 (5-64)计算 (除去其中与对流项相关的部分)。
对恒定情况,不平衡输沙方程求解采用韩其为的局部解析方法,即
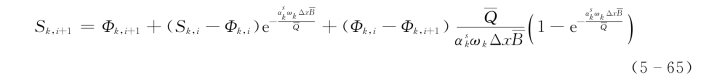
求解其他方程,如河床变形方程等都比较简单,可以直接利用差分法给出。
有关泥沙研究进展的文章

图12-9流域水沙资源优化配置数学模型框图流域水沙资源优化配置的方法采用多目标规划法,其优化配置模型目前宜采用多目标线性规划数学模型。根据流域水沙资源多目标优化配置原理,联合水资源优化配置,以泥沙资源优化配置为重点,结合专家调查和层次分析数学方法,构造综合目标函数,深入研究水沙资源优化配置的各种方式,确定配置约束条件,建立流域水沙资源多目标优化配置数学模型。......
2023-06-23

依照文化和旅游部公布的数据,2018年国内旅游人数55.39亿人次,中国公民出境旅游人数14972万人次。与此相关的另外一项“2018年中国公民赴欧洲旅游大数据报告”,则显示在这些旅游活动中,“文化旅游”的占比高居榜首。从一网站的欧洲游景点门票销量看,“文化旅游”范畴的艺术人文景点占了绝大多数。构成这个组合词的两个词语的原生语义,自然直接影响到我们对“文化旅游”这个组合词的基本判断。......
2023-11-17

图13-24异重流潜入位置变化过程表13-7水库运用初期1~5年库区输沙计算结果图13-24异重流潜入位置变化过程表13-7水库运用初期1~5年库区输沙计算结果在相同的水沙条件及边界条件下进行的小浪底库区实体模型试验结果表明,距坝67km 以下库段总淤积量为29.44 亿m3,若淤积物干容重γ0=1.15t/m3,则淤积量为33.8亿t。......
2023-06-23

式中 vs——风力发电机的启动风速,m/s;vc——风力发电机的截止风速,m/s;vi——第i时刻的风速,i=1,2,…,n,且vs≤vi,vi+1≤vc;Pi——风速功率曲线对应风速为vi时风力发电机输出的功率,kW。......
2023-06-23

一个典型的图像目标识别系统如图1-1所示,主要由图像增强与变换、图像分割、图像描述、分类决策四部分构成。其鲜明的特点是输入和输出的都是图像。高层处理一般是基于知识进行推理和证实的,涉及图像或图像区域的理解,以及执行与视觉相关的识别函数[8]。图1-1 图像目标识别系统的基本框架图图像目标识别技术是延伸和扩展人的视觉功能的方式和方法,其实信息技术整体都可以认为是扩展人的信息器官功能的技术。......
2023-06-28

计算结果从定性上与相应河段模型试验结果一致,定量上略有差别。小浪底水库调节后,出库沙量大幅度下降,特别是大于0.025m 的中、粗沙大部分被拦截在库区。......
2023-06-23
相关推荐