作者在前面关于挟沙能力公式结构形式分析时，曾经直接拟合张瑞瑾等原始公式，得到张瑞瑾公式的指数应该为式 。......
2023-06-22
挟沙能力的计算方法
【摘要】：悬沙和床沙粒径悬殊范围更大。现在有关数学模型分组挟沙力计算方法和下面的讨论都是相当近似的。
泥沙运动力学关于河流挟沙能力的研究(钱宁等，1983)，不能完全满足泥沙数学模型的需求。基于试验和实际资料得到的挟沙能力的理论和经验公式都是针对均匀沙或全沙;同时，多数挟沙力公式都是基于床沙质概念，忽略冲泻质部分。当河道处于基本平衡时，冲泻质的确不会发挥太大的作用。但是，在研究水库淤积和河床演变时，冲泻质泥沙是非常重要的部分。比如，三峡水库在几十年淤积过程中，水库平均淤积比例将达到60%左右，而天然情况下三峡上下游河道床沙质的比例只在15%～25%以内。黄河主槽泥沙冲淤主要是床沙质，但黄河下游每年淤积泥沙中冲泻质比例很大，边滩等淤积对河道变化关系重大。所以，数学模型需要模拟全沙(韩其为，1980)。另外，在通常情况下，即使最简化的天然河流泥沙冲淤计算都需要考虑不均匀沙问题，一般需要对泥沙级配进行分组。
5.1.7.1 全沙挟沙力计算公式
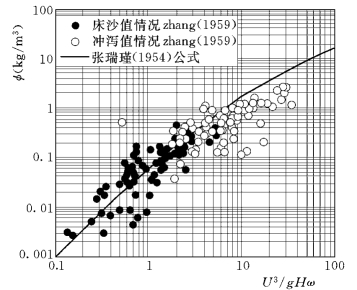
图5-20 张瑞瑾 (1959)包含冲泻质与床沙质情况的比较
根据定义，挟沙能力是平衡条件下水流挟带泥沙的浓度。对均匀泥沙或相当于均匀泥沙，可采用Einstein(1950)，Bagnold(1966)，Engelund和Hansen(1967)，Arkers和White(1973)，Yang(1979)和Van Rijn(1984)等公式。这些公式多是针对床沙质的，国内泥沙数学模型多倾向于采用基于Velikanov(1954)重力理论的张瑞瑾(1959)公式。由图5-20的长江实测资料显示，张瑞瑾公式可以包括冲泻质计算。
张瑞瑾公式的经验指数和系数是数学模型计算的重要问题。韩其为(1980)在其三峡等数学模型计算中取K=0.247，m=0.92，黄河数学模型计算多采用K=0.45，m=0.74(吴保生和龙毓骞，1993)。实际上，根据张瑞瑾和谢鉴衡(Zhang和Xie，1993)的研究，这些指数和系数是随指标U 3/gHω 变化变量:
变化规律如图5-21所示。为便于不均匀分组沙挟沙力公式的理论推导，采用没有指数的张瑞瑾公式在理论上可以与包括Bagnold (1966)等能量理论得到的公式形式相协调:
根据张瑞瑾和谢鉴衡(Zhang和Xie，1993)挟沙力指数和系数关系，可得到一个综合挟沙力系数:
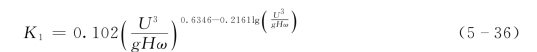
其变化规律见图5-21。这样得到的挟沙关系和原始的张瑞瑾公式几乎完全一样 (如图5-20所示)。同时，式 (5-36)也相当于挟沙能力公式系数保持常数，而指数是一个变量:
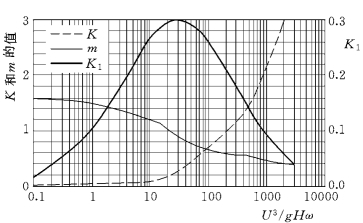
图5-21 张瑞瑾公式的系数和指数，以及本节建议的综合指数
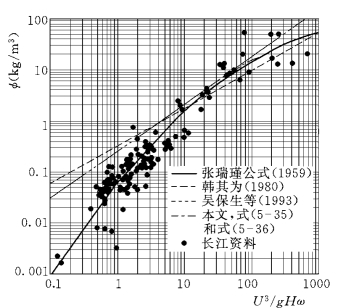
图5-22 按公式 (5-37)和系数K1计算挟沙力与张瑞瑾等公式比较
式(5-37)表明，在通常情况下(U 3/g Hω＜1000)，张瑞瑾公式的指数应大于1。这一定性指标具有明确的物理意义。
5.1.7.2 分组挟沙力计算方法
冲积河流泥沙粒径变化范围很大。对河流和水库泥沙计算，最细和最粗泥沙粒径一般会相差百倍以上，沉降速度相差上千倍。悬沙和床沙粒径悬殊范围更大。数学模型必须考虑不均匀沙或分组泥沙挟沙能力计算。但是，迄今基于理论或试验的经验分组挟沙力公式不存在。特别是在不平衡情况下，分组挟沙力的计算方法更是一个没有解决的问题。现在有关数学模型分组挟沙力计算方法和下面的讨论都是相当近似的。
根据Bagnold(1966)的能量概念，水流输运全部不均匀沙所做的功应该为
式中:q为单宽流量;φi为分组挟沙力;Usi为分组泥沙运动速度，一般可取Usi=U。
上述输沙功应该是由水流能量τU 来提供。上述Bagnold输沙功的概念同样适用于某一粒径当量的全沙，所以:
式中:ωe为不均匀沙的当量沉速;Φ 为全沙挟沙力;φ 为粒径无关量。
式(5-39)表明，在不同粒径泥沙分组之间，存在一个不随粒径变化的可交换量，定义为输沙不变量:
对于一个给定的泥沙输运状况，有理由假设水流将能量(或输沙不变量)首先用于输运已悬浮在水中的泥沙，剩余的输沙不变量可以用于冲刷。根据概念，水流输运已悬浮泥沙消耗的输沙不变量应该是:
如果E＞φ=∑φi，水流显然不能提供足够能量以悬浮全部泥沙，考虑到水流可提供的最大输沙不变量不能超过φ，所以:
如果φs＜φ， 并且河床表面能够提供相应的泥沙，水流还会进一步冲刷。水流用于冲刷的输沙不变量相应可表示为
因此，式(5-42)和式(5-43)得到了悬浮泥沙和进一步冲刷泥沙的输沙不变量φs 和φe。
对于悬浮泥沙部分，每个分组得到的输沙不变量应该正比于实际输运泥沙所消耗的输沙不变量ωisi，所以:
由式(5-42)与式(5-35)，可得比例系数k=min(φ，E)/E=Φ(ωs)min[S/Φ(ωs)，1]/S，其中S=∑si，Φ(ωs)是针对沉速ωs=∑Piωi的挟沙力，Pi=si/S。所以，悬浮泥沙的分组挟沙力可以表示为
对用于冲刷的输沙不变量，分配到每个分组的比例应该和床面有效可冲的泥沙成比例，即与河床表面有效泥沙级配成比例。所以，用于冲刷的挟沙力可以表示为
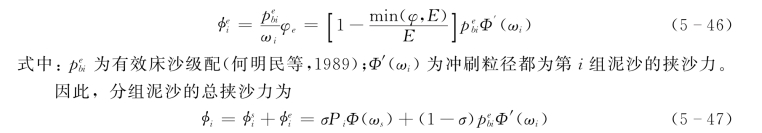
其中，权重系数σ=min[S/Φ(ωs)，1]。这就是不均匀泥沙在不平衡条件下的分组挟沙力计算公式。
在计算冲刷挟沙力时，用式(5-35)是不全面的。Φ′(ωi)需要考虑泥沙的起动条件，只有超过启动流速的泥沙才能被冲刷，所以式(5-35)修改为:
式中:Uci为分组泥沙的起动流速。
有效床沙级配受多方面因素的影响。首先，在水体中剩余的用于冲刷的能量沿水深全面分布，而冲刷泥沙可悬浮的高度是有限的，泥沙不能被悬浮到的地方的冲刷能量不能利用于冲刷泥沙，所以，用于冲刷的有效输沙不变量应该与冲刷泥沙的悬浮高度成比例。另外，河床粗泥沙对细沙的隐蔽和粗沙自身的暴露作用都影响泥沙在床面的受力，河床表面泥沙受水流拖拽力的有效作用大小和床面剪切力的作用面积关系很大。
泥沙平均悬浮高度可根据平衡情况下泥沙的平均悬浮高度确定。根据Lane和Kalinske(1941)建议的悬沙浓度分布公式，可得
其中zi=ωi/κU*，是悬浮指标。泥沙隐蔽与暴露作用，可通过引入隐蔽函数ηi来反映，建议采用吴伟民等(Wu et al，2000)根据不同粒径泥沙突出高度的概率分析所得到公式。Karim(1998)认为作用与不同粒径泥沙的有效拖拽力应该与泥沙在河床表投影的面积成比例，由泥沙面积级配和体积级配的关系可得
综合上述因素，可以得到有效床沙级配的表达式为
其中Pbi是河床表面泥沙级配，Di是泥沙粒径。由式 (5-50)可见，有效床沙级配不仅仅是床沙多少的概念，它还包括了水流对床沙的有效作用力，不同粗细的被冲刷泥沙有效利用水体中用于冲刷的输沙不变量等。
有关泥沙研究进展的文章
- 详细阅读
-
潮流和波浪对沙的剥蚀能力详细阅读
我国河口海岸多为粉沙和淤泥所覆盖，在风浪和潮流的共同作用下，泥沙极易悬浮和输移。该地区的挟沙能力与风浪和潮流的能量有关。波浪能量的损耗可近似认为与其本身能量成正比。如果用R1和R2分别表示波浪和潮流在单位时间内用以悬浮泥沙所消耗的能量，则根据前述可以写出式中:β2和α0均为系数。......
2023-06-22
-
非均匀沙分组输沙能力优化详细阅读
近年来泥沙数学模型要求不仅要能够计算沿程冲淤和总含沙量沿程变化，还要能够计算悬沙与床沙的级配组成及其变化。为此，就必须建立非均匀沙分组输沙能力的计算方法。何明民和韩其为在研究非均匀悬移质不平衡输沙时引进了输沙能力级配的概念，认为一般条件下，输沙能力级配不仅取决于床沙级配，而且还与含沙量级配有关。并且证明，在明显淤积条件下，淤积物级配即为有效床沙级配，含沙量级配即为输沙能力级配。......
2023-06-22
-
沙画教学对儿童美术能力的发展有何意义详细阅读
而儿童沙画教学就是让孩子在玩沙子的过程中，发现自己的潜能、创造力、天性等。儿童沙画教学的一个主要特点是强调有故事内容、情节的融入。（二）沙画教学促进了儿童美术与多媒体技术的融合儿童沙画艺术的特点主要体现在利用多媒体技术传播。在儿童沙画教学中采用的象征形式，其内容往往包含着超自然的、异想天开的成分，既源于生活又具有创新性，与传统的绘画方式和格局，扩展儿童美术空间的表达。......
2023-10-31
-
岔巴沟流域产沙计算方法简析详细阅读
6.6.1.2模拟计算的准备工作1.子流域、河网及坡面的划分在进行模拟计算前，首先利用数字流域平台将岔巴沟流域划分为8个单元子流域，如图6-31所示。......
2023-06-22
-
儿童沙画教学实践：提升小学生审美能力详细阅读
沙画的这种强有力的表现形式被广大观众所喜爱，并为广泛传承。沙画教学进入中小学美术课堂已是大势所趋。通过沙画教学资源，学生可以潜移默化地受到教育的影响。沙画产业的发展促进了小学美术教育的发展，同时也增加了小学美术课堂的趣味性，促进了小学美术的课程改革。沙画与美术教育的结合将对中小学生的美术素养、动手能力方面产生重要的作用。......
2023-10-31
-
混凝土结构设计计算方法：承载能力极限状态详细阅读
公路桥涵承载能力极限状态是对应于桥涵及其构件达到最大承载能力或出现不适于继续承载的变形或变位的状态。公路桥涵的持久状态设计按承载能力极限状态的要求，对构件进行承载力及稳定计算，必要时还应对结构的倾覆和滑移进行验算。进行承载能力极限状态计算时，作用(或荷载)的效应应采用其组合设计值；结构材料性能采用其强度设计值。......
2023-09-19
- 详细阅读
相关推荐