实验室如果不能充分利用能力验证所给出的相关信息,而仅关注其结果的满意与否,那么实验室参加能力验证的价值将非常有限。能力验证结果的利用,会涉及实验室所有层级的人员,从一般技术人员到最高管理层。质量管理人员应参与能力验证结果的利用,尤其是对连续能力验证计划结果的利用。最高管理层不一定要熟悉能力验证的具体运作,但要正确理解能力验证的作用,以避免错误的利用能力验证结果。......
2023-06-29
5.1.6.1 与解析解比较
与解析解比较包括简单情况下,清水冲刷和单向淤积情况,主要论证两个问题:①理论分析的出发点,即边界条件式(5-8)的正确与合理性;②由理论恢复饱和系数计算结果与解析解的一致性。Hjelmfelt和Lenau(1970)、侯晖昌 (1964)和张启舜 (1980)的解析解将用于比较和检验。
图5-8是采用边界条件式(5-8)计算的冲淤过程。数值解与解析解基本一致。但是,若淤积过程采用第一类边界条件,则数值解将出现浓度倒置现象,这不符合泥沙运动实际情况;相反,若冲刷过程采用第二边界条件,则泥沙浓度恢复过程大幅度减缓,这是否正确在后面将结合实验资料进一步论证。
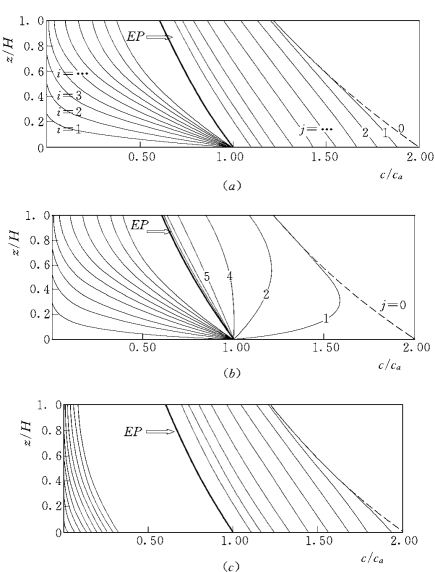
图5-8 由解析解与三维数值解给出的冲刷 (EP 线以左)和淤积过程 (EP 线以右)
(a)冲刷 (侯晖昌1964)和淤积 (张启舜1980)解析解;(b)按第一类边界条件的三维数值解;(c)按第二类边界条件用三维模型 (Lin 和Falconer,1997)计算的冲淤过程
(①图中:i 和j 表示剖面与进口的距离。对冲刷x = 0.025i 2Uh/κU*;对淤积x =0.30j 2Uh/κU*; ②计算条件:R=ω/6κU*=0.5,U=1.0m/s,h=1.0m;③EP 线是冲淤平衡的浓度剖面。)
对于水深平均的泥沙浓度过程,图5-9给出了用式(5-15)确定恢复饱和系数在完全均匀恒定流的条件下,由不平衡输沙方程数值计算的浓度恢复过程,并与有关解析解进行比较。可见,数值计算结果和解析解比较吻合。但是,在冲刷条件下,数值计算结果比解析解恢复饱和稍慢,式 (5-15)确定的恢复饱和系数还略偏小。如果采用韩其为(1980)建议的冲刷和淤积情况的恢复饱和系数 (分别是1.0和0.25),泥沙浓度恢复的速率将更慢(图5-9中虚线结果),与解析解偏离很大。
5.1.6.2 与室内试验结果比较
为检验理论恢复饱和系数正确性,试验室资料检验是重要的环节。在下面检验中,计算底部泥沙浓度一般采用Van Rijn (1984)的床面层泥沙浓度公式:
![]()
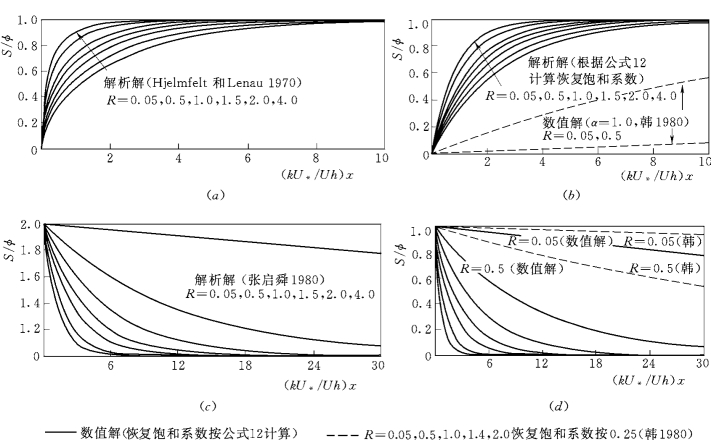
图5-9 恒定均匀流,计算泥沙浓度与解析解 (Hjelmfelt和Lenau 1970,张启舜1980)比较
(a)、(b)清水冲刷;(c)、(d)单向淤积
(虚线结果为按韩其为 (1980)恢复饱和系数 (冲刷α=1.0;淤积α=0.25)的计算结果。)
由于水槽试验一般为恒定均匀流,在这样条件下,不平衡输沙方程的解具有下面的简单形式:
![]()
所以,检验浓度分布等结果的唯一目的是检验恢复饱和系数的正确性。在上述公式中,cae是平衡条件下的底部泥沙浓度,D50是泥沙中径;T*= (τb-τb,cr)/τb,cr;D*=D50[(s-1)g/υ2]0.3333;s=ρs/ρ;τb是底部剪切力;τb,cr临界是底部剪切力;ρs,ρ是泥沙和水体的密度;υ是水体运动粘滞系数。
1.与张启舜试验比较
张启舜(1962)用60m 水槽试验模拟清水冲刷。试验条件:进口浓度C0=0,U=0.664m/s,H=0.114m,J=1.24‰,U*=0.0372m/s,a=0.02H,D50=0.06mm,D90=0.1mm,T=25℃ (水温)。图5-10 是测量立面浓度分布与Hjelmfelt 和Lenau(1970)理论解比较,可见第一类边界条件下,理论与试验结果非常吻合。对平均泥沙浓度恢复过程,不平衡输沙方程的解析式 (5-33)及解析解 (Hjelmfelt和Lenau,1970)都与试验资料吻合良好(如图5-11所示)。
2.与Van Rijn (1986)深槽试验比较
Van Rijn(1986)在水槽中进行了如图5-12所示的深槽冲淤试验。深槽比均匀水深0.39m均匀加深0.175m,进口流速0.51m/s,床面泥沙D50=0.16m(ω=0.013m/s)和D90=0.2mm,床面粗糙高度和谢才系数分别为ks=0.025 和C=19log(12H/ks)。周建军(Zhou,1998)采用三维数学模型计算,其中水流模型是基于k-ε 模型的紊流模型。由图5-13可见,按本节提出的河床边界条件,完全可以得到和试验结果相近的断面泥沙分布规律。
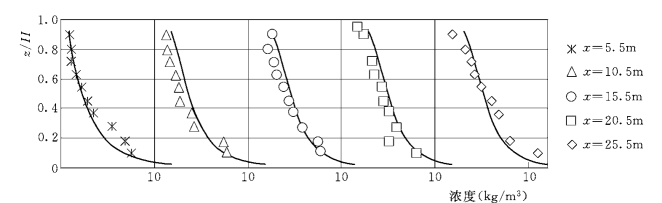
图5-10 张启舜水槽试验浓度分布与理论解(Hjelmfelt和Lenau,1970)比较

图5-11 方程 (5-33)数值解、解析解和张启舜 (1962)试验实测浓度分布的比较
3.与DHL试验比较
荷兰Delft水力学实验室(DHL)的试验(Van Rijn,1985)也模拟清水冲刷。试验条件为:C0=0,H =0.25m,U=0.67m/s,D50=0.23mm,D90=0.32mm;悬沙实测粒径0.20mm,相应沉降速度ω=0.022m/s(9℃水温)。数值计算取参考浓度高度取a=0.05H。图5-14和图5-15表明计算垂向浓度和水深平均浓度与试验结果都较好吻合,其中式(5-33)计算较解析解更接近试验数据。

图5-12 深槽纵剖面图 (单位:m)
4.与Van Rijn (1985)试验比较
Van Rijn(1985)在DHL进行了大型室内水槽试验。用长50m、试验宽1.55m 大型水槽铺设D50=0.22mm 泥沙模拟清水冲刷。试验水深约1m,平均水流速度1~2.8m/s,坡度0.25‰~0.5‰,水温15~20℃,共7组试验。每组2~4个断面实测浓度。各组试验和方程式(5-33)计算结果虽有偏差,但综合看是可以接受的(如图5-16所示)。
5.与张启舜不均匀沙试验比较
张启舜对相对均匀沙清水冲刷试验外,还在相同水槽进行不均匀沙清水冲刷试验。水流条件:Q=0.0319m3/s,H=0.133m,J=1.22‰。由于泥沙不均匀,计算采用一维数学模型,计算将床沙分成5 组,各组平均粒径分别是54μm,73μm,97μm,145μm 和260μm。计算与试验对应进行6.5h,在10min (初始)和390min (结束)的结果和测量进行比较(如图5-17所示)。由于床沙粗化,泥沙浓度随时间过程衰减,相应床沙中径粗化后D50也和水槽试验一致。

图5-13 三维数学模型计算 (Zhou,1998)得到的断面流速和浓度分布与试验结果的比较
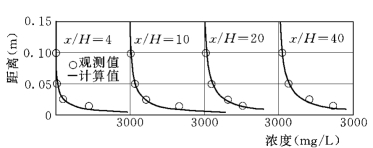
图5-14 用边界条件 (5-8)计算(Lin 和Falconer,1997)和DHL试验测量浓度比较
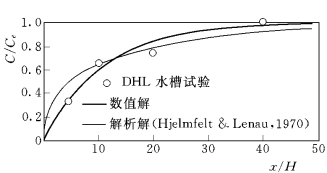
图5-15 方程 (5-33)计算与解析解 (Hjelmfelt et al,1970)及DHL试验平均泥沙浓度比较
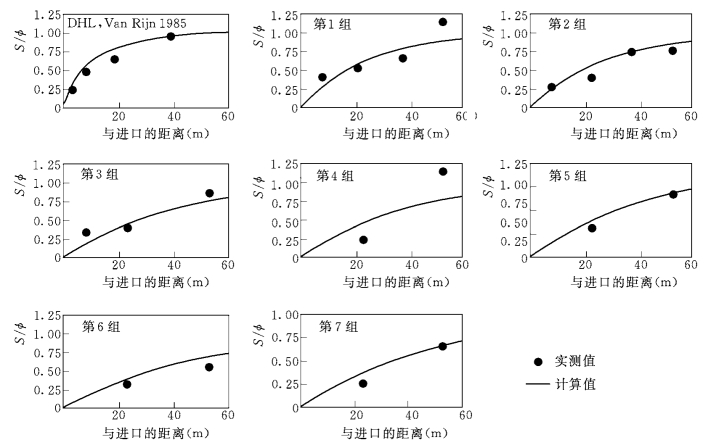
图5-16 方程式 (5-33)计算与大型水槽试验资料 (Van Rijn,1985)比较
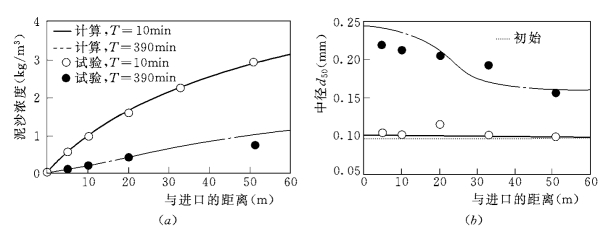
图5-17 一维模型计算结果和张启舜 (1962)不均匀沙清水冲刷试验结果比较
6.与王正兵等试验比较
Wang和Riberink(1986)在Delft技术大学进行了单向淤积试验 (如图5-3所示)。根据图5-3给出的不同位置断面浓度分布,可以计算出每个断面的平均浓度。由于试验在水槽底板上布设了带孔的集沙设施 (开孔率33%),泥沙一旦沉降到床面就不能再悬浮,所以,对用本试验的验证可进一步假设解式(5-33)中Φ=0:
![]()
可见,试验结果可直接检验淤积时恢复饱和系数的正确性。试验水槽长30m,泥沙在进口加入,前10m 为定床;中间长16m 段为带孔板有效试验段;后面4m 作为尾水稳定用。在中间段进口,采集泥沙浓度分布,作为上游边界条件。试验选基本均匀天然沙:D90=0.105mm,D10=0.075mm,D50=0.095mm。水力条件:H=0.215m,U=0.56m/s,水槽宽B=0.5m,根据Stokes公式计算沉速ω=0.00806m/s(水温20℃,也给出15℃水温结果),考虑床面层高度,计算水深0.21m。图5-18给出由式 (5-33′)计算的结果和试验平均浓度比较。可见,前段计算平均浓度和试验值接近,但计算浓度仍偏大,表明恢复饱和系数仍偏小。后段试验浓度偏大,由于试验沙不是绝对均匀的,沉降过程中泥沙是逐步分选的,后部悬沙粒径应该偏小,但这在计算中不能反映,后段试验值偏大是合理的。图中同时给出了恢复饱和系数α=0.25的情况,计算与试验是偏离的。
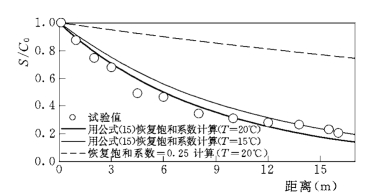
图5-18 单向淤积 (Wang 和Ribberink,1986)试验和计算相对平均浓度比较
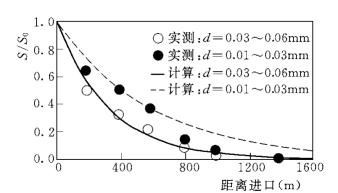
图5-19 不平衡输沙计算结果和王旺庄沉沙渠实测资料 (朱鹏程等,1964)比较
7.与王旺庄沉沙渠道资料比较
在不均匀沙淤积情况下,引黄灌区王旺庄沉沙渠道实测资料(朱鹏程等,1964)也可用于验证。实测沿程垂向泥沙浓度资料见图5-2。测量将泥沙分成0.01~0.03mm 和0.03~0.06mm 两组。计算采用同样分组,相应组平均粒径取为0.015mm 和0.045mm,沉沙渠水力条件:U=0.4m/s,J=0.2‰,H=0.31m,U*=0.0248m/s。由于是单向淤积情况,所以对每组都采用均匀沙计算。验证仍针对解析式 (5-33),检验恢复饱和系数。图5-19显示,实测和计算泥沙相对浓度吻合都良好,其中细组泥沙在沉沙渠后部计算偏大,可能和渠道中细沙在流速和紊动减小出现絮凝有关。对此没有资料证明。
有关泥沙研究进展的文章

实验室如果不能充分利用能力验证所给出的相关信息,而仅关注其结果的满意与否,那么实验室参加能力验证的价值将非常有限。能力验证结果的利用,会涉及实验室所有层级的人员,从一般技术人员到最高管理层。质量管理人员应参与能力验证结果的利用,尤其是对连续能力验证计划结果的利用。最高管理层不一定要熟悉能力验证的具体运作,但要正确理解能力验证的作用,以避免错误的利用能力验证结果。......
2023-06-29

表9-2评估参数的值在下文中,评估中使用的性能指标是平均节能。从图9-16可以看出,当网络负载低于50 Mbit时,MH-DBA的平均节能率为0.85,而3M-DBA的平均节能率为0.28。当网络负载超过300 Mbit时,控制器节能率开始趋于平稳。图9-17丢包率与平均节能率当吞吐量趋于稳定时,我们总结出能量效率的结果。随着网络负载的增加,两种机制的节能率降低,这是因为系统触发睡眠机制的概率会随着负载的增加而降低。......
2023-06-19

对于F-RoFN的CSRP控制层,OC服务器被分配来支持所提议的架构,并通过3种虚拟机进行CSP控制、网络虚拟化和PCE方案。控制器和OFP传播时间的方案处理时间分别为1 ms和0.5 ms。然而,很明显在1∶1保护的情况下,网络传输成功率下降缓慢。总之,该机制能够准确地提高网络的安全性。最下面的几何图形表示网络没有保护,而其余的几何图形图形代表网络,分别为1∶1、2∶1和3∶1保护的网络。......
2023-06-19

不过,要发挥表扬对幼儿的作用,不妨采用以下方法和技巧。在表扬幼儿时,如果将多种表扬方式综合在一起,更能发挥激励幼儿的作用。信的内容都是佳佳每天在幼儿园取得进步的表扬。因此,教师要科学地表扬幼儿,要注意通过观察和了解幼儿,再选择恰当的表扬方式适度表扬,对幼儿给予帮助,能更好地激发幼儿自我成长。这种表扬,就是对幼儿某种行为的结果进行反馈和评价,强调其成绩。......
2023-07-04

在最根本的层面上,社会事实只有三个大类:观念、行动和结果。这三类客体在本体论上是不同的,尽管它们以分层的方式相互关联,同时行动和结果都有不止一个尺度。选民实际给克林顿投了票,这是一个行动。而克林顿赢得选举的事实则是一个结果。当实证社会科学家对观念感兴趣时,他们主要感兴趣的是行动和社会结果的直接或间接的观念动力。......
2023-08-16

电流密度J的分布情况通过求解公式(6-1)来获得。在本节中,动静导电杆的材料采用铜,动静触头的材料采用银,电弧的电导率为银的10-4。在ANSYS有限元软件中进行静态传导电流分析,需要经过单元类型选择、定义材质属性、分配材质属性、几何模型剖分、定义边界条件、加载激励和结果处理这几个步骤。将上一步所得电流密度分布情况作为激励加载至模型上,通过有限元分析计算,可以得到灭弧室内的空间磁场分布。......
2023-06-15

设计本章的迁移学习模型。将特征提取模块和分类器模块级联,即为本章设计的迁移学习模型。设置模型训练的超参数值。在初步训练分类器模块时,设置学习率为0.001,初步训练的轮数设为两轮。对整个模型进行微调训练。......
2023-06-29
相关推荐