长江中下游河道在自然条件下长期不断的调整，河道总体冲淤达到相对平衡，反映在基本河槽年际冲淤交替，没有出现抬升或下切的趋势。荆江和洞庭湖关系的调整引起城陵矶至武汉河段发生较大幅度的冲淤变化。综上所述，江湖关系的调整导致下荆江下泄水沙量相对加大，而洞庭湖入汇的水沙量虽相对减小，含沙量却持续减小，因此城陵矶以下河道曾一度发生淤积，但1985年以后螺山站含沙量无增大趋势，该河段亦无继续淤积抬高趋势。......
2023-06-23
天然河道一维数学模型计算冲淤的断面修正方法
【摘要】：对一个典型得 “U”形河槽，图5-7给出了冲刷和淤积时分配系数BδZb/δAs沿断面的分布情况，表明理论结果反映了泥沙冲淤在滩槽的定量分配规律。
同前面分析，考虑一个微分流管，在此流管上冲淤可直接根据流管的河床变形方程计算
沿断面侧向积分方程式(5-29)，而且再次应用式(5-24)可得
将式(5-29)、式(5-30)写成差分，利用式(5-26)等可得垂线冲淤厚度与断面冲淤面积关系
式中:δZb为河道横断面上各垂线的冲淤厚度;δAs为一维计算给出的断面冲淤面积。
因为α=f(R)=f(Rc/η0.5)，Rc=6ω/κU*是断面平均悬浮参数，由式(5-31)结合图5-5可以看出:在淤积情况下，α沿河宽方向变化较小，而且水深较小的地方R 大，α偏大，淤积是按小于指数(3v-1)m 的关系沿不同水深分布的，相对比较均匀。相反，在冲刷情况下，α沿河宽方向变化很大，水深较大处R 小、α 远大于水深较小的地方，冲刷是按远大于指数(3v-1)m 的关系沿不同水深分布的，冲刷主要集中于深槽。这一结果与河流泥沙冲淤的普遍规律“淤积一大片，冲刷一条线”是吻合的。对一个典型得 “U”形河槽，图5-7给出了冲刷和淤积时分配系数BδZb/δAs沿断面的分布情况，表明理论结果反映了泥沙冲淤在滩槽的定量分配规律。
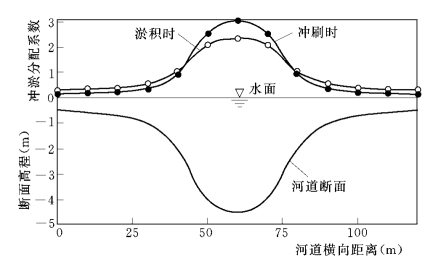
图5-7 典型的 “U”形河槽冲淤在滩槽分配的比例
有关泥沙研究进展的文章
- 详细阅读
-
天然河道一维恢复饱和系数的研究详细阅读
所以，不能直接应用于天然河道一维泥沙计算，为此，本节采取侧向积分法推导适于天然河道总流的不平衡输沙方程即恢复饱和系数。可见，天然河道恢复饱和系数小于矩形渠道数值。而且，随河道水位变化，恢复饱和系数在平滩水位附近存在一个最小值。根据河流动力学研究，河道平滩水位的造床作用最大，因此，利用天然河道冲淤资料反算或率定恢复饱和系数可能突出反映了造床流量的效果，得到的恢复饱和系数较小。......
2023-06-22
-
泥沙冲淤对环境的影响分析详细阅读
图8.2-1三峡水库各研究方案不同区间下泄流量年平均出现天数泥沙冲淤影响计算采用第5章一维非恒定流不平衡输沙水流泥沙数学模型研究成果。表8.2-5三峡水库泥沙冲淤计算方案8.2.3.1 水库泥沙淤积影响不同汛限水位方案运用50年，水库淤积量计算结果见表8.2-6和图8.2-2。......
2023-06-21
-
坝区河段泥沙冲淤变化及河势演变情况详细阅读
如葛洲坝水利枢纽运用后，坝区上游河段1981年4月～1991年11月共淤积1560万m3，此后变化不大，其中南津关峡谷段总体为淤积，但年际间仍有冲淤交替变化。......
2023-06-23
-
修正模型冲沙时间考虑非恒定流过程详细阅读
在非恒定流阶段的最后10min内，形成了较大的水面比降，水流达到了充足冲刷能力，必须按悬移质泥沙冲淤时间比尺计算这个时段的原型历时，结果为225min。因此模型中有充足冲刷能力的非恒定流时段不会超过整个冲沙时间的1/6。图4-23根据实测非恒定流过程分解模型冲沙历时示意图由图4-23可见，沿程水位变化过程中和稳定后，开闸泄水形成的水面比降集中在隔流堤头至其下游700m 左右的范围内。......
2023-06-22
-
冲裁模刃口尺寸计算方法及注意事项详细阅读
冲裁凸、凹模的刃口尺寸和公差直接影响冲裁件的尺寸精度。2）由于冲裁中凸模、凹模的磨损，故在设计落料时，凹模公称尺寸应取制件尺寸公差范围内的较小尺寸；设计冲孔时，凸模公称尺寸应取制件尺寸公差范围内的较大尺寸。冲孔部分以凸模为基准，且凸模磨损后该处尺寸减小。......
2023-06-26
-
河道汇流计算与水文分析详细阅读
河道汇流计算就是利用河段中的蓄泄关系与水量平衡原理把上断面流量过程演算成下断面流量过程，常用河槽汇流曲线进行演算。此汇流曲线用于河道洪水演算的优越性，在于它能考虑演算河段中区间汇入的各支流各自的入流点距下游断面的远近而应受到的不同大小的调节作用。2）华水汇流曲线。......
2023-08-23
-
探讨泥沙冲淤对社会和自然生态的重要性分析详细阅读
表8.3-6三峡水库运用50年时不同提前蓄水方案计算干流有效库容损失8.3.3.2 出库泥沙影响表8.3-7为三峡水库运用不同时期各提前蓄水方案的出库沙量。此外，由8.2.3节可知，目前三峡水库出库泥沙在长江中下游河道输沙中已基本属于冲泻质，三峡水库出库泥沙减少将直接减少沿程相应输沙量，但对沿程河道冲刷影响不大。......
2023-06-21
相关推荐