三维泥沙运动的河床边界条件优化

2025-09-29 理论教育版权反馈

【摘要】：在求解上述方程或根据其积分推求平面二维和一维不平衡输沙方程都需要给定河床表面的边界条件。目前，关于河床边界条件的提法很不统一。第三类边界条件不是正确的选择，合理的边界条件只有在第一或第二类中选取。在这样条件下，床面泥沙浓度不是独立变量，不能作为边界条件。

在三维条件下，不恒定悬移质泥沙运动的基本方程是(钱宁等，1983):

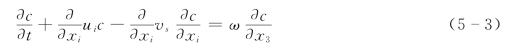
pagenumber_ebook=190,pagenumber_book=174

式中:c为泥沙浓度;xi为三维空间坐标;ui为流速矢量;vs为扩散系数;ω 为沉降速度;t为时间。

在求解上述方程或根据其积分推求平面二维和一维不平衡输沙方程都需要给定河床表面的边界条件。目前，关于河床边界条件的提法很不统一。系统归结起来有Dirichlet、Neumann和混合三类边界条件，这三类条件分别可以表述为

第一类

第二类

第三类

式中:zb为河床表面高程;a 为床面层厚度;ca为平衡条件下河床临底泥沙浓度;φ0为与泥沙浓度过程c无关的已知函数。

关于上述边界条件选择，注意到恒定和接近平衡时，式(5-3)具有简便形式

pagenumber_ebook=190,pagenumber_book=174

可见:

(1)在φ0=0时，条件式(5-6)与式(5-7)的形式完全一致，在没有第一类或第二类边界条件配合情况下，第三类边界条件不可能独立用于求解方程式(5-7)。

(2)在一般条件下(φ0≠0)，条件式(5-6)和方程式(5-3)在河床表面附近是矛盾的。

(3)退一步，或许可认为条件式(5-6)中的c和∂∂xc3的线性组合系数不一定是ω 和vs，而是任意的其他常数，使条件式(5-6)和方程式(5-3)满足独立，根据线性代数理论，这时在河床表面附近可以完全同时确定c和∂c/∂x3，即式(5-4)和式(5-5)两个条件同时成立，这为式(5-3)带来累赘边界条件，在理论上是不正确的。

考虑到接近恒定和平衡的状态是泥沙运动过程中非常重要的状态之一，由上述分析可见第三类边界条件或更任意组合的混合边界条件和基本方程式 (5-3)也是相关或矛盾的。第三类边界条件不是正确的选择，合理的边界条件只有在第一或第二类中选取。

对平衡情况，条件式(5-4)和式(5-5)完全等价。但是，对于不平衡输沙条件，两类条件有根本差别。对于超饱和的淤积过程，床面附近的泥沙浓度应该与其上部水体中的泥沙浓度有关，水体中的泥沙浓度决定于上游来沙条件。所以，不存在与水流条件呈单一关系的底部浓度条件。在这样条件下，床面泥沙浓度不是独立变量，不能作为边界条件。而在这时，实验室和野外资料都显示床面附近的泥沙浓度梯度具有很好的独立性，似可作为边界条件的选择;另一方面，对于次饱和冲刷过程，水流冲刷使泥沙向饱和状态发展的实质是底部冲刷使泥沙浓度从河底向水体上部不断扩散的过程，浓度梯度的调整是实现扩散的重要环节。根据大量的试验资料，在清水冲刷过程中，底部浓度趋于饱和可以远快于平均浓度的趋于饱和的过程。浓度的恢复实际上是沿程的垂向浓度分布剖面函数不断从“瘦”变“胖”的过程。这时底部浓度梯度是不断变化的，不存在与水流条件成单一关系的浓度梯度，即底部浓度梯度不是独立变量。而试验资料显示，这时浓度相对变化不大，相比之下底部浓度作为边界条件似更合适。(https://www.chuimin.cn)

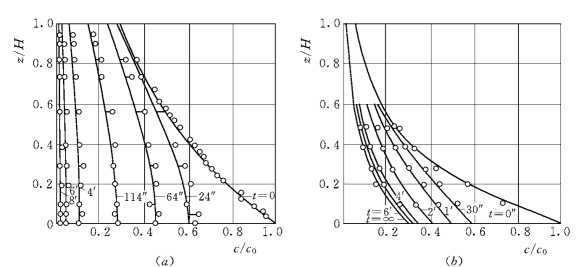
pagenumber_ebook=191,pagenumber_book=175

图5-1　Dobins(1943)转筒实验资料证明淤积过程中床面浓度梯度边界条件的合理性

(a)旋转格栅停止转动;(b)旋转格栅转动速度减慢

上述论证，可以通过试验或原型资料加以证明。对于淤积情况，图5-1是Dobins(1943)的转筒悬浮泥沙试验的资料。试验中初始泥沙浓度分布是由格栅搅拌产生。平衡后，转动格栅减速或完全停止，让筒内泥沙淤积和建立新的浓度分布。过程中实测浓度分布的变化如图所示。在泥沙浓度减小过程中，底部泥沙浓度不断减小，而其梯度却很快调整到最终状况而且长期保持给定值。可见，对于这样的超饱和淤积试验情况，给定底部浓度是不正确的，而给定底部浓度梯度似具有一定的可能性。比如，对于搅拌格栅完全停止的工况[图5-1 (a)]，假设底部梯度为零是非常合适的。

pagenumber_ebook=191,pagenumber_book=175

图5-2　沉沙渠道实测资料显示，淤积时床面泥沙浓度梯度保持常数，而浓度不断变化朱鹏程等 (1964)

(图例中的数据是距离渠道进口的长度)

淤积情况的第二个资料是在黄河灌区王旺庄沉沙渠道的资料 (图5-2，朱鹏程等，1964)。渠道水流速度基本上是恒定的，具有一定的挟沙能力，只有粗沙沉降，而大约50%的细沙可以输送。浓度变化过程中，床沙面泥沙浓度不断减小，但是，床面附近的泥沙浓度梯度始终保持给定数值。可见，渠道淤积条件下的底部浓度和梯度变化过程与Dobins的试验具有一致性。

淤积情况的第三组资料是Delft技术大学水槽试验 (Wang and Ribberink，1986)。试验是用底部带孔板的水槽模拟单向淤积过程 (如图5-3所示)。由于床面限制再悬浮发生，所以，除进口断面外，测量得到的底部泥沙浓度梯度沿程几乎是接近于0。

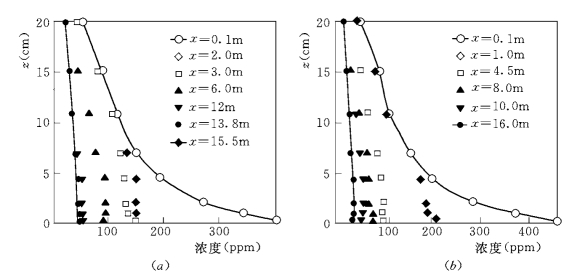
pagenumber_ebook=192,pagenumber_book=176

图5-3　淤积水槽试验揭示底部浓度梯度沿程按常数变化(Wang 和Ribberink，1986)

可见，模拟淤积情况时底部泥沙浓度不能作为边界条件，只有浓度梯度是相对合适的选择。

对冲刷情况，图5-4 (a)是Van Rijn(1985)的30m 水槽试验资料。试验完全模拟清水冲刷情况，进口没有泥沙，水流中的泥沙完全由河床冲刷形成。在图5-4 (a)中，底部附近(z=0.015m)的实测泥沙浓度是相对稳定保持不变。第二组资料可引用张启舜(1962)的试验成果。图5-4 (b)的资料显示，在清水冲刷的情况下尽管泥沙浓度沿程恢复和变化很大，但是所有断面实测的浓度分布剖面都从大约10kg/m3的浓度开始。可见，如果模拟冲刷的情况，选取底部浓度作为边界条件是合理的;而浓度梯度与过程有关，不能作为独立边界条件。

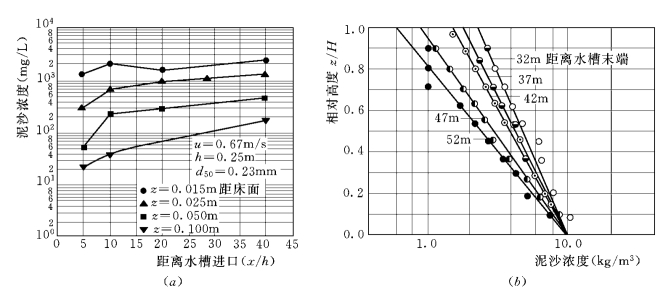
pagenumber_ebook=193,pagenumber_book=177

图5-4　冲刷试验测量的床面附近的泥沙浓度基本保持不变

(a)Van Rijn(1985)的试验;(b)张启舜 (1962)的试验

综合上述分析，对实际的不平衡泥沙运动，冲刷和淤积可能在同一个时空内同时发生，为了综合反映这一实际问题，最好的选择就是将上述条件组合起来考虑。即

pagenumber_ebook=193,pagenumber_book=177

三维泥沙运动的河床边界条件优化

相关推荐