可是,事实上,却很少在国内发现有推广设计CAE的优秀事例。不从认识上消除这些担心,就难以在设计现场推广应用CAE,这也是没有引进设计CAE的一个原因。现在本田大量地采用了设计CAE,实现了从KKD设计到设计CAE的转变。在领导人员认识和理解了设计CAE的重要性和优越性以后,问题就成功了一半。特别要注意采用那些设计人员易于熟悉的工具,如与CAD系统集成的CAE工具。......
2025-09-29
将前文的颗粒相模型应用到二维明渠恒定均匀流,考察模型在明渠水流中的适用性。选择颗粒相参数条件变化较大的Einstein和Chien (1955)、Wang和Qian (1989)的水槽试验资料进行分析。试验都使用了天然沙,颗粒粒径分别为1.3mm、0.94mm、0.274mm 和0.15mm,0.1H (H 为水深)处的体积比浓度C0.1为0.14%~9.10% (含沙量3.71~241kg/m3)。表3-3给出0.1H 处体积比浓度大于1.0%的试验组次的流动条件。其中,Re=udp/νf为沙粒雷诺数,u为剪切流速。
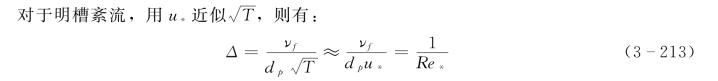
各组次下的Δ 和C0.1/Δ 也列于表3-3。由表可见,在0.1H 处,各个组次的C0.1/Δ 都大于0.1,并有5个组次的C0.1/Δ 大于1。因此,在该水深处,颗粒的碰撞效应不可以忽略;并且,相近的流动条件下,粗颗粒的C0.1/Δ 要显著大于细颗粒的相应值,粗颗粒的碰撞效应更加明显。
表3-3 Einstein和Chien(1955)和Wang和Qian(1989)部分试验组次的流动条件
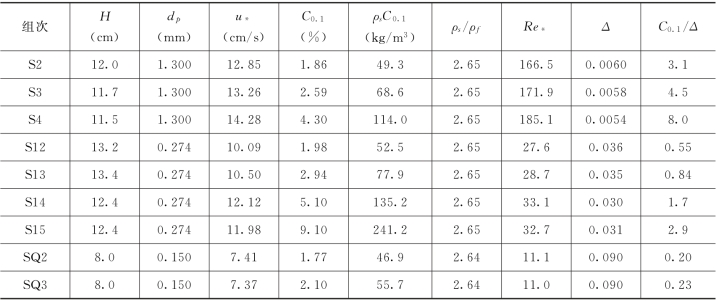
为了模拟上述明槽水流中的泥沙运动规律,应用前文的颗粒相动量方程式(3-143)、能量方程式(3-144)和本构关系式(3-159)、式(3-160),液相紊动与颗粒作用关系采用式(3-173)和式(3-174)。考虑到表3-3中各组次的C0.1不超过10%,为计算方便,忽略动量方程和能量方程中的碰撞应力、脉动能碰撞传导通量。那么,动量方程和能量方程分别简化为式(3-190)和式(3-191)。本构关系中的各参数也简化为:
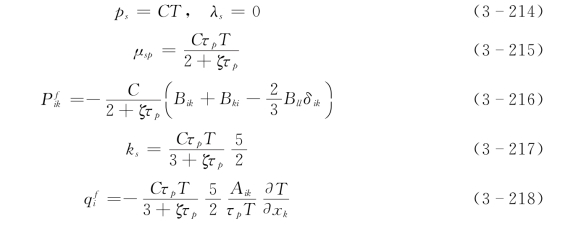
由式(3-215)~式 (3-218)可见,虽然忽略了颗粒相碰撞应力和脉动能碰撞传导通量,简化后的本构关系仍然部分考虑了碰撞效应,因而与完全忽略碰撞效应的式 (3-193)~式(3-196)形式不同。
在二维明槽恒定均匀流下,设x 表示水流方向,y 表示垂直方向,考虑作用于颗粒上的重力、浮力、升力等外力,忽略泥沙颗粒的布朗运动,颗粒相的动量方程和脉动能方程将简化为(傅旭东和王光谦,2003a;Fu et al.,2005):
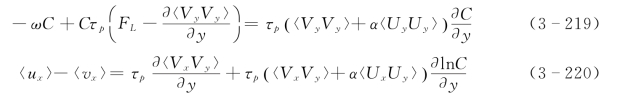
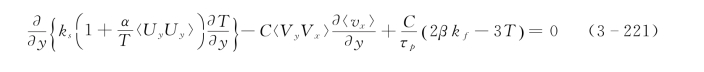
式中
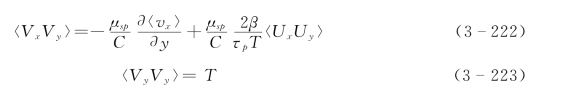
考虑到泥沙颗粒的离散特征,在床面附近采用碰撞—滑移边界条件 (Jenkins,1992;Louge et al.,1991;Cao和Ahmadi,1995;Fu et al.,2005):
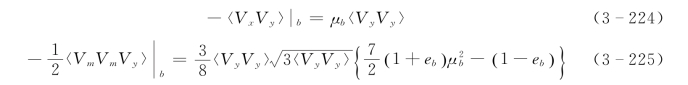
式中:下标b表示床面,eb=0.7为床面碰撞恢复系数;μb=0.23为床面滑动摩擦系数。在水流表面, 〈vx〉和T 采用零梯度边界,浓度边界采用底部实测值。

图3-18 水沙两相混合物平均速度的计算与试验资料比(https://www.chuimin.cn)
对液相水流的平均流速分布用对数尾流率来描述,紊动特性采用Nezu 和Rodi(1986)的经验公式。图3-18为计算的固液两相质量加权平均速度与试验资料的对比,其中,um为加权平均速度。可见,采用对数尾流率和方程式(3-220)可以很好地模拟计算试验中的混合物平均速度。
图3-19~图3-21给出了粗颗粒(dp=1.3mm)、细颗粒(dp=0.15,0.274mm)浓度分布的计算与试验资料的对比。作为比较,还用传统泥沙扩散方程式(3-226)计算泥沙颗粒的浓度分布,该方程也是Rouse浓度分布公式的理论基础:
![]()
由图可见,对于细颗粒泥沙,方程式(3-219)和方程式(3-226)给出的模拟结果相差不大,都能合理地符合试验资料。对于粗颗粒泥沙,方程式(3-219)仍能很好地再现试验浓度分布,方程式(3-226)的模拟结果却有明显的误差。在计算中,两个方程都采用了近壁实测点作为浓度参考点。因此,该点以上的浓度预报差异主要是由于方程结构差异引起的。对比两个方程可见,传统扩散方程式(3-226)仅描述了泥沙运动的重力沉降和水流紊动扩散机制,方程式(3-219)除了描述这两个机制外,还包含了升力、泥沙颗粒的应力梯度的影响,并反映了颗粒的漂移扩散机制(Fu et al.,2005)。
图3-22和图3-23分别给出了方程式(3-219)中的泥沙扩散系数和漂移扩散系数的分布。其中,扩散系数εyy和漂移扩散系数εpd分别定义为:

图3-19 粗颗粒天然沙浓度分布的计算与试验资料比较
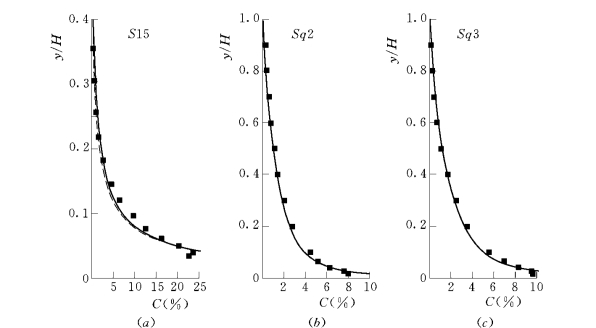
图3-20 细颗粒天然沙浓度分布的计算与试验资料比较 (符号说明同图3-19)
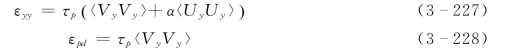
图中的无量纲扩散系数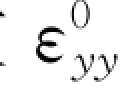 =εyy/uH,无量纲漂移扩散系数
=εyy/uH,无量纲漂移扩散系数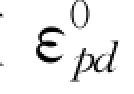 =εpd/uH。由图可见,随着颗粒浓度的增大,泥沙扩散系数减小,但漂移扩散系数增大。这是由于浓度较大时,水流运动受泥沙影响明显,导致水流紊动扩散系数的减小;同时,浓度的增加会导致颗粒之间作用的增强,相应地有漂移扩散系数的增大。从两图对比还可以看到,虽然粗颗粒的浓度低于细颗粒的浓度,但因为粗颗粒的惯性更大,相应地有粗颗粒的漂移扩散系数明显大于细颗粒的漂移扩散系数。在垂向上,在0.2H 以上,漂移扩散系数沿垂线向下增加。在0.1H 以下,细颗粒泥沙的漂移扩散系数向床面递减,呈现出与水流垂向紊动强度类似的分布特征;粗颗粒的漂移扩散系数却向床面快速递增。这也表明,细颗粒泥沙能够较好地响应水流紊动,因而具有与水流类似的紊动特性;粗颗粒泥沙由于较大的惯性、与床面频繁的碰撞交换等原因,因而与水流紊动迥然不同。
=εpd/uH。由图可见,随着颗粒浓度的增大,泥沙扩散系数减小,但漂移扩散系数增大。这是由于浓度较大时,水流运动受泥沙影响明显,导致水流紊动扩散系数的减小;同时,浓度的增加会导致颗粒之间作用的增强,相应地有漂移扩散系数的增大。从两图对比还可以看到,虽然粗颗粒的浓度低于细颗粒的浓度,但因为粗颗粒的惯性更大,相应地有粗颗粒的漂移扩散系数明显大于细颗粒的漂移扩散系数。在垂向上,在0.2H 以上,漂移扩散系数沿垂线向下增加。在0.1H 以下,细颗粒泥沙的漂移扩散系数向床面递减,呈现出与水流垂向紊动强度类似的分布特征;粗颗粒的漂移扩散系数却向床面快速递增。这也表明,细颗粒泥沙能够较好地响应水流紊动,因而具有与水流类似的紊动特性;粗颗粒泥沙由于较大的惯性、与床面频繁的碰撞交换等原因,因而与水流紊动迥然不同。
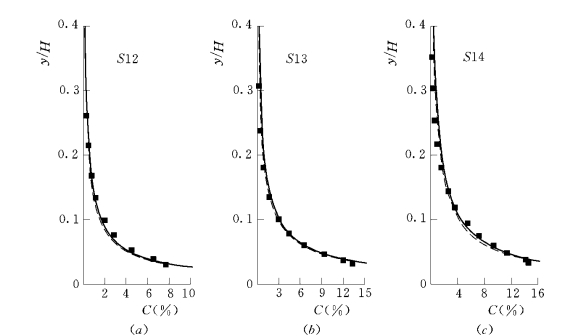
图3-21 细颗粒天然沙浓度分布的计算与试验资料比较 (符号说明同图3-19)
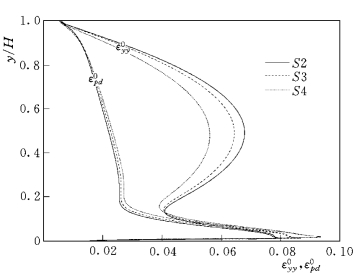
图3-22 粗颗粒的扩散系数与漂移扩散系数分布
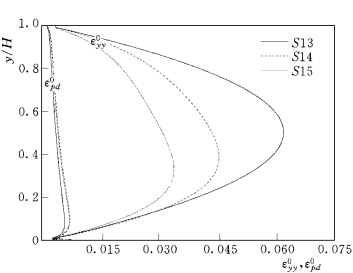
图3-23 粗颗粒的扩散系数与漂移扩散系数分布
(本章作者:傅旭东、王光谦,受国家自然科学基金委创新研究群体基金(50221903)和黄河联合研究基金(50309007)资助)
相关文章

可是,事实上,却很少在国内发现有推广设计CAE的优秀事例。不从认识上消除这些担心,就难以在设计现场推广应用CAE,这也是没有引进设计CAE的一个原因。现在本田大量地采用了设计CAE,实现了从KKD设计到设计CAE的转变。在领导人员认识和理解了设计CAE的重要性和优越性以后,问题就成功了一半。特别要注意采用那些设计人员易于熟悉的工具,如与CAD系统集成的CAE工具。......
2025-09-29

在梁的强度计算中,必须同时满足正应力和剪应力两个强度条件。通常先按正应力强度条件设计出截面尺寸,然后按剪应力强度条件进行校核。但在以下几种情况下,需校核梁的剪应力:①最大弯矩很小而最大剪力很大的梁;②焊接或铆接的组合截面梁;③木梁,因为木材在顺纹方向的剪切强度较低,所以木梁有可能沿中性层发生剪切破坏。按强度条件求许用荷载[F]。......
2025-09-29

同时良导体阻尼器也在磁路系统气隙中运动,感应产生涡流,形成系统的阻尼力,起衰减固有振动和扩展频率响应范围的作用。图2-45磁电式扭矩传感器工作原理图图2-45磁电式扭矩传感器工作原理图当被测转轴有扭矩作用时,轴的两端产生扭角,两个传感器输出一定附加相位差的感应电压U1和U2,这个相位差与扭角成正比。这样,传感器就把扭矩引起的扭转角转换成相应变化的电信号。......
2025-09-29

则B正比于Ui,霍尔器件的Uo正比于B。此角位移测量仪可以改造为霍尔电压传感器,测量直流电压。图3-14所示为霍尔传感器测量转速方法的示意图。在铁心上开一与霍尔传感器厚度相等的气隙,将霍尔线性器件紧紧地夹在气隙中央。......
2025-09-29

图3-4脉动应力与碰撞应力之比随浓度的变化上述颗粒流模型所描述的运动物理图景是颗粒碰撞作用为主、水流影响可以忽略不计的流动过程。无粘泥石流运动中,颗粒浓度非常高,泥沙颗粒的运动以碰撞作用为主,除了颗粒快速的空间位置交换和碰撞所产生的脉动应力和碰撞应力以外,还有颗粒之间相互挤压、摩擦产生的摩擦应力。颗粒相的总应力为:式中:Pij为总应力;为摩擦应力分量。......
2025-09-29

采用均相流模型中的质量输运空化模型,形式[141]如下:式中,分别表示质量蒸发速率和质量凝结速率;αν为空泡体积分数;ρν为汽体密度,其值为0.554 kg/m3。质量输运空化模型的质量蒸发速率和质量凝结速率,大多数为在Rayleigh-Plesset方程的基础上推导出来的,其形式为:式中,Rb为空泡平均半径,其值为10-6 m;ρl为液体密度,其值为997 kg/m3;pν为饱和蒸汽压力,其值为3 574 Pa;S为液体的表面张力;μ为液体的动力黏性系数。......
2025-09-29

工程中光滑铰链约束应用广泛,形式多样,常见的主要有以下三种类型:固定铰链支座约束、可动铰链支座约束、中间铰链约束。约束反力的作用线不能预先定出,但约束反力垂直于轴线并通过铰链中心。实例:在桥梁、屋架等结构中经常采用可动铰链支座约束,如图2-22 所示。若相连接的两个构件均不固定,则称为中间铰链。......
2025-09-29

图17.3.1 零件模型及模型树Step1.新建模型文件。选择下拉菜单命令,系统弹出“创建草图”对话框;选取XY基准平面为草图平面,单击按钮,进入草图环境,绘制图17.3.2所示的草图1;单击按钮,退出草图环境。在绘图区选取YZ基准平面为草图平面,添加图17.3.3所示的草图2。选择图17.3.10a所示的边链为边倒圆参照,并在文本框中输入值2,完成边倒圆特征2的添加。Step8.添加图17.3.10b所示的边倒圆特征2。......
2025-09-29
相关推荐