简单剪切流模型的有效性验证

2023-06-22 理论教育版权反馈

【摘要】：这些试验中的浓度和剪切率等参数都在较大范围内变化，可以验证前述颗粒相模型的预测性能。表3-2中列出了详细的试验条件。

为了验证上述基于颗粒运动Lagrange方程的颗粒相模型，考虑高浓度的水沙混合物的简单剪切流动(Wang et al.，2005)。该流动中，不存在泥沙颗粒浓度和脉动能的空间梯度。

3.4.5.1　水沙两相的无量纲能量方程

令x 和y分别表示沿流向和侧向的坐标，在没有体积力、压力梯度力和恒定流条件下，水流和颗粒相的平均速度满足(Ma和Ahmadi，1990):

式中:U 为空间一点的平均流速。

由于没有对流和扩散，水流和泥沙颗粒的能量方程为 (Ma和Ahmadi，1990;Zhang和Reese，2001):

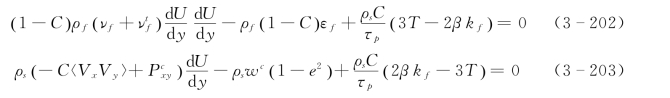
pagenumber_ebook=146,pagenumber_book=130

式中:kf和εf分别为水流紊动能和紊动能耗散率; pagenumber_ebook=146,pagenumber_book=130 为水流的涡粘性系数。

水流紊动涡粘性系数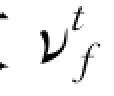 pagenumber_ebook=146,pagenumber_book=130 和紊动能耗散率εf分别如下:

pagenumber_ebook=146,pagenumber_book=130

式中:Cu=0.09为模型参数;lf为水流紊动耗散长度尺度。

根据Ma和Ahmadi(1990)的建议，lf与颗粒体积比浓度C 和流场特征长度尺度L等有关，在考虑颗粒浓度对水流紊动的影响后，有lf的表达式:

式中:Cm为颗粒最大体积比浓度，Cm=0.64。

选择Zaichik et al. (1997)关于Bik的表达式(3-174)，由式(3-159)及水流紊动切应力的涡粘性假设，有泥沙颗粒相正应力和切应力:

pagenumber_ebook=146,pagenumber_book=130

上述方程中的水流紊动—颗粒作用系数β选择形式简单的式 (3-172)。由于水流紊动参量的假设具有一定的近似性，与这种假设水平一致，还假定沿颗粒轨道的水流紊动拉格朗日积分时间尺度TLp等于水流质点的拉格朗日积分时间尺度TL:

为与Ma和Ahmadi(1990)一致，颗粒径向分布函数g0选择为:

pagenumber_ebook=147,pagenumber_book=131

为便于分析，将能量方程式(3-202)和式(3-203)无量纲化:

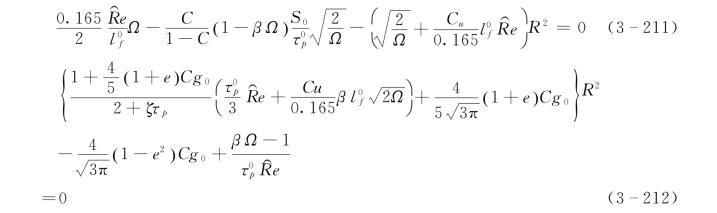
pagenumber_ebook=147,pagenumber_book=131

式中:各无量纲参数分别定义为:

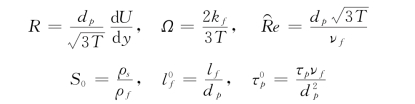
pagenumber_ebook=147,pagenumber_book=131

当无量纲方程中的固液两相密度比S0、碰撞恢复系数e、颗粒粒径dp、流场特征长度尺度L 和无量纲剪切率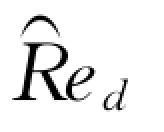 pagenumber_ebook=147,pagenumber_book=131 、颗粒体积比浓度C 确定以后，方程式(3-211)和式 (3-212)就成为参数R 和Ω 的非线性代数方程组。求解出R 和Ω 后，由式 (3-207)和式(3-208)就可以计算颗粒相正应力和切应力，也可以计算出相应的水流紊动正应力2(1-C)ρfkf/3和切应力(1-C)ρf(νf+ 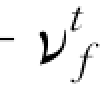pagenumber_ebook=147,pagenumber_book=131 )d U/d y，水沙混合物的总应力为颗粒相应力和水流应力的叠加。

3.4.5.2　与Bagnold (1954)、 Savage和Mc Keown (1983) 试验资料的验证对比

Bagnold (1954)和Savage和Mc Keown (1983)开展了系列的固液两相流的圆筒剪切试验研究。Bagnold (1954)探讨了蜂蜡圆球颗粒和水的混合物的应力行为，Savage和Mc Keown (1983)研究的是聚苯乙烯颗粒和盐水混合物的运动特征。这些试验中的浓度和剪切率等参数都在较大范围内变化，可以验证前述颗粒相模型的预测性能。

表3-2中列出了详细的试验条件。计算中所用的碰撞恢复系数e的取值与Ma和Ahmadi(1990)相同，e值和水流运动粘性系数νf的取值都一同列在表3-2中。

表3-2　Bagnold(1954)和Savage和McKeown(1983)的试验条件

pagenumber_ebook=147,pagenumber_book=131

1.应力—浓度、应力—剪切率变化关系

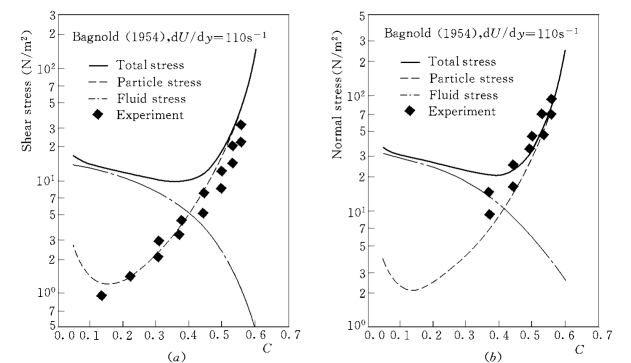
pagenumber_ebook=148,pagenumber_book=132

图3-10　计算的总应力、液相应力和颗粒相应力随浓度的变化及与Bagnold (1954)试验资料的比较 (粒径dp=1.32mm)

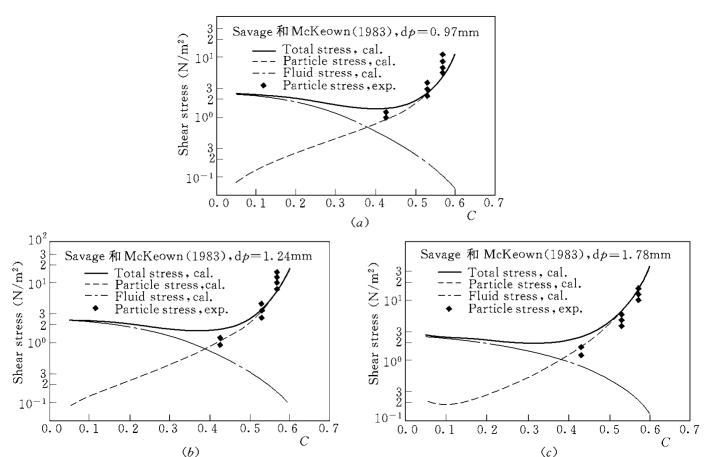
pagenumber_ebook=148,pagenumber_book=132

图3-11　计算的总应力、液相应力和颗粒相应力随浓度的变化及与Savage和Mc Keown(1983)试验资料的比较 (剪切率d U/d y=28s-1)

图3-10和图3-11分别给出了Bagnold (1954)、Savage和Mc Keown (1983)试验条件下，水沙混合物的总正应力和总切应力、泥沙颗粒相的正应力和切应力、水流的正应力和切应力随颗粒浓度的变化关系。其中，流场剪切率对Bagnold (1954)试验是110s-1，对Savage和Mc Keown (1983)试验是28s-1，都是试验中的典型剪切率。由图可见，除了在C＜0.15时与Bagnold (1954)资料有偏离以外，模型计算和试验测得的颗粒相应力无论在趋势上还是幅度上都符合很好。在C＜0.15时，模型计算出的颗粒相应力随浓度C 的减小而增加。这种应力随浓度减小而增加的趋势，Chen和Chang (1998)称之为“C→0 渐进行为”，在早期的快速颗粒流模型的验证中就已经发现 (Campbell，1990)。Chen和Chang (1998)认为快速颗粒流模型出现 “C→0渐进行为”是由于没有考虑隙间流体效应。

图3-10和图3-11还表明，随着颗粒浓度的变化，颗粒相应力在水沙混合物的总应力中所占比例也发生变化。在低浓度下，水流紊动应力在总应力中所占比例很高;在C＞0.5时，水流紊动应力可以忽略。比较之下，高浓度时的颗粒相应力是总应力中的主要组成部分;在C＜0.2时，颗粒相应力在总应力中可以忽略。这些浓度条件与Ma和Ahmadi(1990)的结论相一致。

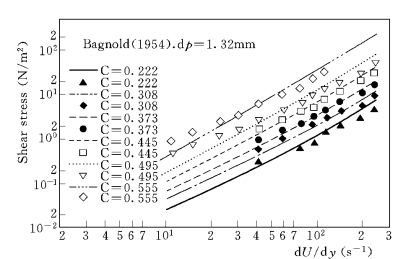
pagenumber_ebook=149,pagenumber_book=133

图3-12　计算的颗粒相切应力随剪切率的变化及与Bagnold (1954)资料的比较

图3-12和图3-13绘出了计算的颗粒相切应力随剪切率的变化曲线，并与试验资料进行了比较。在Bagnold(1954)试验条件下，虽然颗粒浓度和流场剪切率的变化范围较大，分别为0.22～0.56和10～240s-1，计算结果和试验资料都符合较好，只是在高颗粒浓度和低剪切率下略有偏差。在Savage和Mc Keown (1983)试验条件下，模型计算较为合理地给出了C=0.429 和0.53 时的试验结果;但在C=0.57时，计算结果显著低于试验值。出现这种偏差可能有三方面的原因:其一可能是试验装置的尺寸限制 (Ma和Ahmadi，1990)。这些试验中的剪切区域宽度仅为颗粒粒径的10倍，可能导致显著的边界效应，难以给出理想的水沙两相混合物的简单剪切流。其二可能是径向分布函数g0的影响(Chen和Ling，1998)。g0在高浓度时数值很大，不同的g0表达式下，相同的本构关系模型也会给出差异较大的应力。另外，在低剪切率和高浓度下，颗粒间的摩擦作用将变得重要，这在上述模型中没有考虑。

2.颗粒相切应力的水流效应

为了显示隙间水流对颗粒相切应力的影响，在不同剪切率下，基于颗粒相本构关系式(3-208)计算了切应力—浓度变化关系曲线，并绘于图3-14。作为对比，采用无水流紊动影响的本构关系式(3-183)、并假定ζτp≫1，计算了同样条件下的切应力—浓度变化关系曲线，绘于图3-15。图中的无量纲切应力是通过切应力除以ρs(dpd U/d y)2得到的。

由图3-14和图3-15可见，两种本构关系给出的颗粒相无量纲切应力曲线在低剪切率下具有显著差异。在d U/d y＜32.9s-1时，采用式(3-208)，不会给出C→0时的切应力随浓度减小而增加的现象。比较之下，采用式(3-183)，即使在d U/d y=2s-1时也给出了“C→0渐进行为”。由此可见，不考虑隙间水流影响，确实是快速颗粒流模型出现“C→0渐进行为”的一个原因。另外，在C＞0.2和d U/d y ≤50s-1时，式(3-183)给出的切应力低于式(3-208)的预报结果。这是由于式(3-208)中也含有水流紊动对颗粒相切应力的贡献。在剪切率高达d U/d y=200s-1时，两个本构关系式给出的切应力幅度和曲线形状近乎相同，这也说明高剪切率下的水流紊动影响可以忽略。

pagenumber_ebook=150,pagenumber_book=134

图3-13　计算的颗粒相切应力随剪切率的变化及与Savage和Mc Keown (1983)的比较

由图3-14还可看到，在流场剪切率从2变化到200s-1时，颗粒的运动模式也发生变化。在浓度较高 (如C＞0.2)时，随着d U/d y 的增加，无量纲切应力以递减的速率减小，这表明切应力逐渐变化到与剪切率的平方成正比。或者说，当d U/d y 足够高时，颗粒运动进入颗粒惯性模式 (Granular-inertia regime)。在该模式下，隙间水流不影响切应力—剪切率关系(切应力正比于剪切率的平方，图中的无量纲切应力不再随剪切率变化)。在d U/d y=200s-1时，两种本构关系的给出的切应力几乎相同也说明了这一点。式(3-183)虽然是快速颗粒流模型，但由于在求解耦合的能量方程式 (3-211)和式 (3-212)时，在一定程度上考虑了水流效应，该本构关系还是给出了类似的变化趋势，只是剪切率对切应力的影响较弱，如图3-15所示。

3.颗粒相应力的“C→0渐进行为”

式(3-208)的检验表明，在较高剪切率下会出项颗粒相应力的 “C→0 渐进行为”。在Bagnold (1954)试验条件下，图3-16给出了切应力—浓度关系曲线随剪切率的变化。由图可见，在d U/d y≤32.9s-1时，相同剪切率下的颗粒相切应力随着浓度的增加而单调增加。当剪切率超过32.9s-1时，对于每个剪切率，在切应力—浓度关系曲线上都存在一个临界浓度。该临界浓度下，颗粒相切应力最小;当浓度小于该临界浓度时，颗粒相切应力随着浓度的减小而增大，即出现“C→0 渐进行为”。

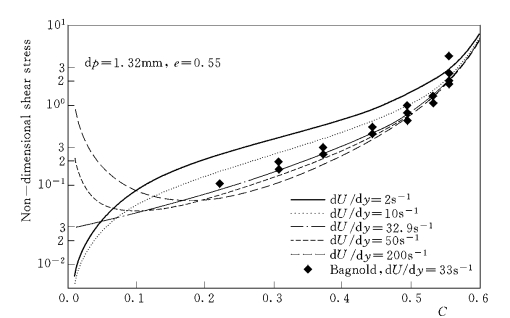
pagenumber_ebook=152,pagenumber_book=136

图3-14　剪切率对切应力一浓度关系的影响[Bagnold （1954）试验条件，两相流模型]

pagenumber_ebook=152,pagenumber_book=136

图3-15　剪切率对切应力—浓度关系的影响[Bagnold （1954）试验条件，快速颗粒流模型]

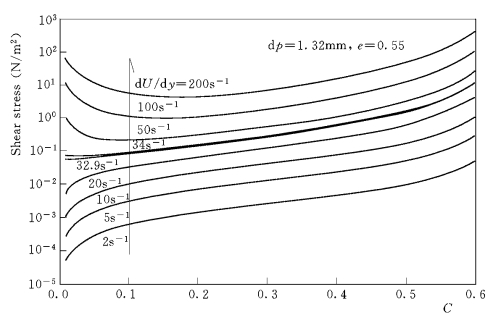
pagenumber_ebook=152,pagenumber_book=136

图3-16　剪切率对切应力—浓度关系的影响[Bagnold（1954）试验条件]

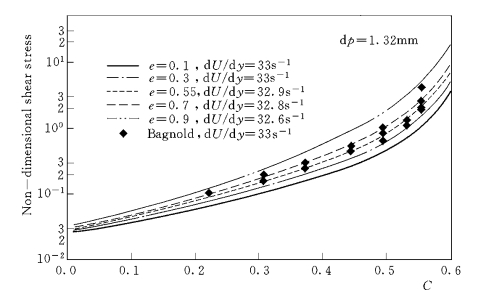
pagenumber_ebook=152,pagenumber_book=136

图3-17　碰撞恢复系数e对切应力—浓度关系的影响[Bagnold（1954）试验条件]

在能量方程式(3-203)中，颗粒相脉动能的剪切生成与碰撞耗散、相间传递平衡。随着颗粒浓度的减小，碰撞耗散以正比于C 2的速率减小，但能量剪切生成的减小速率与C 成正比。在高剪切率下，当颗粒浓度从较低值 (C→0)减小时，碰撞耗散和剪切生成的不同减小速率可能导致颗粒相脉动能的迅速增加，这反过来增大碰撞耗散率，使能量趋于恢复平衡。这是Bagnold (1954)试验条件下、d U/d y≥32.9s-1时的情形。在剪切率较小时(见图3-16中d U/d y ＜32.9s-1)，较低的能量剪切生成速率和相间能量传递，可能使得“C→0 渐进行为”不发生。

为考察不同碰撞耗散水平的影响，图3-17在不同碰撞恢复系数取值时，给出了临界剪切率下(流场剪切率超过该临界值时，“C→0 渐进行为”发生)颗粒相切应力—浓度关系曲线。由图可见，虽然碰撞恢复系数是颗粒的一种物理属性，不同的e值会显著地改变无量纲切应力的大小，但在Bagnold (1954)试验条件下，e值变化对临界剪切率几乎没有影响。在不同的碰撞耗散水平上 (e 从0.1 向0.9 变化)，该临界剪切速率几乎都在32.9s-1。这也说明，“C→0 渐进行为”可能是由于低浓度下的能量剪切生成与碰撞耗散的极度不平衡。

Chen和Ling (1998)将“C→0渐进行为”归因于快速颗粒流理论没有考虑隙间水流效应，前文不同形式的本构关系的结果对比也证实了他们的论述。显然，即使在极低剪切率 (如d U/d y=2s-1)下，快速颗粒流理论的能量方程中没有相间能量传递以及能量剪切生成与碰撞耗散的不平衡，流动中会出现 “C→0渐进行为”。但是，考虑了隙间水流效应的本构关系，在相对较高的剪切率下也会给出 “C→0渐进行为”，说明该渐进行为可能具有更为复杂的机理。如Campbell(1990)曾指出，该渐进行为也许对应着低浓度简单剪切流中的固有不稳定态。如果该渐进行为仅仅是理论模型的预报结果，在自然界中并不真实存在，那么可以推断，简单剪切流中还可能存在其他的能量耗散机制。这也说明，对能量耗散的精确模拟将有助于刻画水沙混合物简单剪切流动的稳定性。

简单剪切流模型的有效性验证

相关推荐