极限条件下的颗粒相模型优化

2025-09-29 理论教育版权反馈

【摘要】：若颗粒碰撞效应不占优势，相应的本构关系可以简化为:4.粒间碰撞可以忽略在一般条件下的本构关系中，参数ζτp反映了粒间碰撞对颗粒相应力和脉动能传导通量的影响。

上述本构模型考虑液相紊动和泥沙颗粒的相间作用、颗粒之间的碰撞作用，原则上可适用于不同浓度范围和颗粒惯性的水沙两相流。如前文关于快速颗粒流理论所分析的那样，由于水沙条件 (如浓度)的变化，流动性质和内部的力学机制可能会发生根本性变化，从而可以将流动分成不同的模式。如随着颗粒浓度的变化，颗粒相的碰撞应力和脉动应力的比值随之变化，流动可以分为稠密(高浓度)和稀疏 (低浓度)两相流。同样地，根据水沙相间作用的强弱程度的不同，可以区分颗粒相运动是水流紊动控制还是颗粒惯性控制。在惯性很大时，颗粒运动对水流紊动响应缓慢，可以认为水流仅对颗粒施加平均作用力，不用考虑水流紊动的影响。这与水流为层流的情形相类似。

1.水流为层流(〈UiUk〉=0)

水流为层流时，水流无紊动(颗粒运动会对水流产生扰动，但扰动的空间尺度很小)，〈fLUi〉为零，即Aik和Bik均为零。层移质运动、水石流、粘性泥石流等属于这种情形。此条件下，泥沙颗粒的动量方程和脉动能方程为:

相应的本构关系为:

式中:ps、λs、μsp和ks分别同式(3-161)、式(3-162)、式(3-163)和式(3-165)。比较上述动量方程、脉动能方程与快速颗粒流理论的对应方程式 (3-8)和方程式 (3-9)，可以看到方程的形式基本相同，都不存在水流紊动引起的泥沙扩散作用力，也没有了向水流输送的紊动能量。

2.颗粒惯性充分大(τp≫TLp)

如前文分析，该极限条件下，颗粒运动难以响应水流紊动，因而有Aik和Bik均趋于零。此条件下的泥沙颗粒动量方程、脉动能方程和对应的本构关系与水流为层流情形基本相同，如式(3-181)～式(3-184)所示。若脉动能方程式(3-182)中的布朗运动部分因颗粒惯性较大而可以忽略，相应的能量方程为:

2.颗粒惯性充分大(τp≫TLp)

3.颗粒惯性可以忽略(τp≪TLp)

如前文分析，该极限条件下，颗粒能够充分响应水流紊动，水流紊动对颗粒运动具有主导性影响。泥沙颗粒动量方程、脉动能方程为一般形式的方程式 (3-143)和式 (3-144)。若颗粒碰撞效应不占优势，相应的本构关系可以简化为:

3.颗粒惯性可以忽略(τp≪TLp)

4.粒间碰撞可以忽略(ζτp→0)

在一般条件下的本构关系中，参数ζτp反映了粒间碰撞对颗粒相应力和脉动能传导通量的影响。由τp和ζ 的定义式(3-133)、式(3-139)，不考虑水流紊动对碰撞频率的修正，有:(https://www.chuimin.cn)

4.粒间碰撞可以忽略(ζτp→0)

在一般条件下的本构关系中，参数ζτp反映了粒间碰撞对颗粒相应力和脉动能传导通量的影响。由τp和ζ 的定义式(3-133)、式(3-139)，不考虑水流紊动对碰撞频率的修正，有:

可见，参数ζτp不仅与颗粒粒径、浓度、脉动能等有关，还与固液两相的密度比有关。对于水沙两相流，由于ρs 与ρf量级相同，参数ζτp可以C dpT/νf估计。定义无量纲参数Δ:

则参数ζτp～C/Δ。在C≪Δ 时，ζτp→0，颗粒间的碰撞效应可以忽略。相应地，颗粒相动量方程和能量方程简化为:

本构关系也简化为与Zaichik et al. (1997)低浓度下的本构关系一致的形式:

5.颗粒碰撞占优势(ζτp→∞)

在C≫Δ 时，ζτp→∞，颗粒间的碰撞效应占优势。由式(3-188)可见，对于通常的水沙两相流，这需要在浓度较高或者颗粒较粗时才有可能实现;而对于气固两相流，由于气固两相密度相差悬殊，即使在较低浓度下，粒间碰撞也有可能处于主导地位。

5.颗粒碰撞占优势(ζτp→∞)

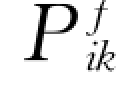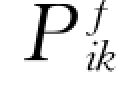该极限情形下，本构关系中的粘性系数μsp、脉动能传导系数ks、相间作用引起的应力 pagenumber_ebook=145,pagenumber_book=129 和相间作用引起的脉动能传导通量qif分别为:

上述本构关系与Ma和Ahmadi(1988)考虑隙间流体效应的本构关系相一致，不同之处在于这里还包括了相间作用引起的颗粒相应力和脉动能传导通量。

极限条件下的颗粒相模型优化

相关推荐