，k只用来标识特征序号，不表示特征的顺序。图7.3光流的（u，v）坐标和四方向、八方向划分示意图光流的（u，v）坐标和四方向示意图；光流的（u，v）坐标和八方向示意图图7.4从各行为视频中采集m1～m12散点图四方向运动速度。结果达到了目标，如图7.4所示，图中每个行为，利用了15长度的差分光流场序列，提取出15×12的特征数据，显示在一个散点图中。......
2025-09-29
颗粒流模型在工业中的应用
【摘要】：图3-4脉动应力与碰撞应力之比随浓度的变化上述颗粒流模型所描述的运动物理图景是颗粒碰撞作用为主、水流影响可以忽略不计的流动过程。无粘泥石流运动中，颗粒浓度非常高，泥沙颗粒的运动以碰撞作用为主，除了颗粒快速的空间位置交换和碰撞所产生的脉动应力和碰撞应力以外，还有颗粒之间相互挤压、摩擦产生的摩擦应力。颗粒相的总应力为:式中:Pij为总应力;为摩擦应力分量。
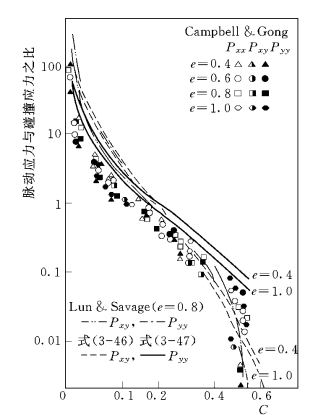
图3-4 脉动应力与碰撞应力之比随浓度的变化
上述颗粒流模型所描述的运动物理图景是颗粒碰撞作用为主、水流影响可以忽略不计的流动过程。在自然界中，层移质运动和水石流是这方面的典型例子。
无粘泥石流运动中，颗粒浓度非常高，泥沙颗粒的运动以碰撞作用为主，除了颗粒快速的空间位置交换和碰撞所产生的脉动应力和碰撞应力以外，还有颗粒之间相互挤压、摩擦产生的摩擦应力。颗粒相的总应力为:
式中:Pij为总应力;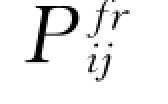
为摩擦应力分量。
考虑二维简单剪切流的情形，由于颗粒浓度高，脉动应力可以忽略，则式 (3-55)简化为:
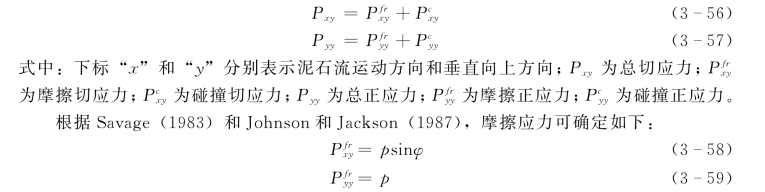
式中:p 为正应力;φ 为内摩擦角;均与颗粒浓度有关。
对于流深为H 的简单剪切流，由式 (3-42)、式 (3-43)和式 (3-58)、式 (3-59)，建立垂向y 点处沿流向和垂向的动量平衡关系:
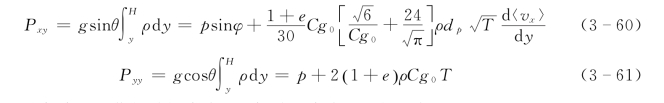
由上述动量平衡关系，获得总切应力Pxy与总正应力Pyy之比为
选择参考点y=ya，该点的颗粒相温度_为Ta，则有:
对于流动较快的泥石流，颗粒间摩擦作用很小。同时，若颗粒浓度很高，如C＞0.5，那么近似有如下条件成立:
这样，由式(3-62)有:(https://www.chuimin.cn)
在式(3-67)中，颗粒相温度是未知量，原则上由颗粒相的脉动能方程求解获得。就所讨论的流动情形而言，颗粒相温度一般符合图3-5所示，表示为函数形式 (王光谦等，1992):
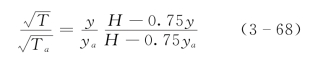
将式(3-68)代入式 (3-67)，对y 积分，假定平均速度在床面为零，有:
式中:vm为流动表面的最大流速。
用 Takahashi (1980)、 Wang (1990)、Tsubaki et al.(1982)、Savage(1979)等人的无粘泥石流 (或颗粒流)的流速实测资料验证式(3-69)，结果如图3-6～图3-9所示。可见，流速公式(3-69)的理论预测结果与试验资料符合的非常好。
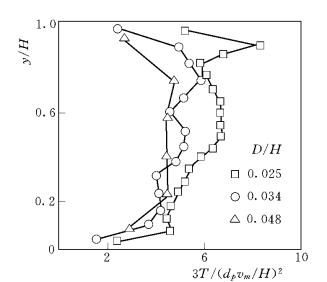
图3-5 无粘颗粒流温度的垂线分布
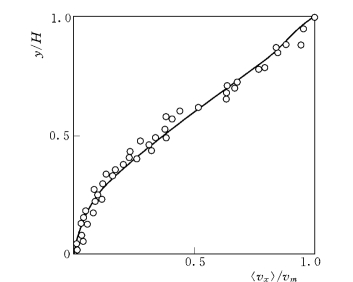
图3-6 流速分布计算与Wang (1990)试验资料的比较 (实线:计算;圆点:试验值)
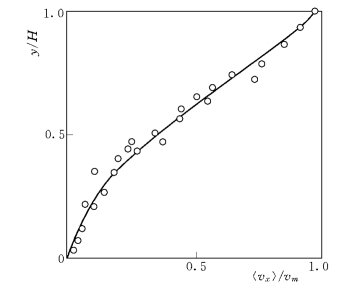
图3-7 流速分布计算与Takahashi(1980)试验资料的比较 (符号说明同图3-6)
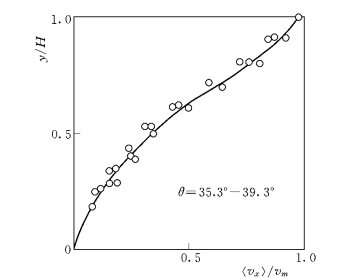
图3-8 流速分布计算与Savage(1979)试验资料的比较 (符号说明同图3-6)
图3-9 流速分布计算与Tsubaki et al. (1982)试验资料的比较 (符号说明同图3-6)
相关文章
- 详细阅读
-
创新设计方法论在工业设计中的应用详细阅读
机器外形和色彩的设计属于工业设计范畴。目前，工业设计是一个受到社会欢迎的热门行业，由于这一行业完成任务速度较快，且容易见到立竿见影的效果，而且很容易受到用户和市场的好评，以及加快对产品的销售。在工业设计中，可在产品的外形融入艺术方面的内容。工业设计的艺术性常常会影响商品在市场中的占有率。在工业设计中，要贯彻创新的思想，才能创造出过去没有的艺术成果，会给工业设计增加新的活力，并会产生积极的影响。......
2025-09-29
-
气体保护在镁工业中的应用及优化探讨详细阅读
SF6气体是目前镁工业中最广泛使用的保护气体。在进行镁熔炼保护时，通过将少量SF6气体和CO2气体及干燥空气充分混合以后覆盖在镁熔体表面进行保护。鉴于以上原因，SF6已经受到环境保护人员的严重关注。一些工厂及研究机构对SO2的保护作用做了深入的探索，应用结果表明，通过改进混气设备、增加安全装置并严格控制操作工艺，SO2可以用于镁熔体保护。一般认为SO2的保护机理是由于混合气体与镁熔体反应生成的多层复合保护膜而具有保护性。......
2025-09-29
-
高效抓取：机械手在工业用途优化中的应用详细阅读
可用于对机械手进行分类的影响因素大致为4个。图3.64模拟人手的机电机械手使用这些机械手已经使人形机器人及服务应用的研究和开发受益。图3.65三指机械手的调整选项即使使用最先进的技术，模块化的机械手仍然比人类的手更大，并且在抓取力方面比人手更困难。表3.13人造手的类型例如，用于外太空应用的DLR Dexhand旨在允许机器人也可使用供人类使用的工具。......
2025-09-29
-
CAE在推广和应用设计中的优势详细阅读
可是，事实上，却很少在国内发现有推广设计CAE的优秀事例。不从认识上消除这些担心，就难以在设计现场推广应用CAE，这也是没有引进设计CAE的一个原因。现在本田大量地采用了设计CAE，实现了从KKD设计到设计CAE的转变。在领导人员认识和理解了设计CAE的重要性和优越性以后，问题就成功了一半。特别要注意采用那些设计人员易于熟悉的工具，如与CAD系统集成的CAE工具。......
2025-09-29
-
使用夹子在SolidWorks中创建零件模型详细阅读
图17.3.1 零件模型及模型树Step1.新建模型文件。选择下拉菜单命令，系统弹出“创建草图”对话框；选取XY基准平面为草图平面，单击按钮，进入草图环境，绘制图17.3.2所示的草图1；单击按钮，退出草图环境。在绘图区选取YZ基准平面为草图平面，添加图17.3.3所示的草图2。选择图17.3.10a所示的边链为边倒圆参照，并在文本框中输入值2，完成边倒圆特征2的添加。Step8.添加图17.3.10b所示的边倒圆特征2。......
2025-09-29
-
应用实例：6.4冶金工业中的优秀案例详细阅读
热喷涂技术在冶金机械中的应用历史较长，技术比较成熟。近年来，随着冶金制造技术水准的不断提高，速度、效率要求越来越高，新的涂层材料、涂层制备工艺技术正在逐步扩展在冶金工业中的应用。钢铁冶金设备中热喷涂技术的应用见表6-7。表6-7 钢铁冶金设备中热喷涂技术的应用（续）1.高炉渣口、风口基体材料为纯铜或铸锡青铜，长期承受高温气体的冲蚀及熔渣、铁液的冲刷，主要破坏形式是烧蚀。该工艺技术镀锌生产中已普遍采用。......
2025-09-29
-
颗粒流基本方程简介详细阅读
将φ 乘以Boltzmann方程的两边，对整个颗粒脉动速度空间积分，获得φ 的输运方程。因此，可以通过假设颗粒的速度分布函数获得颗粒流的应力和能量通量等的表达式，或者用统计平均的办法建立各类守恒型方程来描述颗粒流的平均运动。因此，需要通过一定假设，建立泥沙颗粒相的本构关系。......
2025-09-29
相关推荐