采用分子混沌假设，并认为颗粒之间以二体碰撞为主。上述本构关系式由Gidaspow 针对气固两相流率先提出，在气固两相流模拟中获得了较广泛的应用。因此，上述本构关系严格地说，仅适用于速度梯度较小、颗粒近乎弹性的颗粒流。......
2025-09-29
验证颗粒流模型的可靠性
【摘要】：Bagnold 最先在同心圆筒间进行悬浮石蜡颗粒的剪切试验，颗粒直径为1.32mm，比重为1.05g/cm3;以水、酒精和甘油混合成不同比重的溶液来平衡颗粒的自重，当浓度C≥0.3 时，颗粒碰撞作用占优势，Bagnold实验用来验证本文的理论结果。当浓度C 从0.04 增加到0.35 时，两者之比从10减小到0.1，该浓度范围内的颗粒碰撞应力和脉动应力都很重要。
检验前述颗粒流理论的资料并不多，合适的有Bagnold (1954)、Savage和Sayed(1983)的试验资料，Campbell和Brenner(1985)的计算机模拟资料。
Bagnold (1954)最先在同心圆筒间进行悬浮石蜡颗粒的剪切试验，颗粒直径为1.32mm，比重为1.05g/cm3;以水、酒精和甘油混合成不同比重的溶液来平衡颗粒的自重，当浓度C≥0.3 时，颗粒碰撞作用占优势，Bagnold实验用来验证本文的理论结果。Savage和Sayed(1983)在同心圆筒中对干燥颗粒进行了高速剪切试验，颗粒体积比浓度的变化范围为0.44～0.54。试验采用了两种不同颗粒，其中聚苯乙烯圆球颗粒的直径为1mm，比重为1.05g/cm3;玻璃球的直径为1.08mm，比重为2.97g/cm3。碰撞恢复系数e是颗粒流应力表达式中的重要参数，Bagnold (1954)、Savage和Sayed (1983)的试验都没有测量e值，Campbell和Brenner(1985)用计算机分别模拟了e取0.6和0.8时的情况。
用式(3-42)和式(3-43)分别计算无量纲形式的碰撞正应力和碰撞切应力随浓度变化曲线，计算中依次取e=0.6、0.8、0.9、0.95四个值。图3-3给出了理论预测与试验及计算机模拟结果的比较。由图可见，随着浓度增加，碰撞应力都单调增加。碰撞正应力的试验结果都落在式(3-43)取e=0.8～0.95的范围;e=0.95时的碰撞切应力的理论曲线通过Savage和Sayed的点群中央，e=0.6的理论曲线与Bagnold的试验资料一致。总体上，尽管由于试验条件各不相同，呈现出试验数据点有些散乱，但从图3-3可以看出碰撞应力的理论结果与试验资料的符合程度令人满意。
图3-4为式(3-46)和式(3-47)预报的碰撞应力与脉动应力之比随浓度的变化曲线，图中也绘出了Lun et al. (1984)的理论模型及Campbell和Gong (1986)的计算机模拟结果。需要说明的是，Campbell和Gong(1986)的计算机模拟结果是关于二维粗糙圆盘模型的，式(3-46)和 (3-47)及Lun et al. (1984)是关于光滑圆球模型的，可能会存在一些差别。由图可见，式 (3-46)和式 (3-47)的预报曲线与Lun et al.(1984)的理论曲线非常接近，在体积比浓度C＜0.3时，两者都高于计算机模拟的结果。总体上，理论曲线给出了与计算机模拟结果相同的变化趋势。另外，图中碰撞恢复系数e的取值范围为0.4～1.0，可见e的取值对计算结果影响不大。(https://www.chuimin.cn)
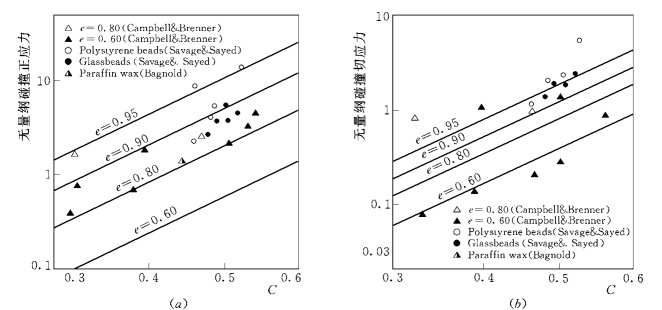
图3-3 无量纲碰撞正应力、碰撞切应力随浓度的变化及与试验和计算机模拟的比较
根据图3-4中的理论曲线，当颗粒体积比浓度C≤0.04时，颗粒脉动应力与碰撞应力之比大于10，即脉动应力占优势;当C≥0.35时，情况则正好相反，脉动应力与碰撞应力之比小于0.1，颗粒的碰撞作用占优势;在C=0.17时，两者差不多相等。当浓度C 从0.04 增加到0.35 时，两者之比从10减小到0.1，该浓度范围内的颗粒碰撞应力和脉动应力都很重要。该颗粒脉动应力和碰撞应力之比随浓度的变化关系，为颗粒相应力应变本构关系的简化提供了依据，也为高含沙水流与一般挟沙水流的划分初步提供了一个标准。
相关文章
- 详细阅读
-
数值模型验证：探索真实性详细阅读
Ccond=0.000 1时小流量和设计流量工况下离心泵扬程随有效空化余量变化的非定常数值计算结果与试验结果的比较如图2.6所示。表2.2NPSHc计算值与试验结果的比较在本书的离心泵空化流动数值模拟中，质量输运空化模型的凝结项经验系数取0.000 1进行数值计算。图2.7列出了小流量下NPSHa=1.0m和设计流量下NPSHa=1.6m时，3个不同凝结项经验系数所对应的叶轮内空泡体积率分布。......
2025-09-29
-
空化模型及其在均相流模型中的应用详细阅读
采用均相流模型中的质量输运空化模型，形式［141］如下：式中，分别表示质量蒸发速率和质量凝结速率；αν为空泡体积分数；ρν为汽体密度，其值为0.554 kg/m3。质量输运空化模型的质量蒸发速率和质量凝结速率，大多数为在Rayleigh-Plesset方程的基础上推导出来的，其形式为：式中，Rb为空泡平均半径，其值为10-6 m；ρl为液体密度，其值为997 kg/m3；pν为饱和蒸汽压力，其值为3 574 Pa；S为液体的表面张力；μ为液体的动力黏性系数。......
2025-09-29
-
使用3D PTV测量明渠均匀流颗粒运动规律的详细阅读
Dupont et al.采用立体摄像的3D PTV测量了0.6cm3空腔内晶体生长过程中颗粒三维运动的轨迹，作者只论证了该系统的可靠性，还没有颗粒运动规律的研究成果。本节介绍采用3D PTV试验研究明渠均匀流的颗粒运动规律，揭示出颗粒纵向平均速度符合对数分布规律，颗粒垂向的浓度分布符合Rouse方程。在近壁流区，颗粒纵向和垂向脉动速度的概率密度偏离正态分布，横向则接近正态分布。......
2025-09-29
-
颗粒污泥的性质分析详细阅读
成熟的颗粒污泥，VSS/SS一般为7%～80%，但根据废水性质其范围可在30%～90%。一般来说，反应器沿高度的群落演替遵循9.3.5中所述规律，而单一颗粒污泥的生物构成遵循生物代谢规律，即产酸细菌主要在颗粒表面，产甲烷细菌主要在颗粒内部。......
2025-09-29
-
类杆流活性聚能侵彻体释能模型探析详细阅读
图3.5类杆流活性聚能侵彻体化学能分布式释放过程虽然各微元速度梯度较类射流活性聚能侵彻体明显更小，但类杆流活性聚能侵彻体在运动及成形过程中不断拉伸延长，在t2时刻，长度为L2。在继续拉伸过程中，类杆流活性聚能侵彻体逐渐形成，整体密度降低，且由外至内、由头部至尾部，密度均逐渐下降。在空间尺度上，类射流活性聚能侵彻体不断拉伸、运动。......
2025-09-29
-
随机森林模型的原理详解详细阅读
另外，随机森林法可以评价各种指标的重要程度。装袋算法通过自助抽样法有效地提高了随机森林算法的准确度。Breiman在1984年提出的分类回归树是一种不稳定的学习算法，因此CART方法与装袋算法结合就形成了随机森林算法，可以提高模型预测准确率。随机森林模型中某一特征的重要性，是所有决策树得到的该特征重要性的平均值。......
2025-09-29
-
验证网络性能的方法详细阅读
图9-1实验测试平台和演示器设置基于测试平台，我们在软件定义的C-RoFN中实验性地设计并验证了MSO的服务。功能请求消息负责定期查询OF-BVOS关于当前状态的监视。此外，在选择目的地之后，CSO策略仅考虑光网络资源并以最小跳数计算路径。GES部分地扩展了BBU中的负载均衡和光网络中的平均跳跃性能，并将它们明显地转化为整体资源利用率的提高和路径配置响应的增强。图9-3算法性能比较......
2025-09-29
相关推荐