这些试验中的浓度和剪切率等参数都在较大范围内变化，可以验证前述颗粒相模型的预测性能。表3-2中列出了详细的试验条件。......
2023-06-22
如何进行简单剪切流操作？
【摘要】：在简单剪切流条件下，考虑式与式 之比、式 与式 之比有:3.2.4.2碰撞耗散率3.2.4.2碰撞耗散率在简单剪切流下，式简化为:由上式可见，在简单剪切流下，稠密气体分子动理学方法获得的碰撞耗散率与流场剪切率无关，随颗粒浓度的增加而增加，并与颗粒脉动能的3/2次方成正比。在简单剪切流下，平均速度的相对速度差与流场中的平均流速梯度有关，脉动速度的相对速度差在各个方向幅值相同，那么有:式中:B 是待定参数。
3.2.4.1 应力关系
在简单剪切流下，考虑笛卡尔直角坐标系，设平均流动沿着x 方向，平均流速梯度只沿y 向存在，即:
由式(3-23)可以简化得到颗粒相的脉动应力和切应力:
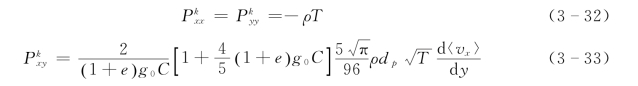
由式(3-19)和式(3-23)获得颗粒相的碰撞正应力和切应力:
由式(3-25)获得颗粒相的总正应力和总切应力:
在简单剪切流条件下，类比气体分子运动论中的平均自由程方法，也可以获得颗粒相脉动应力的表达式，从而建立应力应变的本构关系(王光谦，1989):
式中:l为平均自由程，考虑浓度修正的表达式如下:
从而获得基于平均自由程方法的脉动应力分量:
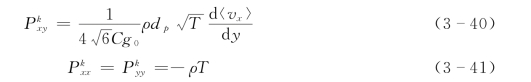
相应地，将上述脉动正应力和脉动切应力表达式带入到碰撞应力公式，可以获得基于平均自由程方法的简单剪切流碰撞应力分量:
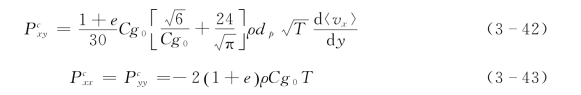
虽然上述两种方法繁简各异，但所给出的脉动正应力和碰撞正应力分别相同，在切应力上存在稍许差别。为比较两种方法结果的差异，将式 (3-33)与式 (3-40)进行比较有:
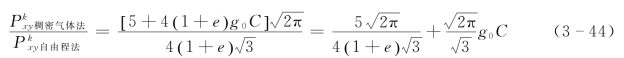
用式(3-44)计算两种方法所给出的脉动切应力比值，如表3-1和图3-2所示，其中，颗粒径向分布函数g0如下(Carnahan和Starling，1969):
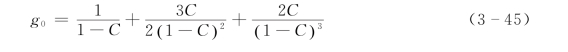
表3-1 两种方法所预报的脉动切应力比较
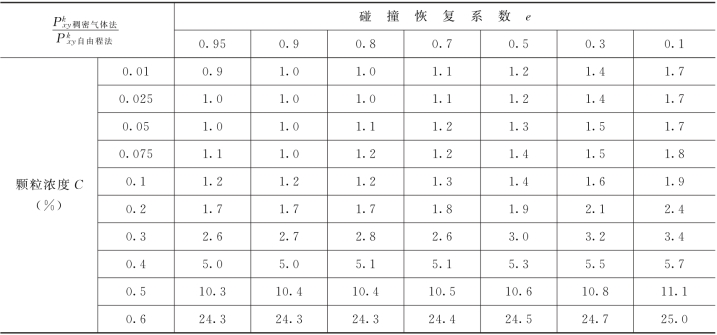
图3-2 两种方法所预报的脉动切应力之比随浓度变化
由该表可见，碰撞恢复系数e的取值对不同方法计算的脉动切应力值影响不大;随着浓度的增大，两者之间差别逐渐明显，当C＞0.4时，稠密气体动理学方法给出的结果已是自由程法的5倍以上。
颗粒流模型能够描述颗粒相应力的颗粒脉动和粒间碰撞等生成机制，因此能够给出脉动应力和碰撞应力随流动条件的变化，说明不同流动条件下各应力组成的相对重要性。一般而言，在低浓度下，颗粒的脉动应力起控制作用;高浓度下，粒间碰撞起主导作用。在简单剪切流条件下，考虑式(3-40)与式 (3-42)之比、式 (3-41)与式 (3-43)之比有(王光谦，1989):
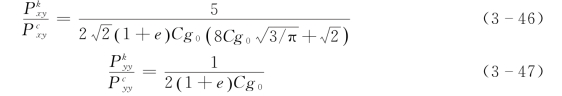
3.2.4.2 碰撞耗散率
在简单剪切流下，式(3-22)简化为:
由上式可见，在简单剪切流下，稠密气体分子动理学方法获得的碰撞耗散率与流场剪切率无关，随颗粒浓度的增加而增加，并与颗粒脉动能的3/2次方成正比。
通过平均自由程方法，假设碰撞耗散率与碰撞次数和每次碰撞的能量损失有关，也可以获得耗散率的表达式(王光谦，1989):
式中:ΔE 为颗粒每次碰撞的平均能量损失;N 为单位时间、单位体积中颗粒碰撞的总次数。
类比气体分子动理学理论，考虑颗粒浓度的影响，颗粒的碰撞次数N 为:
每次碰撞的平均能量损失ΔE 取决于颗粒的碰撞过程和颗粒的物理属性。假设颗粒碰撞主要是瞬时完成的二体碰撞，每个碰撞颗粒的脉动速度方向任意。在简单剪切流下，平均速度的相对速度差与流场中的平均流速梯度有关，脉动速度的相对速度差在各个方向幅值相同，那么有:
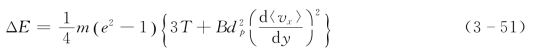
式中:B 是待定参数。
由式(3-50)和式(3-51)可得脉动能碰撞耗散率:
比较上述两种方法获得的脉动能碰撞耗散率，可以看到，式 (3-48)与式 (3-54)都含有与平均流速梯度无关的部分，该部分在形式上只是系数有差别、都与颗粒脉动能的3/2次方成正比。但是，式(3-54)反映了平均流速梯度 (或流场剪切率)的影响，且与剪切应力的剪切功在形式上相近。
有关泥沙研究进展的文章
- 详细阅读
-
如何进行下盖操作？- 实战教程详细阅读
选取图8.4.2a所示的曲面，选择下拉菜单命令；在操控板中单击“去除材料”按钮，定义实体化方向如图8.4.2a所示，。在绘图区选取图8.4.14所示的边线，选择下拉菜单命令，在操控板中输入距离值3.0。Step17.创建图8.4.21所示的拉伸特征──拉伸4。选择下拉菜单命令；选取DTM5基准平面为草绘平面，选取ASM_FRONT基准平面为参照平面，方向为；单击对话框中的按钮，绘制图8.4.24所示的截面草图；在操控板中选取深度类型为，按下“加厚草绘”按钮，输入值0.5。......
2023-06-26
-
如何进行定义放置操作？详细阅读
定义放置时首先选择坐标系，然后在原曲面内选择一个基准点。系统会创建从固定原点到指定基准点之间的向量，并使该向量与坐标系X轴对齐。具体操作步骤如下：打开源文件第5章∣5-7-2.prt，曲面如图5-82所示。3）选择的默认设置，勾选选项卡中的，系统将弹出如图5-83所示的选项。5）单击对话框中的按钮，完成定义放置展平面组的创建，如图5-85所示。图5-84 对话框图5-85 定义放置注1：与默认展平不同的是，定义展平需要两个基准点用以确定展平方向。......
2023-06-19
-
如何在模型空间中进行打印操作？详细阅读
在模型空间进行页面设置，以在A3图纸上打印如图3-21所示的图形。以“A3样板.dwt”样板文件开始新建文件，新文件的名称为“Drawing1.dwg”。确认为“模型”，然后单击按钮。图7-21对话框在下拉列表框中选择，对话框暂时隐藏。根据命令行提示分别捕捉外图框的对角点，以确定打印区域，自动返回对话框。单击工具栏上的按钮，预览效果合适，在右键菜单中选择。......
2023-06-21
-
如何使用续流二极管进行浪涌抑制？详细阅读
二极管还具有检波功能。为了便于声波等的传送，常把声波承载在一种频率很高的调制波上面，这种调制波称为载波。图2-20中的二极管就可以起到使这种冲击电流不流经开关的作用，这种作用称为浪涌抑制，这种二极管也常称为续流二极管。在续流二极管的保护下，继电器的触点可以避免浪涌电流的冲击而正常工作。应该指出，当选择续流二极管时，其反向耐压应留有充分的余量。......
2023-06-25
-
如何进行铸钢件组焊操作详细阅读
7.焊接过程中对尺寸进行检查焊接过程为了确保厚壁结构铸钢件组装后的中心位置、尺寸、垂直度、相对扭曲度，两构件之间的平行度和中心尺寸，除了焊前对装配尺寸进行检查外和焊接过程采取的变形监控措施，还应该在打底焊、坡口焊至1／3或1／2深度后分别进行尺寸和MT（干粉）检测，以便随时可以对焊接过程结构尺寸及变形情况和焊接质量进行控制，发现问题及时采取措施改正。......
2023-06-28
-
如何使用SolidWorks进行模型修剪和抽详细阅读
选取图21.11.4a所示的模型体为修剪的目标体，单击鼠标中键后，选取ZX基准平面为刀具体，可通过“反向”按钮调整修剪方向，箭头指向被修剪的部分。选择下拉菜单命令，在“抽壳”对话框区域的下拉列表中选择选项，选择图21.11.6所示的面为移除面，在区域的文本框中输入值2；在区域的文本框中输入0.2；其他参数采用系统默认设置值。Step4.创建图21.11.5所示的抽壳。图21.11.5 抽壳图21.11.5 抽壳图21.11.6 定义移除面图21.11.6 定义移除面Step5.创建图21.11.7b所示的边倒圆特征1。......
2023-06-22
-
学习如何绘制简单直线详细阅读
根据相关直线或相关方程就可由x插补延长系列y。按照这一准则确定的相关直线称最小二乘法准则，由此求得的相关方程称为y倚x的回归方程，相应相关直线也称为回归线。将式、式代入式得y倚x的回归方程——x、y系列的模比系数；r——相关系数，表示x、y之间线性相关的密切程度。数理统计中经过研究，由式估计回归方程的误差称δy为y倚x回归线的均方误，式中各符号含义同前。......
2023-06-21
相关推荐