以两个变量为例进行讨论。这种关系x与y的关系点杂乱无章，如图X3.15所示。相关关系，指两个变量x与y之间的关系介于完全相关和零相关之，这种关系x与y的关系点呈带状分布趋势，如图X3.16所示。图X3.15零相关示意图图X3.16相关关系示意图直线相关；曲线相关例如，流域年径流深与年降水量之间的关系，就是相关关系。......
2025-09-29
颗粒流本构关系的探讨
【摘要】：采用分子混沌假设，并认为颗粒之间以二体碰撞为主。上述本构关系式由Gidaspow 针对气固两相流率先提出，在气固两相流模拟中获得了较广泛的应用。因此，上述本构关系严格地说，仅适用于速度梯度较小、颗粒近乎弹性的颗粒流。
3.2.3.1 碰撞量的本构关系
考虑大小相等的光滑圆球颗粒的非弹性碰撞。采用分子混沌假设，并认为颗粒之间以二体碰撞为主。设参与碰撞的颗粒1和颗粒2，趋近于碰撞点时分别具有速度v1i和v2i，碰撞瞬间完成时的速度分别为v′1i和v′2i，碰撞时颗粒中心分别位于x1i、x2i。那么碰撞前后颗粒1、2之间的相对速度依次为:
选取表征颗粒非弹性的碰撞恢复系数e，并认为e为物性参数，与流动条件无关，那么碰撞前后的速度关系和能量变化为:
选取表征颗粒非弹性的碰撞恢复系数e，并认为e为物性参数，与流动条件无关，那么碰撞前后的速度关系和能量变化为:
结合上述关系式，考虑到所有函数均在点xi处取值，则守恒方程中的碰撞应力张量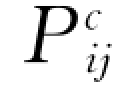
、脉动能碰撞传导通量
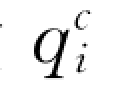和脉动能碰撞耗散源项γc依次为:
结合上述关系式，考虑到所有函数均在点xi处取值，则守恒方程中的碰撞应力张量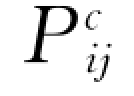
、脉动能碰撞传导通量
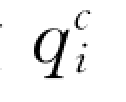和脉动能碰撞耗散源项γc依次为:
上述方程中，碰撞应力张量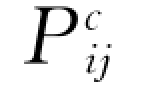
表达式与稠密气体分子动理学中的相应结果具有相同的结构形式(Chapman和Cowling，1970)，唯一区别在于其系数中出现了反映颗粒非弹性影响的 (1+e)/2。如果单颗粒速度分布函数f 的一级近似采用正态分布函数f(0)(Maxwell分布)，按照稠密气体分子动理学的有关求解步骤，上式将给出与稠密气体分子动理学理论近乎相同的积分结果。王光谦(1989)基于这样的考虑，直接类比引用了气体分子动理学理论中的相应成果，获得了
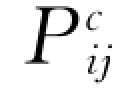的二阶近似式;Ding和Gidaspow (1990)依照稠密气体分子动理学理论的求解步骤，获得了相同的结果，表达式如下:
上述方程中，碰撞应力张量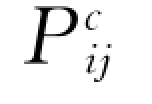
表达式与稠密气体分子动理学中的相应结果具有相同的结构形式(Chapman和Cowling，1970)，唯一区别在于其系数中出现了反映颗粒非弹性影响的 (1+e)/2。如果单颗粒速度分布函数f 的一级近似采用正态分布函数f(0)(Maxwell分布)，按照稠密气体分子动理学的有关求解步骤，上式将给出与稠密气体分子动理学理论近乎相同的积分结果。王光谦(1989)基于这样的考虑，直接类比引用了气体分子动理学理论中的相应成果，获得了
的二阶近似式;Ding和Gidaspow (1990)依照稠密气体分子动理学理论的求解步骤，获得了相同的结果，表达式如下:
式中:T= 〈ViVi〉/3为颗粒相温度;δij为二阶单位张量;Sij为无散应变率张量，定义为:
式中:T= 〈ViVi〉/3为颗粒相温度;δij为二阶单位张量;Sij为无散应变率张量，定义为:
沿用稠密气体分子动理学中的求解步骤，Ding和Gidaspow (1990)利用正态分布函数作为一级近似，还得到了脉动能碰撞传导通量和脉动能碰撞耗散源项的积分计算结果:
沿用稠密气体分子动理学中的求解步骤，Ding和Gidaspow (1990)利用正态分布函数作为一级近似，还得到了脉动能碰撞传导通量和脉动能碰撞耗散源项的积分计算结果:(https://www.chuimin.cn)
3.2.3.2 脉动量的本构关系
3.2.3.2 脉动量的本构关系
上一小节得到了碰撞应力、脉动能碰撞传导通量和脉动能碰撞耗散源项的理论结果，其中含有颗粒脉动速度的二阶相关和三阶相关。沿用稠密气体分子动理学的方法，Gidaspow (1994)获得了颗粒相脉动应力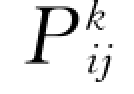
和脉动能脉动传导通量
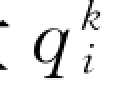本构关系:
上一小节得到了碰撞应力、脉动能碰撞传导通量和脉动能碰撞耗散源项的理论结果，其中含有颗粒脉动速度的二阶相关和三阶相关。沿用稠密气体分子动理学的方法，Gidaspow (1994)获得了颗粒相脉动应力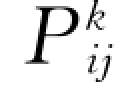
和脉动能脉动传导通量
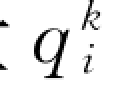本构关系:
结合碰撞应力和脉动能碰撞传导通量的本构关系式，得到颗粒相总应力和脉动能总传导通量的本构关系:
结合碰撞应力和脉动能碰撞传导通量的本构关系式，得到颗粒相总应力和脉动能总传导通量的本构关系:
式中
式中
上述本构关系式由Gidaspow (1994)针对气固两相流率先提出，在气固两相流模拟中获得了较广泛的应用。注意到上述稠密气体分子动理学方法，仅适合于流场速度梯度较小的条件。推广到颗粒流情形，还需要假定颗粒近乎弹性(1-e→0)。因此，上述本构关系严格地说，仅适用于速度梯度较小、颗粒近乎弹性的颗粒流。
上述本构关系式由Gidaspow (1994)针对气固两相流率先提出，在气固两相流模拟中获得了较广泛的应用。注意到上述稠密气体分子动理学方法，仅适合于流场速度梯度较小的条件。推广到颗粒流情形，还需要假定颗粒近乎弹性(1-e→0)。因此，上述本构关系严格地说，仅适用于速度梯度较小、颗粒近乎弹性的颗粒流。
相关文章
- 详细阅读
-
弯矩、剪力与分布荷载集度的关系探讨详细阅读
实际上，在载荷集度、剪力和弯矩之间存在着普遍的微分关系。由此表明弯矩图的变化形式与载荷集度q的正负值有关。表6-1梁上荷载和剪力图、弯矩图的关系利用梁的剪力图、弯矩图与荷载之间的规律作梁的内力图，通常称为简捷法作剪力图、弯矩图。梁的端截面、集中力、集中力偶的作用截面、分布荷载的起止截面都是梁分段时的界线截面。......
2025-09-29
-
使用3D PTV测量明渠均匀流颗粒运动规律的详细阅读
Dupont et al.采用立体摄像的3D PTV测量了0.6cm3空腔内晶体生长过程中颗粒三维运动的轨迹，作者只论证了该系统的可靠性，还没有颗粒运动规律的研究成果。本节介绍采用3D PTV试验研究明渠均匀流的颗粒运动规律，揭示出颗粒纵向平均速度符合对数分布规律，颗粒垂向的浓度分布符合Rouse方程。在近壁流区，颗粒纵向和垂向脉动速度的概率密度偏离正态分布，横向则接近正态分布。......
2025-09-29
-
中国传统道器观：探讨道与器之间的关系详细阅读
在中国古代哲学中，道器关系一直是有争议的话题。“形而上者谓之道，形而下者谓之器”——这句两千多年前的《易经·系辞上》中的名言是传统道器观的重要思想和理论来源。同时还认为，形而上的道与形而下的器“统之乎一形”，均由阴阳一气所派生，道即在器之中或称道不离器，他的观点使“器以载道”成为当代人认识和解释道器关系的基础。......
2025-09-29
-
颗粒污泥的性质分析详细阅读
成熟的颗粒污泥，VSS/SS一般为7%～80%，但根据废水性质其范围可在30%～90%。一般来说，反应器沿高度的群落演替遵循9.3.5中所述规律，而单一颗粒污泥的生物构成遵循生物代谢规律，即产酸细菌主要在颗粒表面，产甲烷细菌主要在颗粒内部。......
2025-09-29
-
探讨径流量法中的相关系数：从理论到实践的考量详细阅读
对于干旱地区，年径流量与年降水量之间的关系不太密切，难以利用这个关系来展延年径流量系列。当设计站的实测年径流量系列过短，不足以建立年降水量与年径流量的相关关系时，也可用月降水量与月径流量之间的关系来展延月、年径流量系列。可以使月降雨量和月径流量之间的关系得到改善。有了经插补延长的年径流量系列，就可进行频率计算和年内分配计算，计算方法与有长期实测资料的完全相同。......
2025-09-29
-
时尚与个体的相互关系详细阅读
西美尔认为时尚外在于个体，时尚向个体展现的易变性是个体自我稳定感的对照，在对照中，个体的自我感意识到自身的相对持续性。随后西美尔对于时尚与个体、时尚与阶级之间关系的论述都是以上面两点为基础和前提的。西美尔认为，作为一种大众行为，时尚可以帮助个体克服羞耻感。在接下来关于时尚与个体关系的论述中，西美尔强调了个体的心理因素对于个人时尚和社会时尚的影响。......
2025-09-29
-
RC串联电路中电压的关系详细阅读
设RC串联电路的电流为i=Imsinωt根据纯电阻和纯电容交流电路中电流与电压的关系可以得到电阻两端的电压为uR=UmRsinωt电容两端的电压为同样有单片的位置色差方程电路总电压为u=uR+uC2.电压三角形做出以上电流、电压的相量图，如图5-47a所示。图5-47 RC串联电路相量图和电压三角形a）相量图 b）电压三角形由图5-47b可以得到RC串联电路中各电压之间的数量关系为要消位置色差，应有。......
2025-09-29
相关推荐